Лабораторная работа № 1. ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ ПРИ НАЛИЧИИ

Лабораторная работа № 1

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ ПРИ НАЛИЧИИ

ПОСТОЯННОЙ ПО ВЕЛИЧИНЕ СИЛЫТРЕНИЯ

Цель работы. Изучить основные закономерности колебаний наклонного маятника при наличии трения качения, определить коэффициент трения качения.

Приборы и принадлежности. Лабораторная установка «Наклонный маятник», набор шаров.

Краткие теоретические сведения

Колебания наклонного маятника относятся к свободным затухающим колебаниям, амплитуда которых из-за потерь энергии с течением времени уменьшается. Уравнение затухающих колебаний определяется свойствами колебательной системы и действующими в ней силами.

Сила трения качения. При качении без скольжения одного тела по поверхности другого возникает сила, препятствующая движению – сила трения качения. Сила трения качения возникает из-за деформации материалов катящегося тела и опоры, а также из-за разрыва образующихся молекулярных связей на площадке контакта. Трение качения, как и любое трение, всегда связано с необратимым процессом – превращением механической энергии в тепло.

Сила трения качения F _тр, действующая на катящееся по плоскости тело, прямо пропорциональна силе нормального давления N

,

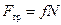где f – коэффициент трения качения. Коэффициент трения качения зависит от материала и состояния поверхностей соприкасающихся поверхностей, в довольно большом диапазоне скоростей не зависит от скорости катящегося тела. Для большинства материалов коэффициент трения качения при равных нагрузках значительно меньше, чем коэффициент трения скольжения, поэтому в технике по возможности стремятся заменить трение скольжения трением качения.

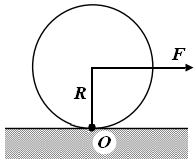Рис. 1

1. Уравнение колебаний наклонного маятника без учета силы трения качения. Рассмотрим шар массой m и радиусом R, который под действием силы F, приложенной к его центру, катится без проскальзывания по некоторой горизонтальной поверхности (рис. 1). Запишем основной закон динамики вращательного движения для катящегося шара относительно мгновенной оси вращения О

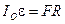, (1)

где 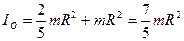– момент инерции шара относительно оси О; e – угловое ускорение центра масс шара.

Угловое ускорение связано с линейным ускорением соотношением

e = а / R.

Подставив его в уравнение (1), получим выражение, связывающее ускорение a центра масс катящегося шара и действующую силу F,

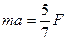. (2)

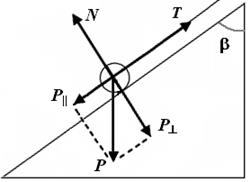
Далее рассмотрим движение шара, подвешенного на нити и катящегося по пластине, поверхность которой составляет угол наклона b к вертикали (рис. 2). Проанализируем силы, действующие на шар. Силу тяжести Р разложим на две составляющие, направленные перпендикулярно и параллельно наклонной плоскости:

Р _^= mg sinb, Р _|| = mg cosb.

Со стороны наклонной плоскости на шар действует сила реакции N. Сумма всех сил в направлении, перпендикулярном плоскости, равна нулю.

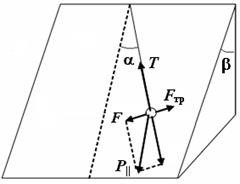
Силу Р _|| разложим так же на две составляющие, направленные вдоль нити и перпендикулярно ей (рис. 3). Сила F возвращающая шар в положение равновесия равна:

F = Р _|| sina = mg cosb sina, (3)

 

Рис. 2	Рис. 3

 

Уравнение движения (2) катящегося шара с учетом выражения (3) для возвращающей силы F будет иметь вид

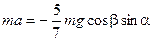. (4)

Знак минус означает, что возвращающая сила направлена в сторону, противоположную смещению от положения равновесия.

При малых углах отклонения, когда sina = a = x / L, где х – смещение шара от положения равновесия; L – длина маятника, выражение (4) можно записать

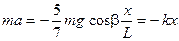, (5)

где

.

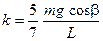Запишем уравнение движения (5) в дифференциальном виде, с учетом того, что ускорение есть вторая производная смещения по времени:

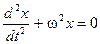или (6)

Уравнение (6) является линейным однородным дифференциальным уравнением второго порядка, аналогичным уравнению движения пружинного и математического маятника.

Решением дифференциального уравнения (6) является кинематическое уравнение движения вида

,

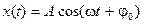согласно которому маятник совершает незатухающие гармонические колебания с амплитудой А, начальной фазой j₀, циклической частотой 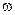и периодом колебаний

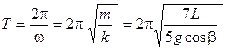. (7)

2. Уравнение колебаний наклонного маятника с учетом постоянной по величине силы трения качения. Уравнение движения (5) для катящегося шара с учетом силы трения качения F _тр будет имеет вид

ma = – kx ± F _тр, (8)

где знак минус у силы трения соответствует движению от положения равновесия, знак плюс – к положению равновесия, то есть сила трения постоянна по величине и переменна по направлению.

Запишем уравнение (8) в дифференциальной форме

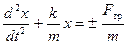. (9)

Фактически мы имеем два уравнения, описывающих движение шара в противоположных направлениях. Решения уравнений (9) имеют вид

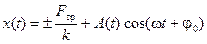. (10)

Период колебаний наклонного маятника, как и в случае отсутствия сил трения, равен

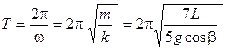. (11)

Закон убывания амплитуды A (t) определяется характером силы, вызывающей затухание. Для силы трения качения, не зависящей от скорости, можно считать, что амплитуда убывает по арифметической прогрессии, в противоположность случаю вязкого трения, когда сила трения прямо пропорциональна скорости и амплитуда убывает экспоненциально.

График затухающих колебаний x (t) наклонного маятника представлен на рис. 4 (сплошная линия). График зависимости амплитуды A (t) имеет вид прямой линии (рис. 4, пунктирная линяя).

3. Зависимость периода колебаний от угла наклона плоскости. Зависимость периода колебаний Т наклонного маятника от угла наклона плоскости b (11) можно представить в виде

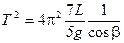. (12)

Если построенный по результатам эксперимента график зависимости Т ² от 1/cosb будет иметь вид прямой линии (рис. 5), то это будет подтверждением справедливости уравнения (12).

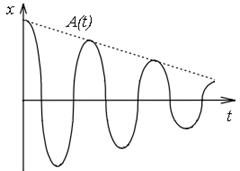Рис. 4

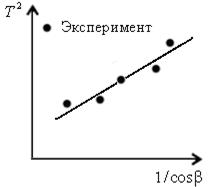Рис. 5

 

4. Определение коэффициента трения качения шара. Если маятник вывести из положения равновесия и отпустить, он будет катиться по наклонной плоскости по дуге окружности радиусом L (рис. 6). Амплитуда колебаний со временем уменьшается, так как энергия маятника расходуется на преодоление сил трения качения. На рис. 6 изображены положения шарика в начальный момент времени и через половину периода колебаний.

Изменение энергии маятника за половину периода равно разности потенциальных энергий шара в двух крайних положениях:

D Е = mg D h = mg D l cosb = mgL (cosa _m – cosa _{m 0}) cosb, (13)

где a _{m 0} и a _m – угол отклонения маятника от положения равновесия в начальный момент времени и через половину периода.

С учетом того, что при малых углах cosa » 1 – a²/2, выражение (13) можно переписать в виде

D Е = ½ mgL (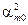 – 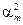) cosb, (14)

Работу сил трения качения за половину периода на пути, равном длине дуги окружности L (a _{m 0} + a _m), можно рассчитать следующим образом:

А _тр = F _тр L (a _{m 0} + a _m) = fN L (a _{m 0} + a _m), (15)

где сила нормального давления N = mg sinb (см. рис. 2).

Приравняв работу сил трения качения (15) изменению потенциальной энергии (14), получим уменьшение амплитуды колебаний за половину периода

a _{m 0} – a _m = 2 f tgb. (16)

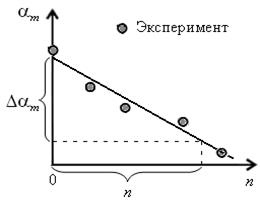Рис. 7

Из анализа выражения (16) следует, что изменение амплитуды колебаний одинаково для каждого полупериода. Следовательно, изменение амплитуды 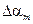за n целых периодов (колебаний) равно

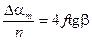, (17)

и зависимость амплитуды колебаний от числа колебаний a _m (n) имеет линейный характер (рис. 7).

Из выражения (17) можно получить расчетную формулу для коэффициента трения качения

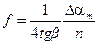, (18)

где изменение амплитуды 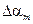выражено в радианах. Поскольку в лабораторной установке шкала для изме­рения углов проградуирована в градусах, то выражение (18) примет вид

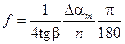. (19)

Значение 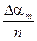может быть определено как угловой коэффициент прямой – графика зависимости a _m (n), построенного по результатам эксперимента (рис. 7).