1 метод: возведение обеих частей уравнения в одну и ту же степень.
2 метод: замена переменной.
3 метод: умножение обеих частей уравнения на одну и ту же функцию.
4 метод: применение свойств функций, входящих в уравнение.
Чаще всего при решении иррациональных уравнений применяют 1метод, то есть обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного. Следует не забывать, что уравнение-следствие наряду с корнями исходного уравнения может содержать и другие корни, которые называются посторонними. Поэтому после решения уравнения-следствия необходимо найти способ отсеять посторонние корни. Обычно это можно сделать при помощи проверки, которая в данном случае рассматривается как один из этапов решения.
Напомним, что при возведении обеих частей уравнения в чётную натуральную степень может получиться уравнение, не равносильное данному.
1 )Решим уравнение 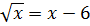 .
.
Решение. Возведём в квадрат обе части уравнения 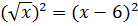 . Получим уравнение
. Получим уравнение 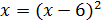 .
.
Обратите внимание: второе уравнение не равносильно исходному, так как первое уравнение имеет только один корень — 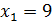 , а второе — два корня –
, а второе — два корня – 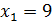 и
и 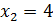 .
.
В этом случае второе уравнение называют следствием первого уравнения. Отметим, что второй корень является посторонним для исходного уравнения, так как при подставновке его в исходное уравнение получим неверное равенство.
Как видим, при возведении иррационального уравнения в натуральную степень могут появиться посторонние корни, поэтому проверка обязательна.
При решении иррациональных уравнений необходимо учитывать основные свойства иррациональных уравнений:
1. Если показатель радикала – чётное число, то подкоренное выражение должно быть неотрицательным, при этом значение радикала также является неотрицательным. Проще говоря, все корни чётной степени, входящие в уравнение, являются арифметическими, то есть если подкоренное выражение отрицательно, то корень лишён смысла; если подкоренное выражение равно 0, то корень также равен 0; если подкоренное выражение положительно, то значение корня – положительно.
2. Если показатель радикала – нечётное число, то подкоренное выражение может быть любым действительным числом. В этом случае знак радикала совпадает со знаком подкоренного выражения. Говоря другими словами, все корни нечётной степени, входящие в уравнение определены при любом действительном значении подкоренного выражения и в зависимости от знака подкоренного выражения могут принимать как неотрицательные, так и отрицательные значения.
А теперь давайте приступим к практической части нашего урока.
2) Решите уравнение 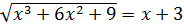 .
.
Решение. Отметим, что при  уравнение не имеет корней, так как правая часть нашего уравнения будет принимать отрицательные значения. А мы знаем, что значение корня не может быть отрицательным числом. Значит, нам будут подходить только корни больше либо равные 3.
уравнение не имеет корней, так как правая часть нашего уравнения будет принимать отрицательные значения. А мы знаем, что значение корня не может быть отрицательным числом. Значит, нам будут подходить только корни больше либо равные 3.
Итак, возведём в квадрат обе части уравнения 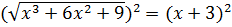 . Получим равносильное уравнение
. Получим равносильное уравнение 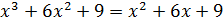 .
.
Перенесём все слагаемые из правой части уравнения в левую 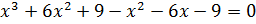 . Получим уравнение
. Получим уравнение 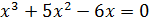 .
.
Теперь вынесем общий множитель х за скобки. Получим уравнение 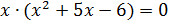 . В скобках квадратный многочлен разложим на множители.
. В скобках квадратный многочлен разложим на множители.
Имеем 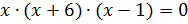 .
.
Чтобы данное уравнение равнялось 0, нужно чтобы хотя бы один из множителей равнялся 0.
Отсюда полученное уравнение имеет корни 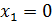 ,
, 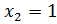 ,
, 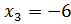 .
.
Вначале решения мы с вами оговаривали, что корни меньше –3 нам не подходят. Проверим, подходят ли корни 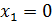 и
и 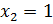 . Подставим их в исходное уравнение. При
. Подставим их в исходное уравнение. При 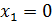 левая часть исходного уравнения равна
левая часть исходного уравнения равна 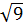 , а правая – 3. Имеем верное равенство. Значит,
, а правая – 3. Имеем верное равенство. Значит, 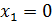 является корнем уравнения. При
является корнем уравнения. При 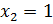 левая часть исходного уравнения равна
левая часть исходного уравнения равна 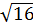 , правая – 4. Тоже имеем верное равенство.
, правая – 4. Тоже имеем верное равенство.
Следовательно, 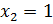 также является корнем уравнения.
также является корнем уравнения.
Ответ: 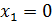 ,
, 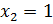 .
.
3). Решите уравнение 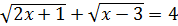 .
.
Решение. Возведём обе части уравнения в квадрат 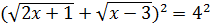 .
.
Получим равносильное исходному уравнение 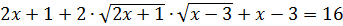 .
.
Приведём подобные члены и перенесём слагаемые без знака корня в правую часть уравнения 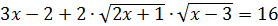 .
.
Получим уравнение 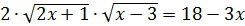 .
.
Возведём обе части получившегося уравнения в квадрат.
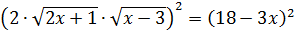
Получим уравнение 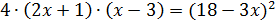 .
.
Раскроем скобки. Перенесём все слагаемые из правой части уравнения в левую. Приведём подобные.
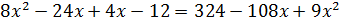 .
.
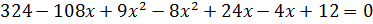 .
.
Получим уравнение 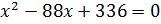 .
.
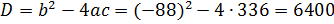
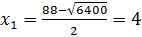 ,
, 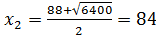 .
.
Последнее уравнение является следствием исходного уравнения. Вычислим его корни. Имеем 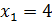 ,
, 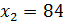 .
.
Выполним проверку.
При 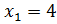 выражение
выражение 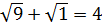 . Имеем верное равенство. Значит,
. Имеем верное равенство. Значит, 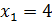 является корнем нашего уравнения.
является корнем нашего уравнения.
При 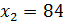 выражение
выражение 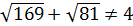 . Видим: имеем неверное равенство.
. Видим: имеем неверное равенство.
Следовательно, 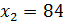 не является корнем нашего уравнения. Ответ:4.
не является корнем нашего уравнения. Ответ:4.