Критерий устойчивости Найквиста

И Найквиста.

С помощью этих критериев исследуется устойчивость САР в частотой области.

Частотный критерий Михайлова

Исходная информация – характеристическое уравнение разомкнутой или замкнутой системы

a_n sⁿ + a_n-1 s^n-1 + a_n-2 s^n-2 + …+ a₀ = 0.

Путём замены s на jw переходим к уравнению Михайлов

M(jw) = a_n (jw)ⁿ + a_n-1 (jw)^n-1 + a_n-2 (jw)^n-2 + …+ a₀ = P(w) + j Q(w),

где Р(w) – вещественная часть годографа Михайлова, чётная функция частоты; Q (w) – мнимая часть годографа Михайлова, нечётная функция частоты.

Критерий Михайлова формулируется следующим образом: система устойчива, если годограф Михайлова при изменении w от 0 до ¥ проходит в положительном направлении n квадрантов комплексной плоскости, начиная свое движение с точки а₀ положительной полуоси, и нигде не обращается в нуль.

Критерий Михайлова имеет и другую формулировку: система устойчива, если действительная и мнимая части годографа Михайлова обращаются в нуль поочерёдно, т.е. если корни уравнений

P(w) = 0 и Q(w) = 0

действительные и перемежаются, при w = 0 P(0) > 0, Q(0) > 0.

Пример: определить устойчивость системы, характеристическое уравнение которой

D(p) = 0,0057s³ + 0,58s² + s + 70.

Выполним подстановку s = jw и выделим вещественную и мнимую части годографа Михайлова

M(jw)= -j 0,0057w³ – 0,58w² j w +70 = (70 – 0,58 w²) + j (w - 0,0057 w³).

Для ряда значений частоты w вычислим вещественную

Р(w) = (70 – 0, 58 w²),

мнимую части кривой Михайлова

Q(w) = (w - 0,0057 w³)

и результаты расчётов сведём в таблицу, по данным которой можно построить кривую Михайлова. Для определения точек пересечения осей нужно решить уравнения Р(ω) = 0 и Q(ω) = 0. Однако целесообразно для построения графика использовать возможности MATLAB:

>> x=[0:1:20];

>> p=70-0.58*x.^2;

q=x-0.0057*x.^3;

>> plot(p,q),xlabel('P'),ylabel('Q') - рис. 6.3.

 

w	Р(w)	Q(w)
13.2 ¥	55,5 –28 -31 -60,5 –¥	4,29 4,3 3.41 0,477 –4,24 –¥

 

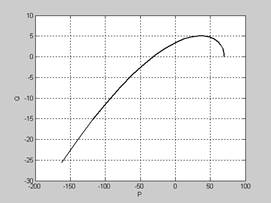
Рис. 6.3

Кривая Михайлова последовательно проходит три квадранта. Так как характеристическое уравнение исследуемой системы третьего порядка, то система устойчива.

Различные виды годографов представлены на рис. 6.4. Системе, находящейся на границе устойчивости, соответствует годограф, проходящий через начало координат, неустойчивой системе – кривая, проходящая через 1, 4 и 3 квадранты.

Рис. 6.4

Критерий устойчивости Найквиста

Это также частотный критерий, позволяющий судить об устойчивости системы, замкнутой единичной отрицательной обратной связью, по амплитудно-фазовой частотной характеристике разомкнутого контура. Предварительно требуется исследование устойчивости разомкнутой системы, как правило, по алгебраическим критериям. Для устойчивых и неустойчивых в разомкнутом состоянии систем формулировки критерия разные.

Если система устойчива в разомкнутом состоянии, то для устойчивости в замкнутом состоянии необходимо и достаточно, чтобы амплитудно -фазовая частотная характеристика разомкнутого контура не охватывала точку с координатами (-1, j0).

Для систем, неустойчивых в разомкнутых состояниях, критерий Найквиста имеет такую формулировку: если разомкнутая система неустойчива и имеет m корней в правой полуплоскости, то для устойчивости в замкнутом состоянии необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутого контура охватывала точку с координатами (-1, j0) m/2 раз.

Если система имеет местные обратные связи, то необходимо проверить устойчивость внутренних контуров любым критерием.

Пример: задана передаточная функция системы управления

Исследовать её на устойчивость.

Сделаем замену s = jω и найдём АФЧХ:

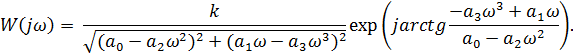
Кривая пересекает ось -1, если arctg φ = π. В этом случае

- a₃ω³ + a₁ω = 0. Следовательно, ω² = а₁ /a₃. При а₁ / а₃ = 1 ω = 1 и А(1) = k /(а₀ - а₂). Система может быть устойчивой или неустойчивой в зависимости от соотношения величин k, а₂, а₀.

Диаграмма Найквиста может быть построена в MATLAB с помощью функции nyquist([…],[…]) или nyquist(W).

Пример: построить годограф Найквиста для системы с передаточной функцией

В соответствии с критерием Гурвица эта система устойчива в разомкнутом состоянии. Исследуем её устойчивость в замкнутом состоянии:

>> W=tf([5],[1 3 3 1])

Transfer function:

---------------------

s^3 + 3 s^2 + 3 s + 1

>> nyquist([5],[1 3 3 1]) – рис. 6.5

Рис. 6.5

АФЧХ разомкнутой системы не охватывает точку с координатами

(-1, j0), поэтому замкнутая система устойчива.

6.4. Устойчивость систем с запаздыванием.

Отдельные звенья САР обладают “чистым” запаздыванием, которое сказывается в том, что система реагирует на входной сигнал не сразу, а по истечении некоторого постоянного времени t. Это обстоятельство учитывается введением звена чистого запаздывания с передаточной функцией

W(s) = exp (- t s),

а структурная схема системы показана на рис. 6.6.

Рис. 6.6

Передаточная функция разомкнутой системы

W_P (s) = W₀ (s) exp (- ts).

Система без запаздывания (t = 0) называется предельной.

Частотные характеристики системы с запаздыванием и без него определяются, соответственно, выражениями

W_P (jw) = W₀ (jw) exp (- t jw) =A(ω)exp[j(φ(ω)-ωτ)];

W_P (jw) = W₀ (jw)=A(ω)exp[jφ(ω)].

Отсюда видно, что для построения частотного годографа системы с запаздыванием следует построить годограф системы без запаздывания (предельной системы) и каждый вектор этого годографа повернуть по часовой стрелке на угол wt. Последний возрастает как при увеличении w, так и t.

Для некоторого значения t = t₀ и w = w_p годограф пройдёт через точку (-1, j0), и, следовательно, АСР будет находиться на границе устойчивости (рис. 6.7). Значения t₀ и w_p определяются из уравнения

W_p (jw_p) = W₀ (jw_p) exp (-jw_p t₀) = -1.

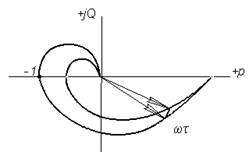
Рис. 6.7

Пример: система состоит из апериодического звена первого порядка с передаточным коэффициентом к > 1, постоянной времени Т и звена запаздывания с постоянной времени t. Определить предельное время запаздывания t₀, при котором система устойчива.

Модуль передаточной функции

W_P (jw_p) = mod W₀ (jw_p) = 1

или

к² = 1 + w_p² Т².

Отсюда

w_p² = (к² – 1)/ Т².

Аргумент передаточной функции

arg W_p(jw_p) = arg W₀ (jw_p) - w_pt₀ = -j - w_pt₀ = -p

или

t₀ = (p-j) / w_p,

где j = - arg W₀(jw_p) = arc tg (w_p T).

При t < t₀ система устойчива.

Если к = 7, Т = 100 с, t = 20 с, то w_p = 0, 085 с^-1, А(w_p) = 0,82 < 1 и система устойчива. Предельное время запаздывания t₀ = 25 с.

 

6.5. Влияние параметров системы на её устойчивость.

Диаграмма Вышнеградского. Границы устойчивости.

Для исследования влияния различных параметров системы на её устойчивость разработаны специальные методы, позволяющие облегчить их исследование. Рассмотрение влияния параметров на устойчивость системы может производиться двумя основными методами:

- путём анализа перемещения корней характеристического уравнения системы в плоскости корней – метод корневого годографа;

- путём анализа числа корней характеристического уравнения, лежащих в правой полуплоскости, в пространстве параметров системы – метод D;

- разбиения пространства параметров.