Тема 14. Статически неопределимые системы. Раскрытие статической неопределимости систем методом сил
Основные понятия и определения
В данной теме будут рассматриваться кинематически неизменяемые системы соединенных между собой балок и стержней, т.е. положение в пространстве всех элементов системы зафиксировано. Если элементы системы работают в основном на растяжение и сжатие, то эта стержневая система называется фермой, если элементы системы работают в основном на изгиб и кручение, то такую систему будем называть рамой.
Рамы и фермы могут быть плоскими, плоскопространственными и пространственными. У плоских систем продольные оси всех ее элементов расположены в одной плоскости. В этой же плоскости действуют все внешние силы (рис. 14.1а). У плоскопространственных систем оси элементов расположены в одной плоскости, а внешние силы действуют в плоскостях, перпендикулярных этой плоскости (рис. 14.1б). Конструкции, не относящиеся к выше перечисленным классам, называются пространственными (рис. 14.1в).
Рис. 14.1. Плоские, плоскопространственные и пространственные системы
Ограничения, накладываемые на возможные независимые перемещения свободного тела или на деформации его элементов, называются связями. Различают связи внешние и внутренние. Число внешних связей равно числу реакций опор, число внутренних связей – числу внутренних силовых факторов.
Под статически определимой системой понимают такую систему, для которой все реакции внешних связей могут быть определены из уравнений статического равновесия, а затем методом сечений могут быть определены все внутренние силовые факторы. Если реакции внешних связей и внутренние силовые факторы не могут быть определены из уравнений статики и методом сечений, то такая система называется статически неопределимой.
Если не удается из условия равновесия определить внешние связи (реакции опор), то систему называют внешне статически неопределимой, если нельзя методом сечений найти внутренние силовые факторы, система является внутренне статически неопределимой. Очевидно, что системы могут быть одновременно внешне и внутренне неопределимыми.
На рис. 14.2а изображена плоская статически определимая система (рама). Реакции находятся из уравнений статики, а внутренние силовые факторы во всех элементах – методом сечений (рис. 14.2б). На рис. 14.2в изображена та же рама, в которой добавлен шарнирно опертый стержень, работающий на растяжение – сжатие. Реакции внешних связей, как и в первом случае, находятся однозначно из уравнений равновесия. Однако определить внутренние силовые факторы методом сечений невозможно, т.к. при рассечении рамы произвольной плоскостью в сечении будет четыре неизвестных внутренних силовых фактора (рис. 14.2г), а для плоской рамы можно составить только три независимых уравнения статики. Следовательно, рама, рассмотренная на рис.14.2в, один раз внутренне статически неопределима.
Рис. 12.2. Статически определимые и неопределимые рамы
В рассмотренном примере сверх минимально необходимых для кинематической неизменяемости системы наложена одна «лишняя» связь. Всякую связь, наложенную сверх необходимых, называют дополнительной. Степень статической неопределимости системы равна числу дополнительных связей.
Метод сил
Наиболее распространенным методом раскрытия статической неопределимости системы в машиностроении является метод сил. В соответствии с данным методом система освобождается от дополнительных связей. Исходная система, освобожденная от всех дополнительных связей и с отброшенной системой внешних сил, называется основной системой. Действие на систему дополнительных связей заменяют неизвестными на данном этапе расчета силами и моментами. Величину этих сил и моментов подбирают таким образом, чтобы обобщенные перемещения характерных точек системы соответствовали ограничениям, наложенным на систему отброшенными связями. При таком способе раскрытия статической неопределимости неизвестными являются обобщенные силы. Отсюда и название метода – метод сил. Значит, раскрыть статическую неопределимость – определить обобщенные силы, которые заменяют воздействие на исходную систему отброшенных дополнительных связей.
Алгоритм раскрытия статической неопределимости рассмотрим на простом примере.
Пусть требуется провести расчет на прочность балки, изображенной на рис. 14.3. Будем считать, что изгибная жесткость балки постоянна по ее длине (EIос=const).
Рис. 14.3. Статически неопределимая балка
Решение.
1. Определяем степень статической неопределимости системы.
В жесткой заделке (слева по рисунку) возникают три реакции, в шарнирно-подвижной опоре – одна реакция. Итого четыре неизвестных. Для плоской системы можно составить три независимых уравнения статики. Значит, степень внешней статической неопределимости системы равна единице. Внутренне такая балка статически определима, т.к. в ее сечениях действуют два неизвестных силовых фактора (изгибающий момент и поперечная сила, а независимых уравнений статики можно составить три).
2. Выбираем основную систему.
Для этого необходимо отбросить какую либо дополнительную («лишнюю») связь. Таких основных систем может быть несколько, главное, чтобы после отбрасывания дополнительных связей система оставалась кинематически неизменяемой. В качестве примера на рис. 14.4 приведены два варианта возможных основных систем. В данном расчете в качестве основной выберем систему, показанную на рис. 14.4а.
Рис. 14.4. Основные системы статически неопределимой балки
3. Изображаем эквивалентную систему
Эквивалентная система представляет собой основную систему, на которую наложены все внешние нагрузки, действующие на исходную систему, а также прикладываются пока неизвестные обобщенные силы, заменяющие действие отброшенных дополнительных связей. Так как была отброшена одна связь (шарнирно – подвижная опора), то в точке В следует приложить силу X1, вертикально направленную (рис. 14.5). Направление (вверх или вниз) действия силы выбирается произвольно. Если оно выбрано неверно, то в процессе расчета будет получено значение силы с минусом. Полученная эквивалентная система отличается от исходной (рис. 14.3) тем, что в исходной системе вертикальное перемещение в точке В запрещено шарнирно - подвижной опорой, а в эквивалентной системе допускается.
Рис. 14.5. Эквивалентная система
4. Определение значения неизвестной силы X1.
Силу X1 подбирают из условия, чтобы перемещение точки В от совместного действия исходной системы внешних (Р) и неизвестной пока силы X1 было равно нулю, как и в исходной системе. Перемещение будем обозначать греческой буквой Δij с двумя индексами. Первый индекс (i) указывает на точку, перемещение которой рассматривается, и направление перемещения (например, i=1 – это значит, что рассматривается перемещение точки приложения силы X1 в направлении ее действия). Второй индекс указывает причину перемещения данной точки (например, j=P, т.е. перемещение рассматриваемой точки от действия силы Р). В данном случае на основании принципа независимости действия сил имеем
(14.1)
Первый индекс (1) указывает, что рассматривается перемещение точки приложения силы X1 (на рис.14.5 это точка В) в направлении ее действия. Второй индекс указывает, что рассматривается совместное действие внешней силы Р и пока неизвестной силы X1.
В соответствии с законом Гука, перемещение точки В от силы X1 представим в виде
,
где 
- перемещение точки В, где приложена сила X1, в направлении ее действия при X1=1.
Таким образом, условие (14.1) можно записать так
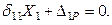(14.2)
Выражение (14.2) представляет собой каноническое уравнение метода сил. Коэффициент 
и свободный член 
по физическому смыслу представляют собой перемещения от действия некоторых обобщенных сил в рассматриваемой точке для статически определимой системы (эквивалентной системы). Они могут быть определены посредством интегралов Мора.
Так как при поперечном изгибе балки вкладом в перемещения поперечных сил можно пренебречь, то в интеграле Мора будем учитывать только изгибающий момент. Тогда имеем
В первом интеграле учтено, что перемещение определяется для единичной силы, которая заменяет силу X1. Подынтегральные выражения представляют собой произведение функций, одна из которых (М1) всегда линейна. Следовательно, для вычисления этих интегралов удобно использовать правило Верещагина. Для этого построим эпюры изгибающих моментов от силы Р (МР) и от единичной силы X1=1, как показано на рис. 14.6.
Рис. 14.6. Эпюры изгибающих моментов для консольной балки
В соответствии с правилом вычисления интегралов получим:
Подставляем найденные коэффициенты в уравнение (14.2) и находим неизвестную силу X1
Теперь, зная неизвестную ранее реакцию в шарнирно – подвижной опоре исходной системы X1, можно перейти от статически неопределимой исходной системы (рис.14.3) к абсолютно ей эквивалентной, но уже статически определимой системе, изображенной на рис.14.7. А так как это система статически определимая, то используя метод сечений не представляет труда определить внутренние силовые факторы во всех сечениях и решить задачу прочности.
Рис.4.7. Расчетная схема для эквивалентной системы
Учет свойств симметрии и кососимметрии
В реальных конструкциях достаточны часто встречаются рамы, симметричные в геометрическом отношении, когда есть ось симметрии, относительно которой правая часть рамы является зеркальным отражением левой. Оказывается, что геометрическая симметрия рамы позволяет существенно упростить решение задачи по раскрытию ее статической неопределимости при правильном выборе основной системы.
Введем понятия симметричной и кососимметричной нагрузки. Под симметричной нагрузкой будем понимать такую, при которой внешние обобщенные силы, приложенные к правой (относительно оси симметрии) части рамы, являются зеркальным отражением обобщенных сил, действующих на ее левую часть. Под кососимметричной (антисимметричной) понимают нагрузку, когда обобщенные силы, действующие на правую часть рамы, являются зеркальным отражением сил на левую часть, но с противоположным знаком. Так, на рис. 14.8а показан пример симметричной нагрузки, а на рис. 14.8б – кососимметричной.
Рис. 14.8. Симметричная и кососимметричная нагрузка симметричной рамы
Аналогично можно классифицировать и внутренние силовые факторы (рис. 14.9)
Рис. 14.9. Симметричные и кососимметричные внутренние силовые факторы
На данном рисунке видно, что к симметричным внутренним силовым факторам следует отнести изгибающие моменты Mx, My и нормальную силу N, а к кососимметричным силовым факторам крутящий момент Мк и поперечные силы Qx, Qy.
Рассмотрим геометрически симметричную раму (рис. 14.10а). Изображенная плоская рама трижды внешне статически неопределима. Выберем основную систему, разрезая раму по плоскости симметрии. Обозначим внутренние силовые факторы, действующие в плоскости рассечения для левой и правой частей рам Х1, Х2 и Х3 (рис. 14.10б).
В этом случае система канонических уравнений имеет вид:
Первое уравнение по физическому смыслу означает, что взаимное перемещение левого и правого сечений в разрезе в вертикальном направлении должно быть равно нулю при совместном действии внешней нагрузки и пока неизвестных обобщенных сил Хi. Второе уравнение соответствует взаимному перемещению в горизонтальном направлении, а третье – взаимный угол поворота по секущей плоскости должен также равняться нулю.
Рис. 14.10. Раскрытие статической неопределимости симметричной рамы
Построим эпюры для единичных силовых факторов, заменяющих обобщенные силы Х1, Х2 и Х3 (рис. 14.10в). Коэффициенты δij можно определять путем перемножения эпюр Mi и Mj по правилу Верещагина. Например, δ12 получаем перемножением эпюр М1 и М2. Учитывая вид эпюр и знаки внутренних силовых факторов, легко показать, что δ12= δ21= δ13= =δ31=0. Исходная система канонических уравнений примет вид
При симметричной внешней нагрузке также получим, что 
и из первого уравнения системы получаем Х1=0.
При кососимметричной нагрузке наоборот Δ2Р= Δ2Р=0, а значит из второго и третьего уравнений системы (однородные уравнения с ненулевым определителем) получим Х2=Х3=0.
ВЫВОД. У симметричной рамы в плоскости симметрии при симметричной внешней нагрузке обращаются в ноль кососимметричные силовые факторы, а при кососимметричной нагрузке – симметричные силовые факторы.
Указанная закономерность носит общий характер и облегчает решение многих статически неопределимых задач. Например, на рис. 14.11а изображена симметричная в геометрическом отношении рама, нагруженная кососимметричной нагрузкой. Если выбрать в качестве основной систему, у которой отброшены связи в одной из опор, то система окажется трижды статически неопределимой (рис. 14.11б) и для ее раскрытия придется решать систему из трех канонических уравнений. Если же за основную принять систему, полученную рассечением исходной рамы по плоскости симметрии, то симметричные внутренние силовые факторы будут равны нулю и единственной неизвестной величиной окажется вертикальная поперечная сила Х1 (рис. 14.11в). Значит, система один раз статически неопределима.
Рис. 14.11. Использование свойств симметрии и кососимметрии при выборе основной системы