Достаточное условие убывания функции.

Урок № 81-82.

Рабочий лист.

Предмет	Математика
Группа	№ 6 2 курс
Тема урока	Исследование функции с помощью производной.
ФИО преподавателя	Тимиршина Алия Мунзиловна
Где находится задание:
Учебник	Математика: учебник для учреждений нач.и сред. проф.образования/ М.И. Башмаков, Математика: задачник для учреждений нач.и сред. проф.образования/ М.И. Башмаков Алгебра и начала анализа: А.Н. Колмогоров
Ссылка	1. https://may.alleng.org/d/math-stud/math-st876.htm 2. https://www.belgtis.ru/images/obuch/pm/MatematikaZadachnikBashmakov.pdf 3. https://lib.maupfib.kg/wp-content/uploads/2015/12/Algebra_i_nachala_mat_analiz.pdf
Сроки выполнения задания	15.05.2021 до 17:00 часов
Как выполнять задание	Написать конспект, выполнить самостоятельную работу.
Домашняя работа	Задачник М.И. Башмакова стр.241 № 9.44 (5,6)
Обратная связь	Выполненные работы отправить личным сообщением ВК, при просмотре работы ставим лайки, чтобы знать кто присутствовал на уроке.
Как узнать отметку о выполненном задании	Оценки будут выставлены в личный журнал преподавателя и отправлены в беседу ВК.

Тема урока: Исследование функции с помощью производной.

Для чего нужно это исследование, спросите вы, если есть множество сервисов, которые построят график онлайн для самых замудренных функций? Для того, чтобы узнать свойства и особенности данной функции: как ведет себя на бесконечности, насколько быстро меняет знак, как плавно или резко возрастает или убывает, куда направлены "горбы" выпуклости, где не определены значения и т.п.

А уже на основании этих "особенностей" и строится макет графика - картинка, которая на самом-то деле вторична (хотя в учебных целях важна и подтверждает правильность вашего решения).

Начнем, конечно же, с плана. Исследование функции - объемная задача (пожалуй, самая объемная из традиционного курса высшей математики, обычно от 2 до 4 страниц с учетом чертежа), поэтому, чтобы не забыть, что в каком порядке делать, следуем пунктам, описанным ниже.

Алгоритм

1. Найти область определения. Выделить особые точки (точки разрыва).

2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.

3. Найти точки пересечения с осями координат.

4. Установить, является ли функция чётной или нечётной.

5. Определить, является ли функция периодической или нет (только для тригонометрических функций).

6. Найти точки экстремума и интервалы монотонности.

7. Найти точки перегиба и интервалы выпуклости-вогнутости.

8. Найти наклонные асимптоты. Исследовать поведение на бесконечности.

9. Выбрать дополнительные точки и вычислить их координаты.

10. Построить график и асимптоты.

Достаточное условие возрастания функции

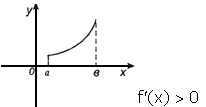
Если в каждой точке интервала (a, b) f'(x)>0, то функция f(x) возрастает на этом интервале.

Достаточное условие убывания функции.

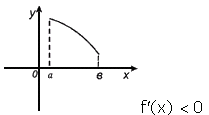
Если в каждой точке интервала (a, b) f'(x)<0, то функция f(x) убывает на этом интервале.

Определение:

x₀ называется критической точкой функции f(x), если

1) x₀ – внутренняя точка области определения f(x);

2) f'(x₀)=0 или f'(x₀) не существует.

Необходимое условие экстремума:

Если x₀– точка экстремума функции f(x), то эта точка является критической точкой данной функции.

Достаточное условие экстремума:

Если при переходе через точку x₀ производная функции меняет знак, то x₀ – точка экстремума функции f(x).

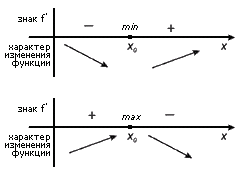
Примеры экстремумов:

 

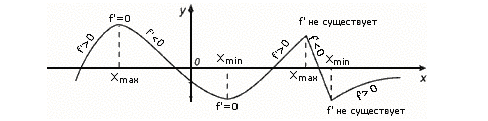
Пример 1.

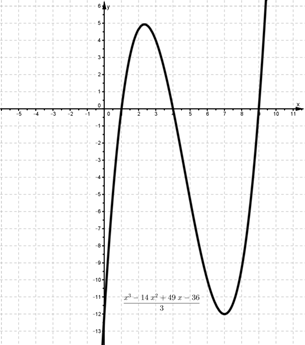
Исследовать функцию средствами дифференциального исчисления и построить ее график

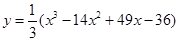
1.Область определения: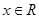

Функция существует при любом значении х.

2.Ни четная, ни нечетная.

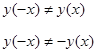
3.Нули функции:

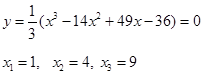
Имеем три точки пересечения с осью Ох.

4. Промежутки знакопостоянства:

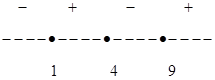
5. Промежутки возрастания функции:

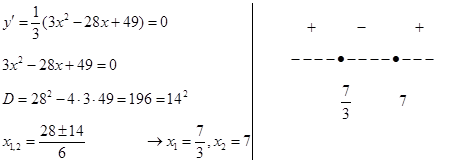
Получили промежутки возрастания функции: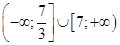

Промежутки убывания: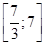

6. Выпуклость, вогнутость.

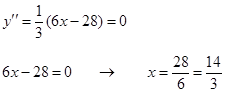
Нашли точку перегиба.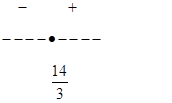

 

7.Наклонные асимптоты: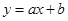

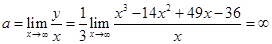
Наклонных асимптот нет.

 

Пример 2. Исследовать функцию у = 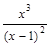и построить ее график.

Решение. 1) Функция у = 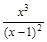определена всюду, кроме точки x=1. Отсюда область определения её: (–¥,1) È(1,+¥).

2) x=1 – точка разрыва функции.

Исследуем поведение функции в граничных точках области определения:

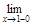f (x) = = +¥,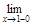

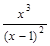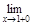f (x) =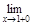 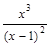= +¥, так как при х®1 знаменатель дроби является положительной бесконечно малой.

= = =+¥;

= = =–¥.

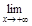
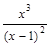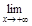
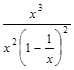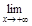
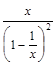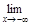
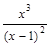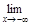
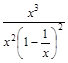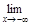
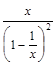3) Найдем точки пересечения графика функции с осями координат. При х = 0 получаем у = 0, т.е. график функции пересекает координатные оси в точке O(0,0).

4) Прямая х = 1 является вертикальной асимптотой графика функции.

Найдем наклонные асимптоты:

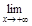
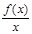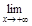
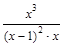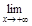
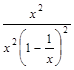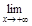
k= = = = = 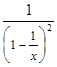1, т.е. k =1;

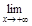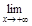
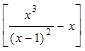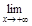
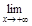
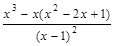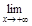
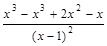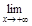
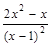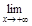
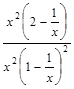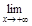
b = (f (x)– kx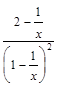) = = = = = = = = = =2,

т.е. b=2. Имеем уравнение правой наклонной асимптоты y = x +2.

Легко убедиться, что при x ®–¥ k и b имеют те же значения, т.е. уравнение левой наклонной асимптоты такое же y = x +2.

5) Найдем производную функции: y' = =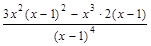

= = = .

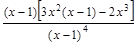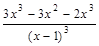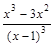Приравнивая y' к нулю, получим x ³–3 x ²=0, откуда имеем критические точки x ₁=0, x ₂=3. Для исследования знака производной в интервале (–¥;0), (0;3) и (3; +¥) на числовой оси отметим точки x =0, x =3 и х =1.

Определим знаки y' = 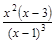в указанных интервалах.

 

Таким образом, в интервале (–¥;1) функция возрастает, в интервале (1,3) – убывает, в интервале (3,+ ¥) она возрастает. В точке x =3 функция имеет минимум: f (3) = 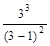= = 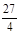6,75.

6) Найдем вторую производную:

y''= = = = =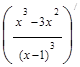

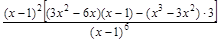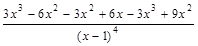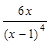= = , y''=0 при x =0. Так как знаменатель дроби (x –1)⁴>0 всегда (кроме x =1), то знак второй производной зависит лишь от числителя. При x <0 y''<0, при x >0 y''>0.

Точка x =0 является точкой перегиба. При x <0 кривая направлена выпуклостью вверх, так как y''<0, а при x >0 – выпуклостью вниз. В точке перегиба f (x) имеет значение f (0)=0.

Результаты наших исследований объединим в таблицу.

x	(–¥,0)		(0,1)		(1,3)		(3,+¥)
y'	+		+		–		+
y''	–		+		+		+
y	Ç	точка перегиба	È	не суще– ствует	È	min	È

Строим график функции, предварительно построив асимптоты и отметив точки минимума, перегиба и пересечения графика с осями координат.

 

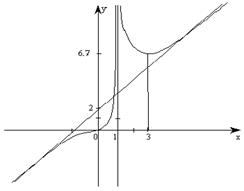
Задания для самостоятельного решения:

1. Провести полное исследование функции и построить её график

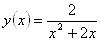
2. Исследуйте функцию с помощью производной и постройте ее график

3. Исследуйте функцию с помощью производной и постройте ее график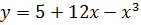

Домашнее задание: Задачник М.И. Башмакова стр.241 № 9.44 (5,6)