Дискретные и непрерывные случайные величины.

Исключение систематических погрешностей

Известные систематические погрешности можно исключить, либо за счет устранения источников погрешностей до начала измерений (профилактика погрешностей), либо путем введения известных поправок в результат измерения в процессе измерения. Профилактика погрешностей является наиболее рациональным спо­собом их снижения. Профилактику погрешностей измерения произ­водят путем регулировки, ремонта и поверки средств измерений. Снизить погрешность измерения можно, устранив влияние колеба­ния температуры (например, термоизоляцией), вибраций и т.п.

Поправка - это значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности. Путем введения поправки исключают, как правило, систематическую постоянную погрешность средств измерений.

При введении поправки уравнение измерения будет иметь вид

 

y=x+∆_c+∆_n,

 

где x - значение измеряемой величины;

∆_c - систематическая погрешность измерения;

∆_n - поправка.

Поправка численно равна значению систематической погрешности и противоположна ей по знаку ∆_n = - ∆_c

Полученное при измерении значение величины и уточненное путем введения в него необходимых поправок на действие систематических погрешностей называют исправленным результатом измерения. Неисправленный результат измерения - значение величины, полученное при измерении до введения в него поправок.

Одним из наиболее распространенных методов исключения систематических погрешностей в процессе измерения является метод замещения.

Для реализации этого метода сначала измеряют неизвестную величину (объект измерения размером х), в результате чего получают

 

х_си=х+∆_с,

 

где х_си - показания средства измерений.

Ничего не меняя в измерительной системе, устанавливают вместо объекта измерения размером х регулируемую меру (либо меру из набора) с размером х_м, подбирая такое ее значение, при котором достигается прежнее показание средства измерений, тогда

 

х_си= х_м+∆_c

 

Сопоставляя равенства получают значение неизвестной величины при х = х_м и определяют значение систематической погрешности

 

∆_с = х_си - х_м

Пример. При измерении диаметра цилиндрической детали штангенциркулем ШЦ-II-0,05 получен результат х_си = 25,75 мм.

 

Определить поправку, которую необходимо внести в показания прибора, используя набор плоскопараллельных концевых мер длины.

Такой же результат (25,75мм) получают при измерении штангенциркулем блока концевых мер размером х_м = 25,65 мм. Тогда х = 25,65 мм;

а систематическая погрешность штангенциркуля соста­вит, мм:

 

∆_с = 25,75 - 25,65 = 0,1мм.

 

Таким образом, поправка, которую необходимо ввести в пока­зания штангенциркуля, мм:

 

∆_n = - ∆_с = -0,1мм.

 

Универсальным методом исключения неизвестных постоянных систематических погрешностей является метод рандомизации. (random – случайный, выбранный наугад). Суть этого метода заключается в том, что одна и та же величина измеря­ется различными методами (приборами). Систематические погреш­ности каждого из них для всей совокупности являются различными случайными величинами. Вследствие этого при увеличении числа используемых методов (приборов) систематические погрешности взаимно компенсируются.

 

Одним из наиболее простых способов обнаружения и устране­ния переменных систематических погрешностей является графиче­ский метод, который заключается в построении графика последова­тельности неисправленных значений результатов единичных измерений. Расположение полученных точек позволяет обнаружить наличие закономерного изменения результатов измерений и сделать вывод о присутствии в них систематической погрешности.

На рисунке представлено несколько однократных измере­ний постоянной величины х₀, выполненных через равные проме­жутки времени. Если закон изменения систематической погрешности близок к линейному, то графический метод обеспечивает практиче­ски полное ее исключение.

 

Линейное изменение систематической погрешности

Исключение промахов

Если заранее известно, что какой-либо результат измерения получен из-за грубой ошибки при проведении измерений (невер­ный отсчет или запись показаний, сбой показаний прибора и т.п.), этот результат считается промахом и его следует исключить из рас­сматриваемой совокупности результатов измерений, не подвергая никаким проверкам.

Если же имеется сомнение, то каждый из про­махов подлежит статистической проверке. Существует несколько критериев для оценки промахов.

Если число измерений n ≥ 20 и распределение результатов измерений подчиняется нормальному закону, используют критерий «тpex сигм». По этому критерию считается, что результат х_i возник­ший с вероятностью

Р 0,003 (0,3%), маловероятен и его логично считать промахом при

 

 

При числе измерений n < 20 целесообразно применять крите­рий Романовского. При этом вычисляют отношение

 

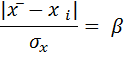
где x_i - результат, вызывающий сомнение; – среднее значение.

β_т – коэффициент, предельное значение которого определяют по таблице.

 

Уровень значимости q	Число измерений
n=4	n=6	n=8	n=10	n=12	n=14	n=16
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,05	1,71	2,10	2,27	2,41	2,52	2,69	2,78
0,10	1,69	2,00	2,17	2,29	2,39	2,49	2,62

При β ˃ β_т результат измерения х_i исключают («отбрасывают» ), так как этот результат является промахом.

Уровень значимостиq – это вероятность ошибочного отклонения (отвержения) гипотезы, в то время как она на самом деле верна. 0,01 вероятность того, что гипотеза неверна при β ˃ β_т и результат отброшен неверно.

Если число измерений невелико (n ≤10), то можно использовать критерий Шовэне. В этом случае считают, что результат x_i является промахом, если превышает значения, приведенные далее:

 

 

 

 

Пример. При измерении диаметра вала микрометром были получены значения. Определить, имеется ли среди результатов промах.

 

Измерение микрометром размера вала мм
№
И	14,24	14,26	14,28	14,28	14,31	14,34	14,40	14,41	14,42	14,42	14,45	14,80
№
И	14,34	14,40	14,41	14,42	14,42	14,28	14,28	14,31	14,34	14,26	14,28	14,31

 

Так как n > 20, для определения промахов используем критерий «трёх сигм».

 

 

 

 

 

 

 

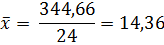
Сравнивая разницу с уровнем 3σ получим:

 

3σ = 0,33; 0,12 <0,33

 

следовательно, х₁ не является промахом.

Проведя анализ и других измерений, приходим к выводу, что промахом является измерение номер 12:

Пример. При измерении диаметра вала микрометром были полу­чены значения:

Измерение микрометром размера вала мм
№
И	12,24	12,26	12,28	12,28	12,31	12,34	12,40	12,41	12,42	12,42	12,45	12,80

Число измерений n=12. Определить, являет­ся ли последний результат x₁₂= 12,80 мм промахом при Р= 0,95 ( q= 1 - Р= 0,05).

Так как n < 20, для определения промахов используем критерий Романовского.

 

 

Для n = 12 и q = 0,05 β _т = 2,52(см. табл. …), т.е, β ≥ β_т и ре­зультат х_i = x₁₂ = 12,80 мм необходимо отбросить, так как он является промахом.

Пример. При измерении диаметра вала микрометром были полу­чены значения:

Измерение микрометром размера вала мм
№
И	30,12	30,27	30,28	30,29	30,32	30,38

Число изме­рений. Определить, является ли первый результат x₁=30,12 мм промахом. n = 6

Так как n < 10, для определения промахов используем критерий Шовине.

 

что больше, чем 1,7 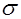= 0,1462 мм. Следовательно, причиной появления результата x_i=x₁=30,12 мм является промах и этот результат необходимо исключить из полученного ряда результатов измерений.

 

 

Дискретные и непрерывные случайные величины.

По своей физической природе случайные величины могут быть детерминированными и случайными.

Дискретной называют случайную величину, отдельные значения которой можно перенумеровать (число изделий, количество деталей – бракованных и годных и т.п.).

Непрерывной называют случайную величину, возможные значения которой заполняют некоторый промежуток (отклонение размера изготовленной детали от номинала, погрешность измерения, величина отклонения формы детали, высота микронеровностей и т.п.).

Случайная величина не может характеризоваться каким-то одним значением. Для неё необходимо указать множество возможных значений и вероятностные характеристики, заданные на этом множестве.

 

В том случае, если случайное событие выражается в виде числа, можно говорить о случайной величине. Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Выпадение некоторого значения случайной величины Х это случайное событие: Х = х_i. Среди случайных величин выделяют дискретные и непрерывные случайные величины.

Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.

Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.

Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют. Пусть задано некоторое х – действительное число и получена случайная величина X, при этом x > X. Требуется определить вероятность того, что случайная величина Х будет меньше этого фиксированного значения х.

Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что случайная величина Х в результате испытания примет значение меньшее значения х, то есть:

F (х) = Р(Х < х).

где х – произвольное действительное число.

Случайная величина (непрерывная или дискретная) имеет численные характеристики:

Математическое ожидание М (Х). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х.

Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания.

Среднее квадратическое отклонение σ(Х) для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии:

 

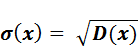
Случайная величина характеризуется в теории вероятностей законом ее распределения. Этот закон устанавливает связь между возможными значениями случайной величины и соответствующими этим значениям вероятностям их появления. Существует две формы описания закона распределения случайной величины - дифференциальная и интегральная. Причем, в метрологии в основном используется дифференциальная форма - закон распределения плотности вероятностей случайной величины.

Дифференциальный закон распределения характеризуется плотностью распределения вероятностей f(x) случайной величины х. Вероятность Р попадания случайной величины в интервал от х₁ до х₂ при этом дается формулой:

Графически эта вероятность представляет собой отношение площади под кривой f(x) в интервале от х₁ до х₂ к общей площади, ограниченной всей кривой распределения. Как правило, площадь под всей кривой распределения вероятностей нормируют на единицу.

В данном случае представлено распределение непрерывной случайной величины. Кроме них существуют и дискретные случайные величины, принимающие ряд определенных значений, которые можно пронумеровать.

Интегральный закон распределения случайной величины представляет собой функцию F(x), определяемую формулой

Вероятность, что случайная величина будет меньше х₁ дается значением функции F(х) при х = х₁:

Хотя закон распределения случайных величин является их полной вероятностной характеристикой, нахождение этого закона является довольно трудной задачей и требует проведения многочисленных измерений. Поэтому на практике для описания свойств случайной величины используют различные числовые характеристики распределений. К ним относятся моменты слу-чайных величин: начальные и центральные, которые представляют собой некоторые средние значения. При этом если усредняются величины, отсчитываемые от начала координат, то моменты называются начальными, а если от центра распределения – то центральными.

Начальный момент k-го порядка определяется формулой:

Наибольший практический интерес представляет начальный момент первого порядка - математическое ожидание случайной величины m₁ (k=1):

Математическое ожидание определяет положение центра группирования случайной величины, вокруг которого наблюдается ее рассеяние. Экспериментальной оценкой математического ожидания при многократных измерениях является среднее арифметическое значение измеряемой величины.

Центральный момент k-го порядка определяется формулой:

Особую роль играет центральный момент второго порядка. Он называется дисперсией D случайной величины и характеризует рассеяние отдельных значений этой величины:

На практике чаще используется среднее квадратическое отклонение σ (СКО) случайной величины, определяемое формулой:

 

Дрейф нуля в усилителях постоянного тока (УПТ). Самопроизвольное изменение напряжения на выходе при отсутствии напряжения на входе – входного сигнала.