Тема «Интегрирование простейших функций (вычисление определенных и неопределенных интегралов), вычисление площадей плоских фигур, решение прикладных задач».
Цели: научиться: вычислять неопределенные и определенные интегралы, площади плоских фигур; решать прикладные задачи.
Краткие теоретические сведения.
Определение. Дифференцируемая функция 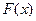 , определенная на некотором промежутке Х, называется
, определенная на некотором промежутке Х, называется 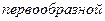 для функции
для функции 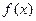 , определенной на этом же промежутке, если для всех Х из этого промежутка
, определенной на этом же промежутке, если для всех Х из этого промежутка 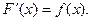
Теорема. Если функция 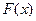 есть первообразная для функции
есть первообразная для функции 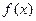 на некотором промежутке
на некотором промежутке 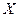 , то функция
, то функция 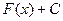 , где
, где 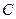 - произвольная постоянная, также является первообразной для функции
- произвольная постоянная, также является первообразной для функции 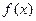 на этом же промежутке.
на этом же промежутке.
Определение. Совокупность всех первообразных для функции 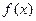 , определенных на некотором промежутке
, определенных на некотором промежутке 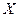 , называется неопределенным интегралом от функции
, называется неопределенным интегралом от функции 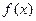 на этом промежутке и обозначается символом
на этом промежутке и обозначается символом 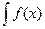
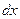 (читается: интеграл эф от икс де икс).
(читается: интеграл эф от икс де икс).
Если 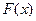 является первообразной для функции
является первообразной для функции 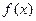 на промежутке
на промежутке 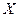 , то
, то 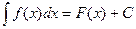 .
.
Функция 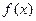 называется подынтегральной функцией,
называется подынтегральной функцией, 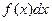 - подынтегральным выражением,
- подынтегральным выражением, 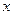 - переменной интегрирования, символ
- переменной интегрирования, символ 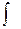 - знаком неопределенного интеграла,
- знаком неопределенного интеграла, 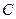 - постоянной интегрирования.
- постоянной интегрирования.
Основные свойства неопределенного интеграла.
1) Производная неопределенного интеграла равна подынтегральной функции.
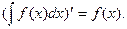
2) Дифференциал неопределенного интеграла равен подынтегральному выражению.
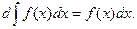
3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная.
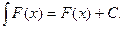
4) Постоянный множитель можно выносить за знак интеграла.
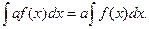

5) Интеграл от суммы непрерывных функций равен сумме интегралов слагаемых.
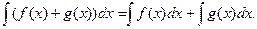
Таблица основных интегралов.
1. 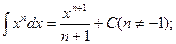 при
при 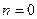
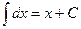 .
.
2. 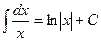 . 3.
. 3. 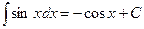 . 4.
. 4. 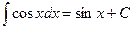 .
.
5. 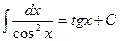 . 6.
. 6. 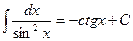 . 7.
. 7. 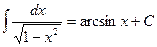 .
.
8. 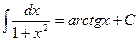 . 9.
. 9. 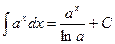 . 10.
. 10. 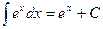 .
.
11. 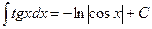 . 12.
. 12. 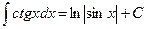 . 13.
. 13. 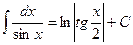 .
.
14. 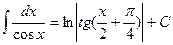 . 15.
. 15. 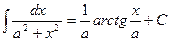 . 16.
. 16. 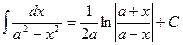 .
.
17. 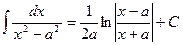 .18.
.18. 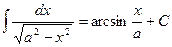 . 19.
. 19. 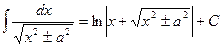 20.
20. 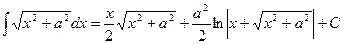 .
.
21. 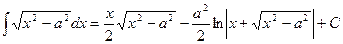 .
.
При вычислении интегралов, кроме формул интегрирования и основных свойств неопределенного интеграла, полезно применять следующее правило.
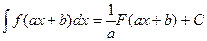 .
.
Методы интегрирования.
1) Непосредственное интегрирование.
Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
Пример 1.Найти 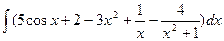 .
.
Используем свойства 5) и 4):
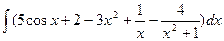 =
= 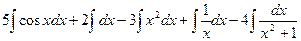 .
.
Далее, используя соответственно формулы 4), 1), 2), 8) таблицы основных интегралов, находим:
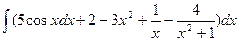
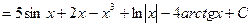 .
.
Пример 2. Вычислить интеграл 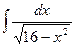 .
.
Интеграл табличный. Поэтому можно переходить к непосредственному интегрированию. По формуле 18), где 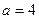 , получим
, получим
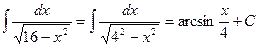 .
.
Пример 3. Вычислить интеграл 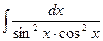 .
.
Интеграл не табличный, поэтому преобразуем его. Так как 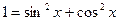 , то интеграл можно записать в виде
, то интеграл можно записать в виде
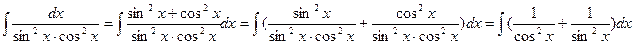 .
.
Применим свойство 5), имеем
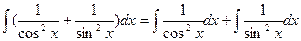 .
.
Получили два табличных интеграла. По формулам 5) и 6) находим
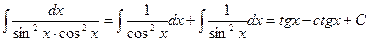 .
.
Пример 4. Вычислить интеграл 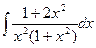 .
.
Так как 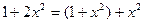 , то
, то
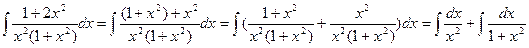 .
.
По формулам 1) и 8) получим
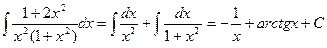 .
.
Пример 5. Вычислить интеграл 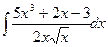 .
.
Предварительно числитель подынтегральной функции разделим на знаменатель, затем последовательно применим свойства 4), 5) и формулу 1), получим
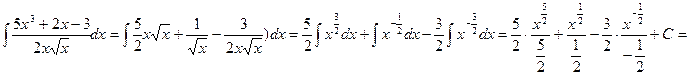
= 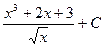 .
.
Пример 6. Вычислить интеграл 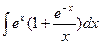 .
.
Раскроем скобки и применим табличные интегралы 2) и 10).
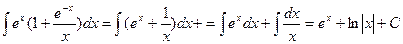 .
.
Метод подстановки.
Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла, т. е. прейти к непосредственному интегрированию. Такой метод называется методом подстановки или методом замены переменной, который основан на применении формулы 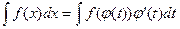 .
.
Пример 7. Вычислить интеграл 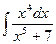 .
.
Положим 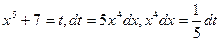 . Теперь переходим под знаком интеграла к новой переменной, берем получившийся интеграл и, наконец, возвращаемся к старой переменной. Получим
. Теперь переходим под знаком интеграла к новой переменной, берем получившийся интеграл и, наконец, возвращаемся к старой переменной. Получим 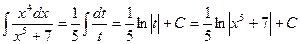 .
.
Пример 8. Вычислить интеграл 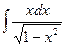 .
.
Положим 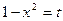 ; тогда
; тогда 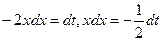 . Следовательно
. Следовательно
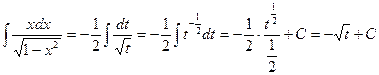 . Заменим
. Заменим 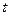 его выражением из подстановки, получим
его выражением из подстановки, получим 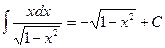 .
.
Пример 9. Вычислить интеграл 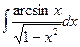 .
.
Положим 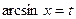 ; тогда
; тогда 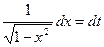 . Следовательно
. Следовательно 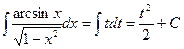 . Перейдя к переменной
. Перейдя к переменной 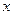 , окончательно получим
, окончательно получим 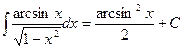 .
.
Пример 10. Вычислить интеграл 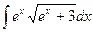 .
.
Положим 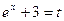 ; тогда
; тогда 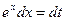 , Следовательно
, Следовательно 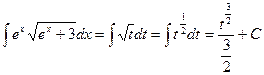 =
=
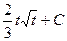 . Перейдя к переменной
. Перейдя к переменной 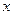 , окончательно получим
, окончательно получим 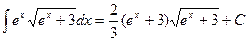 .
.
Пример 11. Вычислить интеграл 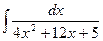 .
.
Из квадратного трехчлена выделим полный квадрат суммы:
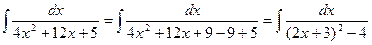 .
.
Положим 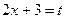 ; тогда
; тогда 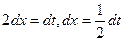 , Следовательно,
, Следовательно,
 .
.
Пример 12. Вычислить интеграл 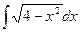 .
.
Так как 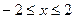 , то, положив
, то, положив 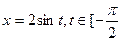 ;
; 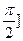 , найдем
, найдем 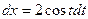 . Следовательно,
. Следовательно,

Перейдем в полученном результате снова к переменной 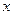 . Имеем
. Имеем 
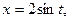
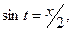
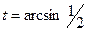 . Так как
. Так как 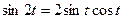 , а
, а 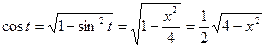 , то
, то 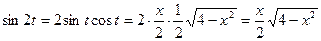 . Таким образом
. Таким образом
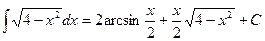 .
.
Интегрирование по частям.
Формулой интегрирования по частям в неопределенном интеграле называется формула
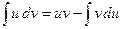 ,
,
Где 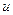 и
и 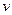 - дифференцируемые функции от
- дифференцируемые функции от 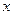 .
.
Пример 13. Вычислить интеграл 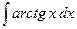 .
.
Положим  ,
, 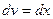 . Тогда
. Тогда 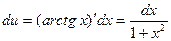 ;
; 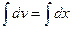 ,
, 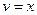 . Тогда по формуле имеем
. Тогда по формуле имеем 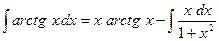 . В интеграле
. В интеграле 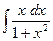 положим
положим 
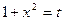
тогда 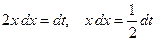 . Значит
. Значит 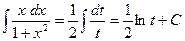 . Перейдем к переменной
. Перейдем к переменной 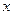 .
. 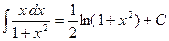 . Окончательно имеем
. Окончательно имеем 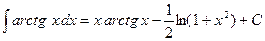 .
.
Пример 14. Вычислить интеграл 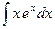 .
.
Положим 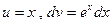 , найдем
, найдем 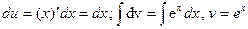 .
.
По формуле получим 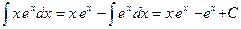 .
.
Пример 15. Вычислить интеграл 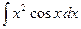 .
.
Положим 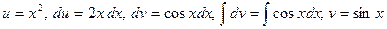 . Тогда по формуле имеем
. Тогда по формуле имеем
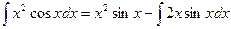 . В последнем интеграле положим
. В последнем интеграле положим 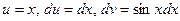 ,
,
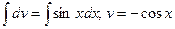 . Имеем
. Имеем 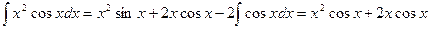 -
-
-2 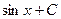 . Таким образом
. Таким образом 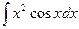 вычислен двукратным интегрированием по частям.
вычислен двукратным интегрированием по частям.
Определение. Приращение 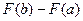 любой из первообразных функций
любой из первообразных функций 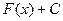 при изменении аргумента от
при изменении аргумента от 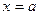 до
до 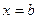 называется определенным интегралом от
называется определенным интегралом от 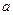 до
до 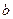 и обозначается
и обозначается 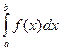 (читается: «интеграл от
(читается: «интеграл от 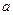 до
до 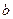 эф от икс де икс»). Числа
эф от икс де икс»). Числа 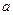 и
и 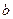 называются пределами интегрирования,
называются пределами интегрирования, 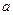 - нижним,
- нижним, 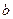 - верхним. Отрезок
- верхним. Отрезок 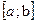 называется пределом интегрирования. Функция
называется пределом интегрирования. Функция 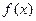 называется подынтегральной функцией, а переменная
называется подынтегральной функцией, а переменная 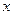 - переменной интегрирования.
- переменной интегрирования.
Таким образом, по определению 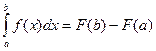 .
.
Это равенство называется формулой Ньютона-Лейбница.
Если интегрируемая на отрезке 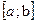 функция
функция 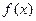 неотрицательна, то определенный интеграл
неотрицательна, то определенный интеграл 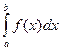 численно равен площади
численно равен площади 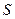 криволинейной трапеции, ограниченной графиком функции
криволинейной трапеции, ограниченной графиком функции 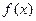 , осью абсцисс и прямыми
, осью абсцисс и прямыми 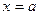 и
и 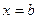 , т.е.
, т.е. 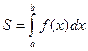 . (1)
. (1)
Основные свойства определенного интеграла.
1. По определению 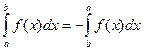
2. Постоянный множитель можно выносить за знак определенного интеграла, т.е.
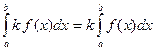 .
.
3. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов т.е.
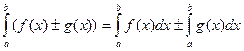 .
.
4. Каковы бы ни были числа 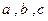 имеет место равенство
имеет место равенство
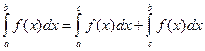 . 5. Если функция
. 5. Если функция 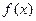 неотрицательна на отрезке
неотрицательна на отрезке 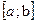 , где
, где 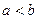 , то
, то 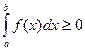
Чтобы вычислить определенный интеграл 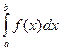 , нужно:
, нужно:
1) Найти соответствующий неопределенный интеграл 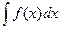 ;
;
2) В полученном выражении подставить вместо 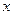 сначала верхний предел
сначала верхний предел 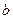 , а затем нижний предел
, а затем нижний предел 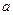 , и из результата первой подстановки вычесть результат второй.
, и из результата первой подстановки вычесть результат второй.
Коротко это правило записывается в виде формулы так:
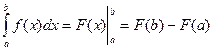 .
.
Пример 15. Вычислить 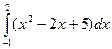 .
.
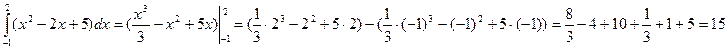 Методы вычисления определенного интеграла.
Методы вычисления определенного интеграла.
1. Вычисление определенного интеграла методом подстановки.
При вычислении определенного интеграла методом подстановки определенный интеграл 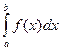 преобразуется с помощью подстановки
преобразуется с помощью подстановки 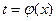 в определенный интеграл относительно новой переменной
в определенный интеграл относительно новой переменной 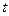 . При этом старые пределы интегрирования
. При этом старые пределы интегрирования 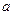 и
и 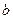 заменяются соответственно новыми пределами интегрирования
заменяются соответственно новыми пределами интегрирования 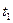 и
и 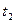 , которые находятся из исходной подстановки.
, которые находятся из исходной подстановки.
Пример 16. Вычислить 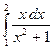 .
.
Положим 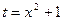 , тогда
, тогда 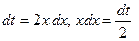 . Найдем новые пределы интегрирования. Подставляя в соотношение
. Найдем новые пределы интегрирования. Подставляя в соотношение 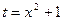 значения
значения 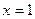 и
и  , соответственно получим
, соответственно получим 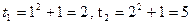 . Следовательно,
. Следовательно,
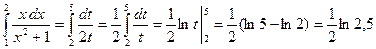 .
.
2. Интегрирование по частям в определенном интеграле.
Если функции 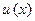 и
и 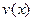 и их производные
и их производные 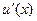 и
и 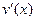 непрерывны в промежутке
непрерывны в промежутке 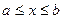 , то формула интегрирования по частям для определенного интеграла имеет вид
, то формула интегрирования по частям для определенного интеграла имеет вид
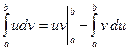 .
.
Пример 17. Вычислить 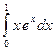 .
.
Положим 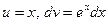 , тогда
, тогда 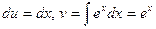 . Следовательно,
. Следовательно,
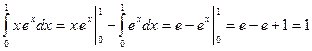 .
.
Вычисление площадей плоских фигур.
Площадь плоских фигур вычисляется по формуле (1).
Пример 18. Вычислить площадь фигуры, ограниченной
линиями 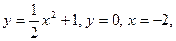
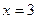 .
.
Сделаем чертеж. Фигура, площадь которой нужно
определить, есть криволинейная трапеция, ограниченная
сверху кривой 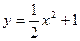 , снизу осью
, снизу осью 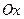 , а слева и справа
, а слева и справа
прямыми 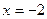 и
и 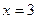 , Поэтому для решения задачи применим формулу (1).
, Поэтому для решения задачи применим формулу (1).
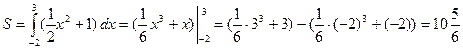 .
.
Если фигура ограничена графиками двух непрерывных на отрезке 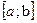 функций
функций 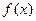 и
и 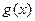 и прямыми
и прямыми 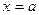 и
и 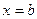 , где
, где 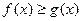 и
и 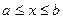 , то искомая площадь
, то искомая площадь 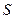 вычисляется по формуле
вычисляется по формуле 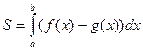 . (2)
. (2)
Пример 19. Вычислить площадь фигуры, ограниченной линиями 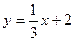 и
и 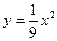 .
.
Сделаем чертеж. Пределы интегрирования
найдем из уравнения 
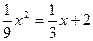 , т.е.
, т.е.
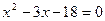 , откуда
, откуда 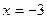 или
или 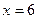 . Следовательно,
. Следовательно,
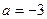 и
и 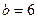 . Так как на отрезке
. Так как на отрезке 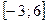 для
для
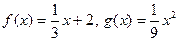 имеем
имеем 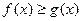 , то по
, то по
формуле (2) находим
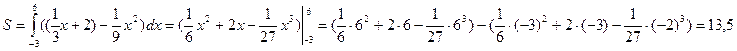 Применение определенного интеграла для решения физических и технических задач.
Применение определенного интеграла для решения физических и технических задач.
1) Вычисление пути, пройденного точкой.
Путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью 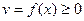 за промежуток времени от
за промежуток времени от 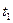 до
до 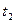 , вычисляется по формуле
, вычисляется по формуле 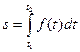 . (3)
. (3)
Пример 20. Скорость движения точки изменяется по закону 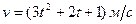 . Найти путь, пройденный точкой за 10с от начала движения.
. Найти путь, пройденный точкой за 10с от начала движения.
Согласно условию, 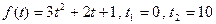 . По формуле (3) находим
. По формуле (3) находим
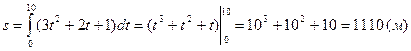 .
.
2) Вычисление работы силы.
Работа, произведенная переменной силой 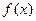 при перемещении по оси
при перемещении по оси 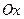 материальной точки от
материальной точки от  до
до 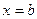 , находится по формуле
, находится по формуле 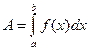 . (4)
. (4)
Пример 21. Вычислить работу силы 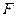 при сжатии пружины на 0,04м, если для сжатия ее на 0,01м нужна сила 10Н.
при сжатии пружины на 0,04м, если для сжатия ее на 0,01м нужна сила 10Н.
Для решения задачи на нахождение работы силы воспользуемся законом Гука: 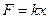 , Так как
, Так как 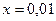 м при
м при 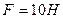 , то, подставляя эти значения в закон Гука получим
, то, подставляя эти значения в закон Гука получим 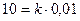 , откуда
, откуда 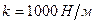 . Подставляя в это же равенство значение
. Подставляя в это же равенство значение 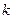 находим
находим 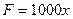 , т.е.
, т.е. 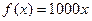 .
.
Искомую работу найдем по формуле (4), полагая 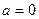 ,
, 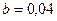 :
:
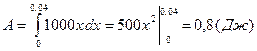
3) Вычисление силы давления жидкости.
Значение силы 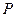 давления жидкости на горизонтальную площадку зависит от глубины погружения
давления жидкости на горизонтальную площадку зависит от глубины погружения 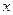 этой площадки. Сила давления на горизонтальную площадку вычисляется по формуле
этой площадки. Сила давления на горизонтальную площадку вычисляется по формуле 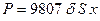 , где
, где 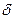 - плотность жидкости,
- плотность жидкости, 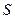 - площадь площадки,
- площадь площадки, 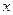 - глубина погружения площадки. Если площадка, испытывающая давление, не горизонтальна, то давление на нее различно на разных глубинах, следовательно, сила давления на площадку есть функция глубины ее погружения
- глубина погружения площадки. Если площадка, испытывающая давление, не горизонтальна, то давление на нее различно на разных глубинах, следовательно, сила давления на площадку есть функция глубины ее погружения 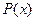 .
.
Пример 22. Вычислить силу давления на вертикальный прямоугольный шлюз с основанием 20 м и высотой 5 м (уровень воды совпадает с верхним обрезом шлюза).
На глубине 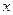 выделим горизонтальную полоску шириной
выделим горизонтальную полоску шириной 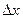 . Сила давления
. Сила давления 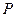 на стенку шлюза есть функция от
на стенку шлюза есть функция от 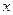 . Изменение глубины
. Изменение глубины 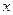 на малую величину
на малую величину  вызывает изменение силы давления
вызывает изменение силы давления 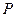 на малую величину
на малую величину 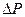 . Продифференцировав переменную
. Продифференцировав переменную 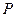 , получим приближенное значение
, получим приближенное значение 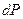 приращения
приращения 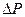 . Находим приближенное значение силы давления воды на эту полоску
. Находим приближенное значение силы давления воды на эту полоску 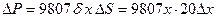 . Но
. Но 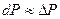 . Интегрируя
. Интегрируя 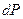 при изменении от 0 до 5, получим
при изменении от 0 до 5, получим 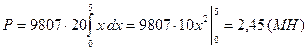 .
.
Задания для самостоятельной работы.
1. Найти интегралы.
1.1 а) 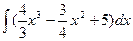 ; б)
; б) 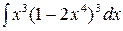 ; в)
; в) 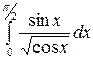 .
.
1.2 а) 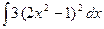 ; б)
; б) 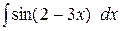 ; в)
; в) 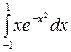 .
.
1.3 а) 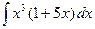 ; б)
; б) 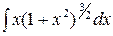 ; в)
; в) 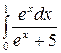 .
.
1.4 а) 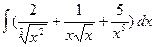 ; б)
; б) 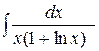 ; в)
; в) 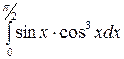 .
.
1.5 а) 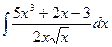 ; б)
; б) 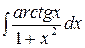 ; б)
; б) 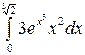 .
.
1.6 а) 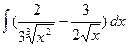 ; б)
; б) 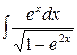 ; в)
; в) 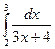 .
.
1.7 а) 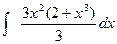 ; б)
; б) 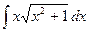 ; в)
; в) 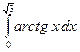 .
.
1.8 а) 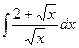 ; б)
; б) 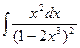 ; в)
; в) 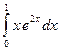 .
.
1.9 а) 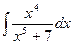 ; б)
; б) 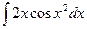 ; в)
; в) 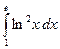 .
.
1.10 а) 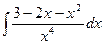 ; б)
; б) 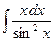 ; в)
; в) 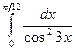 .
.
1.11 а) 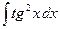 ; б)
; б) 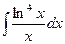 ; в)
; в) 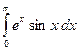 .
.
1.12 а) 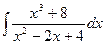 ; б)
; б) 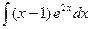 ; в)
; в) 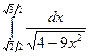 .
.
1.13 а) 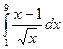 ; б)
; б) 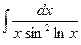 ; в)
; в) 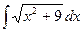 .
.
1.14 а) 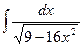 ; б)
; б) 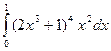 ; в)
; в) 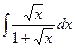 .
.
1.15 а) 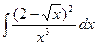 ; б)
; б) 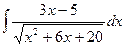 ; в)
; в) 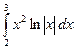 ;
;
1.16 а) 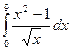 ; б)
; б) 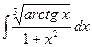 ; в)
; в) 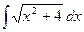 .
.
1.17 а) 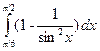 ; б)
; б) 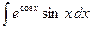 ; в)
; в) 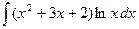 .
.
1.18 а) 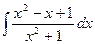 ; б)
; б) 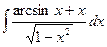 ; в)
; в) 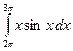 .
.
1.19 а) 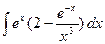 ; б)
; б) 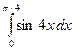 ; в)
; в) 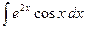 .
.
1.20 а) 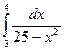 ; б)
; б) 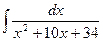 ; в)
; в) 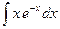 .
.
1.21 а) 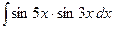 ; б)
; б) 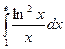 ; в)
; в) 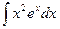 .
.
1.22 а) 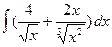 ; б)
; б) 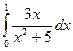 ; в)
; в) 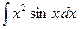 .
.
1.23 а) 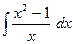 ; б)
; б) 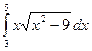 ; в)
; в) 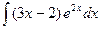 .
.
1.24 а) 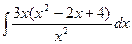 ; б)
; б) 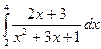 ; в)
; в) 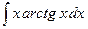 .
.
1.25 а) 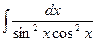 ; б)
; б) 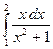 ; в)
; в) 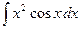 .
.
1.26 а) 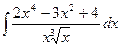 ; б)
; б) 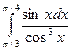 ; в)
; в) 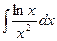 .
.
1.27 а)  ; б)
; б) 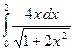 ; в)
; в) 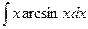 .
.
1.28 а) 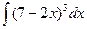 ; б)
; б) 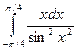 ; в)
; в) 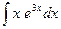 .
.
1.29 а) 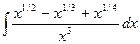 ; б)
; б) 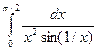 ; в)
; в) 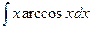 .
.
1.30 а) 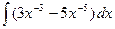 ; б)
; б)  ; в)
; в) 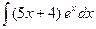 .
.
2. Вычислить площади фигур ограниченных линиями.
2.1 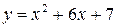 ,
, 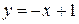 ; 2.2
; 2.2 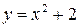 ,
,  ;
;
2.3 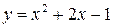 ,
, 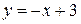 ; 2.4
; 2.4 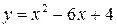 ,
, 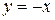 ;
;
2.5 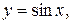
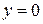 ,
, 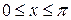 ; 2.6
; 2.6 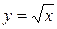 ,
, 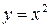 .
.
2.7 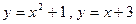 ; 2.8
; 2.8 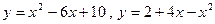 ; 2.9
; 2.9 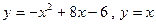 .
.
2.10 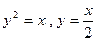 ; 2.11
; 2.11 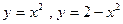 ; 2.12
; 2.12 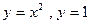 ; 2.13
; 2.13 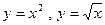 ;
;
2.14 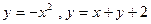 ; 2.15
; 2.15 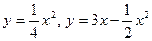 ; 2.16
; 2.16 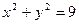 ; 2.17
; 2.17 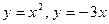 ;
;
2.18 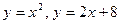 ; 2.19
; 2.19 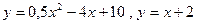 ; 2.20
; 2.20 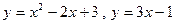 ;
;
2.21  ; 2.22
; 2.22 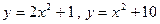 ; 2.23
; 2.23 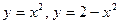 ;
;
2.24 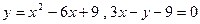 ; 2.25
; 2.25 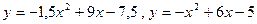 ;
;
2.26 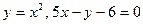 ; 2.27
; 2.27 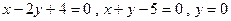 ; 2.28
; 2.28 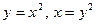 ;
;
2.29  ; 2.30
; 2.30 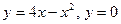 .
.
3. Решите задачи.
3.1 Вычислите работу совершенную при сжатии пружины на 0, 04м, если для сжатия ее на 0, 01м нужна сила 20Н.
3.2 Скорость точки, движущейся прямолинейно, задана уравнением 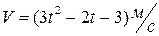 . Вычислить путь, пройденный точкой за четвертую секунду и путь, пройденный точкой до остановки.
. Вычислить путь, пройденный точкой за четвертую секунду и путь, пройденный точкой до остановки.
3.3 Вычислить силу давления на вертикальную прямоугольную пластину с основанием 2м и высотой 4м. Уровень воды совпадает с верхним основанием пластины.
3.4 Пружина растянута на 0,02м под действием силы 60Н. Какую работу производит эта сила, растягивая пружину на 0,12м?
3.5 Скорость движения точки 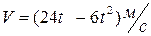 . Найдите: а) путь, пройденный точкой за третью секунду; б) путь, пройденный точкой до остановки.
. Найдите: а) путь, пройденный точкой за третью секунду; б) путь, пройденный точкой до остановки.
3.6Цилиндрический стакан наполнен маслом. Вычислите силу давления масла на боковую поверхность стакана, если высота его 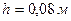 , радиус его основания
, радиус его основания 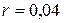 м, плотность масла
м, плотность масла 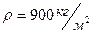 .
.
3.7 Найти силу давления масла на квадратную вертикально расположенную пластинку со стороной 0,3м, если верхний край пластинки горизонтален и лежит на 0,5м ниже поверхности масла (Плотность масла 900кг/ 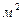 ).
).
3.8 Прямоугольная пластинка размерами 6 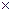 4
4 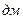 погружена в воду так, что большая ее сторона лежит на поверхности воды, а меньшая занимает вертикальное положение. Найти силу давления воды на пластинку.
погружена в воду так, что большая ее сторона лежит на поверхности воды, а меньшая занимает вертикальное положение. Найти силу давления воды на пластинку.
3.9 Найти путь 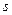 , пройденный телом за 10 с после начала движения, если скорость тела
, пройденный телом за 10 с после начала движения, если скорость тела  задается формулой
задается формулой 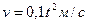 .
.
3.10 Какую работу нужно затратить, чтобы растянуть пружину на 4 см, если сила в 1 Н растягивает её на 2 см?
3.11 Материальная точка движется со скоростью, определяемой формулой 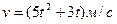 . Найти путь, пройденный этой точкой с момента
. Найти путь, пройденный этой точкой с момента 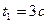 до момента
до момента 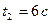 .
.
3.12 Вычислить путь, пройденный свободно падающим телом за 14 с, если известно, что скорость свободного падения определяется формулой 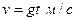 . Сопротивление воздуха не учитывается.
. Сопротивление воздуха не учитывается.
3.13 Вычислить работу, произведенную при сжатии пружины на 6 см, если для сжатия ее на 1см нужна сила в 1 Н.
3.14 Вычислить работу растяжения на 0,001 м медной проволоки длиной 1 м с радиусом сечения 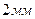 . Модуль упругости для меди 12 000
. Модуль упругости для меди 12 000 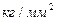 .
.
3.15 Скорость движения точки изменяется по закону 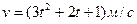 . Найти путь пройденный точкой за 10 с от начала движения.
. Найти путь пройденный точкой за 10 с от начала движения.
3.16 Пружина растягивается на 0,02 м под действием силы 100 Н. Какую производит эта сила, растягивая пружину на 0,12 м.
3.17 Вычислить силу давления воды на вертикальную прямоугольную стенку с основанием 2 м и высотой 6 м. Уровень воды совпадает с верхним обрезом стенки.
3.18 Под действием силы 80 Н пружина растягивается на 0,02 м. Первоначальная длина пружины равна 0,15 м. Какую работу надо совершить, чтобы растянуть ее до 0,2 м?
3.19 Скорость движения точки 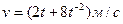 . Найдите ее путь за 2-ю секунду.
. Найдите ее путь за 2-ю секунду.
3.20 Скорость движения точки 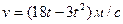 .Найдите путь, пройденный точкой от начала движения до ее полной остановки.
.Найдите путь, пройденный точкой от начала движения до ее полной остановки.
3.21 Скорость движения точки 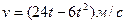 . Найдите путь пройденный точкой за 3 с от начала движения и за 3-ю секунду.
. Найдите путь пройденный точкой за 3 с от начала движения и за 3-ю секунду.
3.22 Для сжатия пружины на 0,03 м необходимо совершить работу 16 Дж. На какую длину можно сжать пружину, совершив работу в 144 Дж?
3.23 Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью 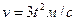 , второе – со скоростью
, второе – со скоростью 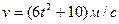 . На каком расстоянии друг от друга они окажутся через 10 с?
. На каком расстоянии друг от друга они окажутся через 10 с?
3.24 Тело брошено с земли вертикально вверх со скоростью