Постановка задачи. Ранее мы рассмотрели метод критических работ для совместного планирования и назначения, или масштабирования, процессов с целью выбора и оптимизации архитектурных решений вычислительных ресурсов. Напомним, понятие процесса охватывает операции, или задачи (атомарные действия), задания (цепочки двух и более операций) и работы (последовательности операций и заданий). Реализация этого метода предполагает масштабируемость ресурсов, состоящих из процессорных узлов и коммуникационной среды, или каналов обмена данными, и самой модели обработки данных. Это означает возможность использования дополнительных ресурсов, помимо базового набора процессоров и каналов обмена, а также допустимое, при определенных условиях, изменение априорных параметров процессов, полученных для базовых ресурсов.
Общая схема масштабирования, включает итеративное применение двух этапов. На первом из них осуществляется планирование и назначение критических работ. Планирование и назначение очередной критической работы может вызвать коллизию параллельных процессов, конкурирующих за использование одного и того же ресурса. Для этого на втором этапе при разрешении коллизии вводится дополнительный экземпляр ресурса. Требование разрешения коллизий выражается одним из условий допустимости масштаба 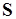 .
.
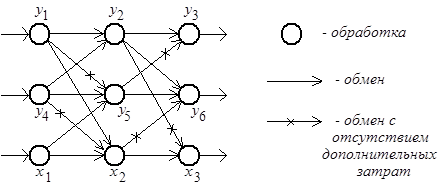
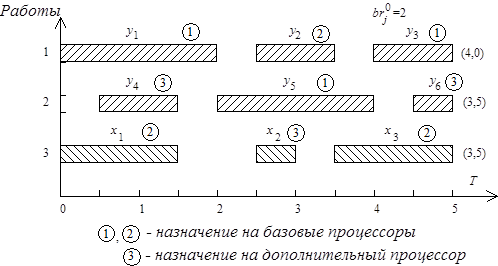
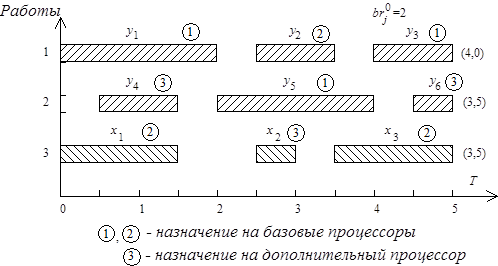
На рис. 6.12 приведен пример коллизии операций обработки. Граф на рис. 6.12, а иллюстрирует взаимосвязи между операциями обработки трех работ 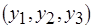 ,
, 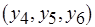 и
и 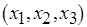 , конкурирующих за два доступных экземпляра процессора
, конкурирующих за два доступных экземпляра процессора 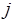 -го типа. Длительности выполнения операций графически представлены на рис. 6.12, б в некоторых единицах времени: например, длительность операции
-го типа. Длительности выполнения операций графически представлены на рис. 6.12, б в некоторых единицах времени: например, длительность операции 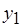 равна двум единицам, длительность операции
равна двум единицам, длительность операции 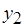 - одной единице и т.д. Операциям обмена данными на рис. 6.12, а соответствуют дуги. Дуги, обозначенные крестиками, представляют операции обмена, не требующие дополнительных затрат времени и ресурсов в случае, если соответствующие операции обработки, например
- одной единице и т.д. Операциям обмена данными на рис. 6.12, а соответствуют дуги. Дуги, обозначенные крестиками, представляют операции обмена, не требующие дополнительных затрат времени и ресурсов в случае, если соответствующие операции обработки, например 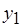 и
и  ,
, 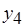 и
и 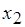 , назначаются на один и тот же процессор. Подробнее об этом будет сказано ниже в этом же параграфе. Значения длительности всех необходимых операций обмена приняты одинаковыми, равными 0,5 единицы времени. На рис. 6.12, б временные интервалы, которые могут быть использованы для обмена данными, представлены пробелами, например, между операциями
, назначаются на один и тот же процессор. Подробнее об этом будет сказано ниже в этом же параграфе. Значения длительности всех необходимых операций обмена приняты одинаковыми, равными 0,5 единицы времени. На рис. 6.12, б временные интервалы, которые могут быть использованы для обмена данными, представлены пробелами, например, между операциями 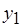 и
и 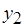 ,
, 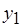 и
и 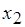 ,
, 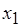 и
и 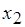 и т.п. В скобках на рис. 6.12, б указана суммарная длительность операций обработки: четыре единицы времени для работы
и т.п. В скобках на рис. 6.12, б указана суммарная длительность операций обработки: четыре единицы времени для работы 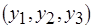 , 3,5 единицы для работ
, 3,5 единицы для работ 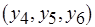 и
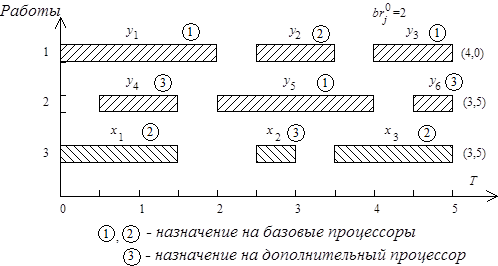
и 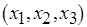 . Показанная на рис. 6.12, б коллизия вызвана планированием и назначением третьей работы
. Показанная на рис. 6.12, б коллизия вызвана планированием и назначением третьей работы 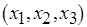 , первые две работы
, первые две работы 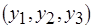 и
и 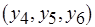 могут использовать два доступных базовых процессора. Для разрешения коллизии необходимо ввести дополнительный процессор того же типа.
могут использовать два доступных базовых процессора. Для разрешения коллизии необходимо ввести дополнительный процессор того же типа.
а)

б)
Рис. 6.12. Информационный граф (а) и коллизия процессов обработки (б)
Как уже подчеркивалось, после разрешения коллизий должен сохраняться промежуточный план операций обработки данных, хотя при этом и могут быть исключены затраты на обмен данными из-за того, что обработка выполняется на одном и том же процессоре. Это является необходимым условием сходимости алгоритмов масштабирования.
Разрешение коллизии заключается в таком изменении назначения 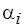 одной из попарно конкурирующих операций, при котором, по крайней мере, не уменьшается суммарное время использования процессоров и не увеличивается суммарная загрузка каналов обмена данными, задействованных до возникновения коллизии. Это требование может быть формализовано на основе введения такого критерия, как коэффициент использования
одной из попарно конкурирующих операций, при котором, по крайней мере, не уменьшается суммарное время использования процессоров и не увеличивается суммарная загрузка каналов обмена данными, задействованных до возникновения коллизии. Это требование может быть формализовано на основе введения такого критерия, как коэффициент использования 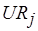 ресурсов
ресурсов 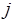 -го типа. При этом он может вводиться не только как вторичный показатель эффективности при разрешении коллизий, но и как основной критерий в формальной постановке задачи масштабирования. Для
-го типа. При этом он может вводиться не только как вторичный показатель эффективности при разрешении коллизий, но и как основной критерий в формальной постановке задачи масштабирования. Для 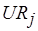 должно выполняться свойство аддитивной сепарабельности.
должно выполняться свойство аддитивной сепарабельности.
Обозначим через  коэффициент использования
коэффициент использования 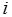 -й операцией в
-й операцией в 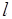 -м действии программы экземпляра
-м действии программы экземпляра 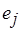 ресурса типа
ресурса типа 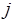 . Для процессоров он имеет следующий вид:
. Для процессоров он имеет следующий вид:
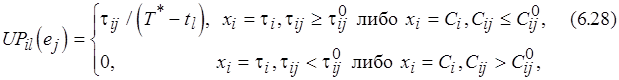
где 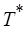 – крайний срок завершения программы;
– крайний срок завершения программы;  – суммарная длительность операций обмена в
– суммарная длительность операций обмена в 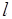 -м действии.
-м действии.
Для каналов обмена  выглядит так:
выглядит так:
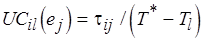 , (6.29)
, (6.29)
где 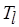 – суммарная длительность операций обработки в
– суммарная длительность операций обработки в 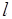 -м действии;
-м действии; 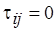 , если операции обработки, которым соответствует
, если операции обработки, которым соответствует 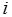 -я операция обмена, назначаются на один и тот же процессор;
-я операция обмена, назначаются на один и тот же процессор; 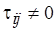 – в противном случае.
– в противном случае.
Коэффициент использования экземпляра 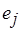 в
в 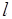 -м действии:
-м действии:
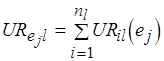 , (6.30)
, (6.30)
где 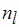 – число операций
– число операций 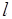 -го действия,
-го действия,  для операций обработки определяется по (6.28), а для операций обмена – по (6.29).
для операций обработки определяется по (6.28), а для операций обмена – по (6.29).
Через 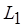 обозначим число действий программы, выполняемых независимо от условных ветвлений. Пусть
обозначим число действий программы, выполняемых независимо от условных ветвлений. Пусть 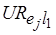 , где
, где  , вычисляется по (6.30). Положим,
, вычисляется по (6.30). Положим, 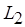 – число
– число 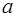 -компонентных наборов альтернативных действий с коэффициентами использования
-компонентных наборов альтернативных действий с коэффициентами использования 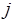 -го типа ресурсов на альтернативных путях, равными
-го типа ресурсов на альтернативных путях, равными 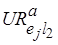 , где
, где 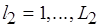 , и определяемыми по (6.30). Коэффициент использования экземпляра
, и определяемыми по (6.30). Коэффициент использования экземпляра 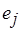 в программе равен
в программе равен
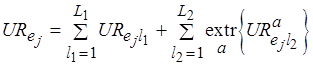 . (6.31)
. (6.31)
Для процессоров в (6.31) берется минимум коэффициента  , а для каналов обмена – максимум коэффициента
, а для каналов обмена – максимум коэффициента 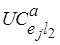 по всем альтернативным действиям программы.
по всем альтернативным действиям программы.
Наконец, коэффициент использования 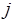 -го типа ресурсов:
-го типа ресурсов:
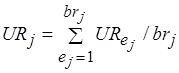 , (6.32)
, (6.32)
где  – общий уровень ресурса типа
– общий уровень ресурса типа  (например, число процессоров или каналов обмена типа
(например, число процессоров или каналов обмена типа  ), задействованный до возникновения коллизии, при этом
), задействованный до возникновения коллизии, при этом  вычисляется по (6.31).
вычисляется по (6.31).
Формальная постановка задачи оптимального разрешения коллизий операций обработки данных заключается в том, чтобы обеспечить максимум коэффициента 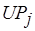 использования процессоров соответствующего типа согласно (6.32) и выполнить необходимое условие разрешения. В случае приближенного разрешения коллизий значение коэффициента
использования процессоров соответствующего типа согласно (6.32) и выполнить необходимое условие разрешения. В случае приближенного разрешения коллизий значение коэффициента 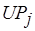 не должно уменьшаться.
не должно уменьшаться.
Коэффициенты 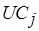 использования каналов обмена вводятся с учетом следующих особенностей операций обмена. Во-первых, в результате масштабирования не уменьшаются значения их длительности и стоимости использования каналов. Во-вторых, операции обмена данными исключаются, если последовательно выполняемые операции обработки данных назначаются на один и тот же процессор. Следовательно, при разрешении коллизий по обмену нужно учитывать историю их возникновения по всей системе работ и, если потребуется, выполнить повторное переназначение на каналы обмена.
использования каналов обмена вводятся с учетом следующих особенностей операций обмена. Во-первых, в результате масштабирования не уменьшаются значения их длительности и стоимости использования каналов. Во-вторых, операции обмена данными исключаются, если последовательно выполняемые операции обработки данных назначаются на один и тот же процессор. Следовательно, при разрешении коллизий по обмену нужно учитывать историю их возникновения по всей системе работ и, если потребуется, выполнить повторное переназначение на каналы обмена.
Формальная постановка задачи оптимального (приближенного) разрешения коллизий операций обмена данными состоит в том, чтобы обеспечить минимум (неувеличение) коэффициента 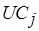 использования каналов обмена соответствующего типа согласно (6.32) с соблюдением условия разрешения.
использования каналов обмена соответствующего типа согласно (6.32) с соблюдением условия разрешения.
Условно оптимальное и приближенное разрешение коллизий. Коллизии процессов (см. рис. 6.12, б) могут быть представлены двудольным графом 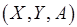 , множество
, множество  ребер которого отражает попарную конкуренцию за ресурс (рис. 6.13, а). При этом
ребер которого отражает попарную конкуренцию за ресурс (рис. 6.13, а). При этом 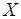 – множество операций работы, планирование и назначение которой вызывает коллизии, а
– множество операций работы, планирование и назначение которой вызывает коллизии, а 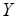 – множество операций ранее назначенных работ.
– множество операций ранее назначенных работ.
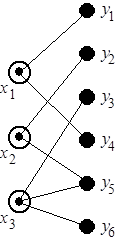
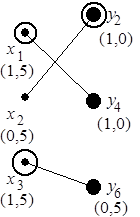

а) б) в)
Рис. 6.13. Двудольные графы "многослойной" коллизии (а), условно оптимального (б) и приближенного (в) ее разрешения
Коллизии в общем случае носят "многослойный" характер, т.е. охватывают процессы более чем двух работ (см. рис. 6.12, б и рис. 6.13, а). Это требует согласованного изменения соответствующих назначений на ресурсы. Так, взаимозависимыми являются назначения операций 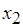 ,
, 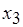 и
и 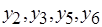 . Если пытаться разрешить коллизии, последовательно рассматривая попарно конкурирующие операции, то придется перебрать
. Если пытаться разрешить коллизии, последовательно рассматривая попарно конкурирующие операции, то придется перебрать 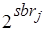 вариантов назначения, где
вариантов назначения, где 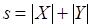 ,
, 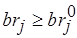 . Для рассматриваемого примера их число равно
. Для рассматриваемого примера их число равно 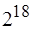 . Хотя при этом и возможно оптимальное разрешение коллизий, такой подход может оказаться неприемлемым с позиций алгоритмической реализации.
. Хотя при этом и возможно оптимальное разрешение коллизий, такой подход может оказаться неприемлемым с позиций алгоритмической реализации.
Выделим из множества 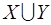 минимальное вершинное покрытие
минимальное вершинное покрытие 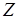 , так что все ребра множества
, так что все ребра множества  инцидентны вершинам из
инцидентны вершинам из  . На рис. 6.13, а
. На рис. 6.13, а 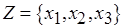 . Вершины подмножеств
. Вершины подмножеств 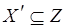 и
и 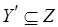 будем называть
будем называть 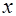 - и
- и 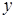 -вершинами покрытия. Обозначим через
-вершинами покрытия. Обозначим через 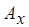 и
и 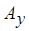 множества инцидентных им ребер, а через
множества инцидентных им ребер, а через 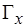 и
и  множества образов
множества образов 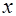 - и
- и 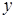 -вершины соответственно. Пусть имеются такие
-вершины соответственно. Пусть имеются такие 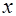 -вершины
-вершины 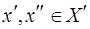 , что
, что 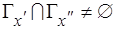 , а число их равно
, а число их равно 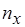 . Положим,
. Положим, 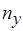 – число
– число 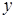 -вершин
-вершин 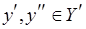 таких, что
таких, что 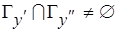 . Обозначим через
. Обозначим через 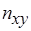 число общих ребер, инцидентных вершинам из
число общих ребер, инцидентных вершинам из 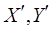 . Так, в рассматриваемом примере (см. рис. 6.13, а)
. Так, в рассматриваемом примере (см. рис. 6.13, а) 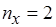 (
(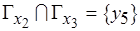 ),
), 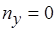 ,
, 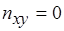 . Если
. Если 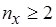 ,
, 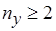 , то число допустимых вариантов оптимального разрешения коллизий на основе выделения минимального вершинного покрытия не больше чем
, то число допустимых вариантов оптимального разрешения коллизий на основе выделения минимального вершинного покрытия не больше чем 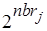 , где
, где 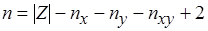 . Действительно, если
. Действительно, если  (
(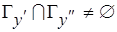 ), то назначения операций, которым сопоставлены вершины
), то назначения операций, которым сопоставлены вершины 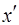 и
и 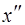 (
(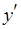 и
и 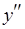 ), должны быть одинаковыми. Следовательно, число
), должны быть одинаковыми. Следовательно, число 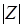 переназначаемых операций уменьшается на величину
переназначаемых операций уменьшается на величину 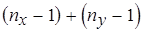 . Положим,
. Положим, 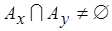 . Тогда назначения операций, представленных соответствующими
. Тогда назначения операций, представленных соответствующими 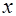 -,
-, 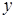 -вершинами, должны быть различными. Это приводит к дополнительному уменьшению
-вершинами, должны быть различными. Это приводит к дополнительному уменьшению 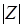 на число
на число 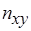 . Для примера на рис. 6.13, а из двух переназначаемых операций, которым соответствуют вершины
. Для примера на рис. 6.13, а из двух переназначаемых операций, которым соответствуют вершины  , можно выбрать любую, поскольку они должны иметь одинаковые назначения, отличные от назначения операции, которая представлена вершиной
, можно выбрать любую, поскольку они должны иметь одинаковые назначения, отличные от назначения операции, которая представлена вершиной 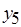 . Поскольку
. Поскольку  , то
, то 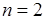 , и число вариантов переназначения операций сокращается до
, и число вариантов переназначения операций сокращается до  . Однако необходимо заметить, что при таком разрешении коллизий сначала нужно найти минимальное вершинное покрытие. При использовании метода Хопкрофта – Карпа эта задача может быть решена за время порядка
. Однако необходимо заметить, что при таком разрешении коллизий сначала нужно найти минимальное вершинное покрытие. При использовании метода Хопкрофта – Карпа эта задача может быть решена за время порядка 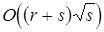 , где
, где 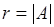 (см. Краткую сводку необходимых понятий). Далее нужно найти компоненты связности в графе
(см. Краткую сводку необходимых понятий). Далее нужно найти компоненты связности в графе  , чтобы выявить
, чтобы выявить 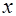 - и
- и 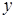 -вершины, пересечения образов которых не пусты, а также наличие общих ребер из
-вершины, пересечения образов которых не пусты, а также наличие общих ребер из 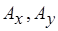 . Если применить метод поиска в глубину, то эта процедура потребует дополнительного времени порядка
. Если применить метод поиска в глубину, то эта процедура потребует дополнительного времени порядка 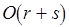 (см. Краткую сводку необходимых понятий). Таким образом, и этот подход может оказаться неприемлемым при большом числе
(см. Краткую сводку необходимых понятий). Таким образом, и этот подход может оказаться неприемлемым при большом числе 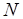 операций и возникновении "многослойных" коллизий. Разумеется, в вырожденном случае, когда попарные конкуренции независимы, т.е. в соответствующем двудольном графе нет двух ребер, инцидентных одной вершине, для разрешения коллизий достаточно последовательного просмотра
операций и возникновении "многослойных" коллизий. Разумеется, в вырожденном случае, когда попарные конкуренции независимы, т.е. в соответствующем двудольном графе нет двух ребер, инцидентных одной вершине, для разрешения коллизий достаточно последовательного просмотра 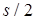 ребер и такого переназначения, которое, по крайней мере, не ухудшает значения коэффициента использования ресурса соответствующего типа. Тем не менее и при этом необходимо нахождение компонент связности в двудольном графе коллизий.
ребер и такого переназначения, которое, по крайней мере, не ухудшает значения коэффициента использования ресурса соответствующего типа. Тем не менее и при этом необходимо нахождение компонент связности в двудольном графе коллизий.
Рассмотрим, каким образом можно понизить сложность алгоритмов разрешения "многослойных" коллизий, учитывая свойство аддитивной сепарабельности критериев. Если требуется максимизировать (минимизировать) значение коэффициента использования процессоров (каналов обмена данными), то необходимо выбрать цепочку операций ранее назначенных работ с минимальной (максимальной) суммарной длительностью. Тогда двудольный граф  "многослойной" коллизии может быть заменен взвешенным двудольным графом
"многослойной" коллизии может быть заменен взвешенным двудольным графом 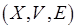 "двуслойной" коллизии, где
"двуслойной" коллизии, где 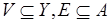 . Вес каждой вершины – длительность операции, причем сумма весов вершин в
. Вес каждой вершины – длительность операции, причем сумма весов вершин в 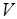 является наименьшей или наибольшей в зависимости от того, разрешаются коллизии процессов обработки или обмена данными.
является наименьшей или наибольшей в зависимости от того, разрешаются коллизии процессов обработки или обмена данными.
На рис. 6.13, б приведен пример графа 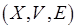 , в скобках рядом с вершинами указаны длительности соответствующих операций обработки (см. рис. 6.12, б),
, в скобках рядом с вершинами указаны длительности соответствующих операций обработки (см. рис. 6.12, б), 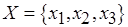 ,
, 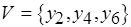 . Сопоставив рис. 6.12, б и рис. 6.13, а, б, нетрудно заметить, что последовательность
. Сопоставив рис. 6.12, б и рис. 6.13, а, б, нетрудно заметить, что последовательность 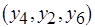 является системой различных представителей (трансверсалью) семейства
является системой различных представителей (трансверсалью) семейства 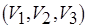 подмножеств множества
подмножеств множества 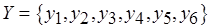 , а
, а 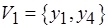 ,
, 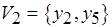 ,
, 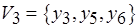 . Число подмножеств семейства совпадает с числом операций работы 3, вступающих в коллизии с операциями ранее назначенных работ 1, 2 (см. рис. 6.12, б).
. Число подмножеств семейства совпадает с числом операций работы 3, вступающих в коллизии с операциями ранее назначенных работ 1, 2 (см. рис. 6.12, б).
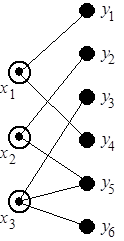
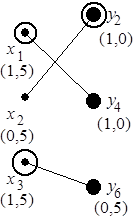

Таким образом, возможен следующий конструктивный подход к условно оптимальному разрешению "многослойной" коллизии путем сведения ее к "двуслойной". Пусть 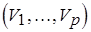 – семейство необязательно непересекающихся подмножеств множества
– семейство необязательно непересекающихся подмножеств множества 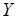 , представленное с помощью взвешенного двудольного графа
, представленное с помощью взвешенного двудольного графа 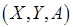 "многослойной" коллизии, причем
"многослойной" коллизии, причем 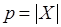 , а вес каждой вершины – длительность соответствующей операции. Необходимо найти трансверсаль для
, а вес каждой вершины – длительность соответствующей операции. Необходимо найти трансверсаль для 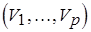 с наименьшим (наибольшим) весом и построить двудольный граф "двуслойной" коллизии
с наименьшим (наибольшим) весом и построить двудольный граф "двуслойной" коллизии 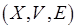 , где
, где 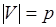 , а ребра из
, а ребра из 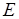 образуют паросочетание мощности
образуют паросочетание мощности 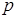 (см. рис. 6.13, б). Далее, последовательно просматривая смежные пары вершин (ребра) этого графа, требуется из пары выделить вершину с меньшим (большим) весом. На рис. 6.13, б это – вершины
(см. рис. 6.13, б). Далее, последовательно просматривая смежные пары вершин (ребра) этого графа, требуется из пары выделить вершину с меньшим (большим) весом. На рис. 6.13, б это – вершины 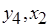 и
и 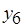 . Этим вершинам соответствуют операции, назначаемые на вновь вводимый экземпляр ресурса.
. Этим вершинам соответствуют операции, назначаемые на вновь вводимый экземпляр ресурса.
Такое разрешение коллизий является условно оптимальным, поскольку сведение "многослойной" коллизии к "двуслойной" не позволяет учесть всех 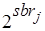 вариантов назначения.
вариантов назначения.
Сложность условно оптимального разрешения "многослойных" коллизий определяется трудоемкостью поиска трансверсали с наименьшим (наибольшим) весом. На основании теоремы Холла можно утверждать, что трансверсаль семейства 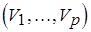 существует (см. Краткую сводку необходимых понятий). Действительно, пусть
существует (см. Краткую сводку необходимых понятий). Действительно, пусть 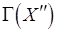 – множество вершин, смежных с вершинами из подмножества
– множество вершин, смежных с вершинами из подмножества 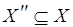 . Ясно, что
. Ясно, что 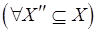
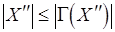 . В противном случае вообще не возникало бы коллизий. Рассмотрим следующую пару
. В противном случае вообще не возникало бы коллизий. Рассмотрим следующую пару 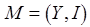 , где
, где 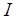 – семейство частичных трансверсалей семейства
– семейство частичных трансверсалей семейства 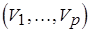 . В соответствии с теоремой Эдмондса и Фалкерсона пара
. В соответствии с теоремой Эдмондса и Фалкерсона пара 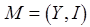 является матроидом (см. Краткую сводку необходимых понятий). Следовательно, может быть применен жадный алгоритм для матроида трансверсалей. Если для поиска чередующейся цепи (см. Краткую сводку необходимых понятий) использовать метод поиска в глубину, то общая сложность жадного алгоритма составит
является матроидом (см. Краткую сводку необходимых понятий). Следовательно, может быть применен жадный алгоритм для матроида трансверсалей. Если для поиска чередующейся цепи (см. Краткую сводку необходимых понятий) использовать метод поиска в глубину, то общая сложность жадного алгоритма составит 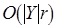 , где
, где 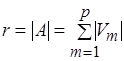 .
.
На рис. 6.13, б приведен пример графа "двуслойной" коллизии, где 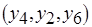 является трансверсалью, соответствующей операциям с наименьшей суммарной длительностью. Конкуренция в таком графе разрешается при последовательном просмотре ребер, а преимущество всегда отдается вершине с большим весом. Для рассматриваемого примера это – вершины
является трансверсалью, соответствующей операциям с наименьшей суммарной длительностью. Конкуренция в таком графе разрешается при последовательном просмотре ребер, а преимущество всегда отдается вершине с большим весом. Для рассматриваемого примера это – вершины 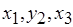 . Следовательно, соответствующие операции назначаются на базовые процессоры, а для операций
. Следовательно, соответствующие операции назначаются на базовые процессоры, а для операций 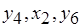 вводится дополнительный процессор. На рис. 6.12, б показана диаграмма работ после условно оптимального разрешения коллизий. Коэффициент использования процессоров
вводится дополнительный процессор. На рис. 6.12, б показана диаграмма работ после условно оптимального разрешения коллизий. Коэффициент использования процессоров 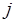 -го типа равен
-го типа равен 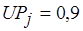 .
.
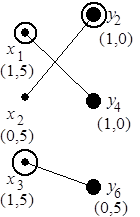
В случае приближенного разрешения коллизий по операциям обработки (обмена) не должно уменьшаться (увеличиваться) суммарное время использования процессоров (каналов обмена), введенных до возникновения коллизий. Тогда граф "многослойной" коллизии (см. рис. 6.13, а) может быть заменен двудольным графом "двуслойной" коллизии, в которой участвуют работа с наименьшей (наибольшей) суммарной длительностью операций обработки (обмена) и работа, масштабирование которой вызывает коллизии. На рис. 6.12, б это – работы 2 и 3. Попарные независимые конкуренции операций представлены различными компонентами связности (рис. 6.13, в).


Конкуренция между операциями обработки (обмена) разрешается в пользу вершин множеств 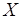 или
или 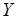 в зависимости от того, где больше (меньше) суммарная длительность операций. В рассматриваемом примере дополнительный ресурс вводится для операций, представленных вершинами
в зависимости от того, где больше (меньше) суммарная длительность операций. В рассматриваемом примере дополнительный ресурс вводится для операций, представленных вершинами 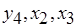 . Коэффициент использования двух базовых процессоров в этом случае составляет
. Коэффициент использования двух базовых процессоров в этом случае составляет 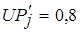 (см. рис. 6.12, б и 6.13, в). Такое приближенное разрешение коллизий возможно за время нахождения компонент связности в графе "многослойных" коллизий, т.е.
(см. рис. 6.12, б и 6.13, в). Такое приближенное разрешение коллизий возможно за время нахождения компонент связности в графе "многослойных" коллизий, т.е. 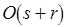 , если использовать метод поиска в глубину.
, если использовать метод поиска в глубину.
Оценим временную сложность процедур разрешения коллизий как функцию от числа 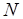 масштабируемых операций. Приближенное разрешение коллизий имеет порядок
масштабируемых операций. Приближенное разрешение коллизий имеет порядок  , поскольку
, поскольку 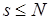 ,
, 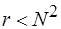 . При условно оптимальном разрешении – это оценка порядка
. При условно оптимальном разрешении – это оценка порядка 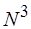 в силу того, что
в силу того, что 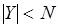 . При этом порядок сложности не увеличивается, если учитывать все экземпляры доступных ресурсов для каждой операции.
. При этом порядок сложности не увеличивается, если учитывать все экземпляры доступных ресурсов для каждой операции.
Погрешность планирования. Часть операций обмена данными может быть исключена, если информационно связанные операции обработки последовательно выполняются на одном и том же процессоре. Так, в рассматриваемом примере (см. рис. 6.12) нет необходимости в затратах на обмен данными в заданиях 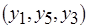 ,
, 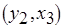 и
и 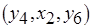 , поскольку входящие в них операции обработки реализуются соответственно на первом, втором (базовых) и третьем (дополнительном) процессорах. Напомним, что значения длительности всех необходимых операций обмена одинаковы и равны 0,5 единиц времени (см. рис. 6.12, б). Ни в одной из трех работ, которым соответствуют последовательности операций обработки
, поскольку входящие в них операции обработки реализуются соответственно на первом, втором (базовых) и третьем (дополнительном) процессорах. Напомним, что значения длительности всех необходимых операций обмена одинаковы и равны 0,5 единиц времени (см. рис. 6.12, б). Ни в одной из трех работ, которым соответствуют последовательности операций обработки 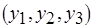 ,
, 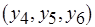 и
и 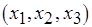 , затраты на обмен данными исключены быть не могут, поскольку каждая из двух последовательно выполняемых операций обработки данных назначается на разные экземпляры процессоров. Тем не менее из рис. 6.12, б видно, что время, отведенное для выполнения операции
, затраты на обмен данными исключены быть не могут, поскольку каждая из двух последовательно выполняемых операций обработки данных назначается на разные экземпляры процессоров. Тем не менее из рис. 6.12, б видно, что время, отведенное для выполнения операции 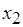 , может быть увеличено на 0,5 единиц, что позволяет повысить коэффициент использования третьего процессора и, в целом, процессоров данного типа. Однако изменение промежуточного или окончательного плана некоторых процессов обработки после исключения затрат на обмен может привести к необходимости заново проводить масштабирование других, ранее спланированных операций. Поэтому для обеспечения сходимости алгоритмов масштабирования приходится смириться с погрешностью планирования информационно связанных операций обработки, для которых исключаются затраты на обмен. Погрешность обусловлена "недоиспользованием" процессами обработки данных возможного времени их выполнения.
, может быть увеличено на 0,5 единиц, что позволяет повысить коэффициент использования третьего процессора и, в целом, процессоров данного типа. Однако изменение промежуточного или окончательного плана некоторых процессов обработки после исключения затрат на обмен может привести к необходимости заново проводить масштабирование других, ранее спланированных операций. Поэтому для обеспечения сходимости алгоритмов масштабирования приходится смириться с погрешностью планирования информационно связанных операций обработки, для которых исключаются затраты на обмен. Погрешность обусловлена "недоиспользованием" процессами обработки данных возможного времени их выполнения.
Пусть 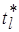 и
и 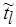 – значения суммарного времени обработки в
– значения суммарного времени обработки в 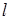 -й работе, где
-й работе, где 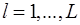 , соответственно при оптимальном и "приближенном" планировании с погрешностью. Обозначим через
, соответственно при оптимальном и "приближенном" планировании с погрешностью. Обозначим через 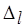 время для обмена данными в
время для обмена данными в 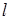 -й работе, а через
-й работе, а через  и
и 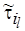 – оптимальное и "приближенное" значения длительности
– оптимальное и "приближенное" значения длительности 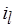 -й операции обработки. При этом
-й операции обработки. При этом 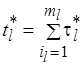 ,
,  ,
, 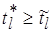 , где
, где 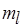 – число операций обработки. Однако это не означает, что
– число операций обработки. Однако это не означает, что 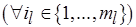
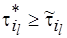 , поскольку выбирается оптимальный план для всей совокупности процессов обработки в
, поскольку выбирается оптимальный план для всей совокупности процессов обработки в 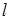 -й работе, а не для каждой из операций в отдельности (см. п. 6.2).
-й работе, а не для каждой из операций в отдельности (см. п. 6.2).
Относительная погрешность масштабирования 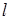 -й работы составляет
-й работы составляет
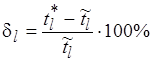 . (6.33)
. (6.33)
Отклонение полученного в результате масштабирования плана от оптимального для всей системы из 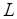 работ будем оценивать усредненной относительной погрешностью вида
работ будем оценивать усредненной относительной погрешностью вида
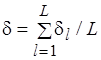 , (6.34)
, (6.34)
где 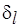 определяется в соответствии с (6.33).
определяется в соответствии с (6.33).
Положим, что ограничения в задаче масштабирования, заданные в виде неравенств, содержащих, в частности, крайние сроки завершения процессов и всей программы, являются связывающими. Напомним, это означает, что эти неравенства обращаются в равенства при тех значениях независимых переменных масштабирования, когда соответствующий критерий достигает экстремума.
Пусть для суммарного времени обмена выполняется неравенство
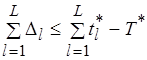 , (6.35)
, (6.35)
где 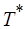 – крайний срок завершения программы.
– крайний срок завершения программы.
Очевидно, что правая часть (6.35) – неотрицательная величина. Тогда имеет место следующая оценка сверху усредненной относительной погрешности (6.34):
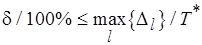 . (6.36)
. (6.36)
Действительно, 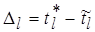 и
и 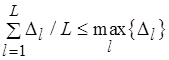 . При этом из (6.35) следует, что
. При этом из (6.35) следует, что 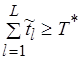 . Это и означает, что справедливо (6.36).
. Это и означает, что справедливо (6.36).
В рассматриваемом примере (см. рис. 6.12) 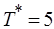 ;
; 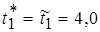 ;
;  ;
; 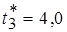 , а
, а 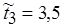 . Соответствующие значения относительной погрешности масштабирования трех работ равны:
. Соответствующие значения относительной погрешности масштабирования трех работ равны: 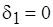 ;
; 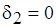 ;
;  . Усредненная относительная погрешность по системе из трех работ составляет
. Усредненная относительная погрешность по системе из трех работ составляет 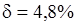 . Далее,
. Далее, 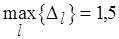 , что соответствует третьей работе (см. рис. 6.12, б). Выполняется неравенство (6.35), поскольку
, что соответствует третьей работе (см. рис. 6.12, б). Выполняется неравенство (6.35), поскольку 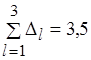 , а
, а 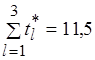 . Следовательно, справедливо и (6.36):
. Следовательно, справедливо и (6.36): 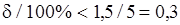 .
.
Таким образом, когда для процессов обмена данными выполняется условие (6.35), верхняя граница усредненной относительной погрешности планирования после разрешения коллизий определяется максимумом отношения длительности обмена по отдельным работам к крайнему сроку завершения программы (6.36).
КРАТКАЯ СВОДКА НЕОБХОДИМЫХ СВЕДЕНИЙ ПО КОМБИНАТОРИКЕ И ТЕОРИИ ГРАФОВ. Основной математический аппарат, который используется в этой главе, это – потоки в сетях и связанные с ними задачи [3], а также теория матроидов и жадные алгоритмы [1, 2]. Именно по этим разделам теории графов и комбинаторики ниже приводится минимум сведений, которые нужны для понимания отдельных этапов синтеза целевой архитектуры.
Существует целый ряд алгоритмов поиска на графах, использующих систематический просмотр вершин, когда каждая из них анализируется лишь однажды. Один из методов, использующихся в таких алгоритмах, называется поиском в ширину. Его основная идея заключается в следующем. Выбирается произвольная вершина 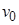 графа
графа 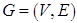 с множеством
с множеством  вершин и множеством
вершин и множеством 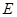 дуг. Определяются все вершины-соседи, т.е. вершины, находящиеся от
дуг. Определяются все вершины-соседи, т.е. вершины, находящиеся от 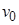 на расстоянии в одну дугу. Произвольно выбирается вершина
на расстоянии в одну дугу. Произвольно выбирается вершина 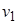 из окружения вершины
из окружения вершины 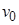 и рассматривается окружение
и рассматривается окружение 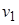 . Процесс продолжается до тех пор, все вершины графа
. Процесс продолжается до тех пор, все вершины графа 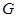 не будут просмотрены.
не будут просмотрены.
При поиске в глубину просмотр также начинается с некоторой произвольной вершины 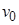 . Затем просматривается какая-либо вершина
. Затем просматривается какая-либо вершина 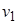 , смежная с
, смежная с 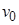 , и процесс повторяется от вершины
, и процесс повторяется от вершины 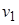 . Если не существует вершин смежных с
. Если не существует вершин смежных с 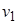 , то осуществляется возврат к
, то осуществляется возврат к 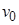 и выбирается другая, смежная с ней вершина. Таким образом, в отличие от поиска в ширину, поиск в глубину от вершины
и выбирается другая, смежная с ней вершина. Таким образом, в отличие от поиска в ширину, поиск в глубину от вершины 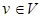 основан на просмотре всех вершин, смежных с
основан на просмотре всех вершин, смежных с 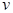 .
.
Для определения трудоемкости, или сложности, алгоритма часто используют 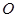 -символику. Говорят, что неотрицательная функция
-символику. Говорят, что неотрицательная функция 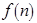 , где
, где 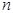 – размерность входа (натуральное число), не превосходит по порядку функцию
– размерность входа (натуральное число), не превосходит по порядку функцию 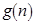 , если существуют такие константы
, если существуют такие константы 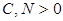 , что
, что 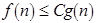 для всех
для всех 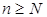 . При этом используется запись
. При этом используется запись 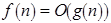 . Запись
. Запись 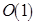 означает, что сложность алгоритма не зависит от размерности входа. В такой символике временная сложность (число шагов) многих алгоритмов, использующих методы поиска в ширину или глубину, составляет
означает, что сложность алгоритма не зависит от размерности входа. В такой символике временная сложность (число шагов) многих алгоритмов, использующих методы поиска в ширину или глубину, составляет 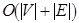 .
.
Сетью обычно называют произвольный ориентированный граф 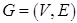 , каждой дуге которого некоторая функция (поток) ставит в соответствие неотрицательное вещественное число, называемое пропускной способностью дуги. В сети выделяются две вершины – источник
, каждой дуге которого некоторая функция (поток) ставит в соответствие неотрицательное вещественное число, называемое пропускной способностью дуги. В сети выделяются две вершины – источник 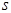 и сток
и сток 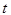 . Величину, равную сумме весов дуг, исходящих из источника
. Величину, равную сумме весов дуг, исходящих из источника 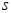 или входящих в сток
или входящих в сток 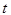 , называют величиной потока. Поток не возникает и не накапливается ни в одной из вершин
, называют величиной потока. Поток не возникает и не накапливается ни в одной из вершин 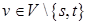 . Алгоритмы построения потока с максимальной величиной (максимального потока), как правило, основываются на последовательном увеличении потока.
. Алгоритмы построения потока с максимальной величиной (максимального потока), как правило, основываются на последовательном увеличении потока.
Произвольное подмножество 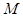 попарно несмежных ребер неориентированного графа называется паросочетанием. Паросочетание является наибольшим, если число ребер в нем наибольшее среди всех паросочетаний графа. В двудольном графе
попарно несмежных ребер неориентированного графа называется паросочетанием. Паросочетание является наибольшим, если число ребер в нем наибольшее среди всех паросочетаний графа. В двудольном графе 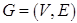 множество вершин
множество вершин 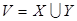 можно разбить на непересекающиеся подмножества
можно разбить на непересекающиеся подмножества 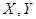 , а каждое ребро
, а каждое ребро 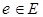 имеет вид
имеет вид 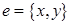 , где
, где 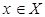 ,
, 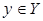 . Задачу нахождения наибольшего паросочетания в таком графе
. Задачу нахождения наибольшего паросочетания в таком графе 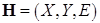 можно свести к поиску максимального потока в сети
можно свести к поиску максимального потока в сети 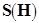 , построенной на этом графе. Существует взаимно однозначное соответствие между
, построенной на этом графе. Существует взаимно однозначное соответствие между