Принцип оптимальности впервые былсформулирован Ричардом Беллманом в 1953 г. Каково бы ни было состояние S системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.
Отметим, что эта формулировка принципа несколько отличается от исходной, сформулированной Беллманом и дана Е. С. Вентцель.
Беллманом сформулированы и условия, при которых принцип верен. Основное требование - процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги.
Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом. Если изобразить геометрически оптимальную траекторию в виде ломаной линии, то любая часть этой ломаной будет являться оптимальной траекторией относительно начала и конца.
Уравнения Беллмана. Вместо исходной задачи динамического программирования с фиксированным числом шагов п и начальным состоянием S0 рассмотрим последовательность задач, полагая последовательно п=1, 2,... при различных S - одношаговую, двухшаговую и т. д., используя принцип оптимальности.
Введем ряд новых обозначений. Обозначения в ДП несут большую информационную нагрузку, поэтому очень важно их четко усвоить..
На каждом шаге любого состояния системы Sk-1 решение Xk необходимо выбирать «с оглядкой», так как этот выбор влияет на последующее состояние Sk и дальнейший процесс управления, зависящий от Sk. Это следует из принципа оптимальности.
Вместе с тем, имеется один шаг, последний, который можно для любого состояния Sn-1 планировать локально-оптимально, исходя только из соображений этого шага. Поэтому, как правило, задачи методом динамического программирования решаются по обратной схеме (с последнего состояния)
Рассмотрим n-й шаг: S n-1 - состояние системы к началу n-го шага, S n= Si - конечное состояние, Хп - управление на n-м шаге, fn(Sn-1, Хn) - целевая функция (выигрыш) n-го шага.
Согласно принципу оптимальности, Хn нужно выбирать так, чтобы для любых состояний Sn-1 получить максимум целевой функции на этом шаге (будем для конкретности рассматривать только задачу максимизации).
Обозначим через Zn*(Sn-1) максимум целевой функции показателя эффективности n-го шага при условии, что к началу последнего шага система S была в произвольном состоянии Sn-1, а на последнем шаге управление было оптимальным.
Zn*(Sn-1) называется условным максимумом целевой функции на n-м шаге. Очевидно, что
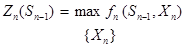(4.5)
Максимизация ведется по всем допустимым управлениям Хn.
Решение Хn, при котором достигается Zn*(Sn-1), также зависит от Sn-1 и называется условным оптимальным управлением на n-м шаге. Оно обозначается через Xn* (Sn-1).
Решив одномерную задачу локальной оптимизации по уравнению (4.5), определим для всех возможных состояний Sn-1 две функции: Zn*(Sn-1) и Xn* (Sn-1).
Рассмотрим теперь двухшаговую задачу: присоединим к n-му шагу (п-1)-й (рисунок 4.2).
Для любых состояний Sn-2, произвольных управлений Xn-1 и оптимальном управлении на п-м шаге значение целевой функции на двух последних шагах равно:
fn-1(Sn-2, Xn-1)+ Z (Sn-1) ( 4.6)
Согласно принципу оптимальности для любых Sn-2 решение нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем (n-м) шаге приводило бы к максимуму целевой функции на двух последних шагах. Следовательно, нужно определить максимум выражения (13.6) по всем допустимым управлениям Xn-1. Максимум этой суммы зависит от Sn-2, обозначается через Z*n-I (Sn-2) и называется условным максимумом целевой функции при оптимальном управлении на двух последних шагах.
Соответствующее управление Хп-l на (п-1)-м шаге обозначается через Хп-l (Sn-2) и называется условным оптимальным управлением на (п-1)-м шаге.
(4.7)
Следует обратить внимание на то, что выражение, стоящее в фигурных скобках (4.7), зависит только от Sn-2 и Xn-1, так как Sn-1 можно получить из уравнения состояний (4.2) при k = n-1
Sп-1 = φn-1(Sn-2, Xn1l)
и подставить вместо Sn-1 в функцию Z*n (Sn-1).
В результате максимизации только по одной переменной Хп-1 согласно уравнению (13.7) вновь получаются две функции:
Z*n-l (Sn-2) и Х*п1 (Sn-2).
Далее рассматривается трехшаговая задача: к двум последним шагам присоединяется (п-2)-й и т.д.
Обозначим через Z*k (Sk-1) - условный максимум целевой функции, полученный при оптимальном управлении на n – k + 1 шагах, начиная с k- го до конца, при условии, что к началу k-го шага система находилась в состоянии Sk-. Фактически эта функция равна
Z*k (Sk-1) = max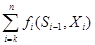 
.
{Xk,…,Xn}
Тогда Z*k+ 1 (Sk) = max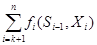 
.
{Xk+1,…,Xn}
Целевая функция на n – k последних шагах (рисунок 4.1) при произвольном управлении Xk на k- м шаге и оптимальном управлении на последующих n – k шагах равна fk(Sk-1, Xk) + Z*k+1 (Sk).
|
 |
Рисунок 4.2 - Пояснение к получению выражения для целевой функции
Согласно принципу оптимальности, Xk выбирается из условия максимума этой суммы, т.е.
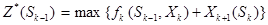, k = n-1, n-2,…,2,1. (4.8)
{Хk}
Управление Xk на k-м шаге, при котором достигается максимум в (4.8), обозначается через Х*(Sk-1) и называется условным оптимальным управлением на k-м шаге (в правую часть уравнения (13.8) следует вместо Sk подставить выражение Sk = φk(Sk-1,Xk), полученное из уравнений состояния).
Уравнения (4.8) называют уравнениями Беллмана. Это рекуррентные соотношения, позволяющие получить предыдущее значение функции, зная последующие.
Если из (4.5) получить Z*n(Sn-1), то при k = n-1 из (13.8) можно определить, решив задачу максимизации, решив для всех возможных значений Sn-2, выражения для Z*n-1 (Sn-2) и соответствующее Хп-1 (Sn-2).
Далее, зная Z*n-1 (Sn-2), получаем, используя (4.8) и (4.2), уравнения состояний.
Процесс решения уравнений (4.5) и (4.8) называется условной оптимизацией. В данном случае рассмотрен способ решения задачи динамического программирования, начиная с последнего шага (так называемая «обратная схема»). В принципе можно n-1 и 1-й шаги поменять местами и это будет, так называемая «прямая схема».
В результате условной оптимизации получаются две последовательности:
Z*n(Sn-1), Z*n-1(Sn-2),..., Z*2(S1), Z*1(S0)
условные максимумы целевой функции на последнем, на двух последних, на ...п шагах и
X *n(Sn-1), X*n-1(Sn-2),..., X *2(S1), X*1(S0)
условные оптимальные управления на п-м, (п-1)-м,..., l-м шагах.
Используя эти последовательности, можно получить решение задачи динамического программирования при данных п и S0.
По определению Z*1 (S0) - условный максимум целевой функции за п шагов при условии, что к началу l-го шага система была в состоянии S0, т.е.
Zmax = Z*(S0). (4.9)
Далее следует использовать последовательность условных оптимальных управлений и уравнения состояний (13.2).
При фиксированном S0 получаем Х*1 = Х*1 (S0). Далее из уравнений (4.2) получаем S1= φ1(S0',X*1) и подставляем это выражение в последовательность условных оптимальных управлений: Х*2 = Х*2 (S1) и т.д.по цепочке:
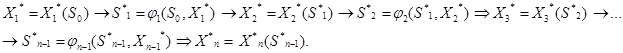
В результате получается оптимальное решение задачи динамического программирования X* = (X*1, X*2,…, X*n).
В приведенной цепочке используются следующие обозначения:
→ - использование уравнений состояния;
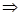- использование последовательности условных оптимальных управлений;
Sk - состояние системы после k-го шага при условии, что на k- м шаге выбрано оптимальное управление.
Задание 2. Задача оптимального распределения инвестиций (освоить метод решения задачи)
Планируется деятельность четырех предприятий, входящих в единую корпорацию на 1 год. Начальные инвестиционные средства составляют 5 усл. ед. Инвестиции могут вноситься в каждое предприятие трансфертами кратными одной условной единице. Средства, вложенные в каждое отдельное предприятие, приносят в конце года прибыль Fi(Х), заданную таблично (таблица 4.1)
Таблица 4.1- Исходные данные
| Количество вложенных средств -Х | Прибыль от первого предприятия F1(X) | Прибыль от второго предприятия F2(X) | Прибыль от третьего предприятия F3(X) | Прибыль от четвертого предприятия F4(X) |
Требуется так распределить инвестиции, чтобы общая прибыль корпорации за год была бы максимальной.
Известны следующие условия:
- функция прибыли для данного предприятия Fi(Х) не зависит от того, сколько средств вложено в остальные предприятия корпорации;
- прибыль данного предприятия Fi(Х) в конце каждого года зависит только от того, сколько средств вложено в данное предприятие в начале этого года и не зависит от того, сколько средств было вложено в данное предприятие в предыдущие годы;
- прибыль от каждого предприятия исчисляется в одних и тех же условных единицах;
- общая прибыль корпорации является аддитивной функцией от прибылей всех предприятий корпорации.
Решение. Составим экономико-математическую модель:
- целевая функция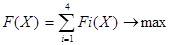 
;
- ограничения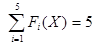 
.
Анализ экономико-математической модели позволяет сделать следующие выводы:
- целевая функция линейна, ограничения – линейны и задачу можно было бы решить симплекс – методом, но у задачи есть важная особенность – целевая функция задана таблично;
- так как вкладываемые средства кратны одной условной единице (дискретно), то исследуемый процесс является дискретным по состояниям:
- так как средства вкладываются только в начале каждого года, то данный процесс является дискретным и во времени.
С учетом этих условий задачу целесообразно решать методом динамического программирования.
Формально будем решать задачу методом косоугольных таблиц, начиная с двух последних предприятий (рисунок 4. 3).
Задача решается в два этапа: этап 1 – этап условно-оптимальных распределений; этап 2 – этап оптимального распределения инвестиций.
Этап 1 - этап условно-оптимальных распределений. Этап выполняется от последнего предприятия к первому (обратная схема).
Фазовыми состояниями в задаче являются значения прибыли объединения к концу года F(X), а управлениями – выделяемые каждому предприятию инвестиции х = 0,1.2, 3. 4, 5.
По правой стороне таблицы запишем в клетки таблицы значения прибыли от инвестиций, вложенных в предприятие 4 (F4(X)), изменяя Х от 0 до 5 (из таблицы 4.1).
. По левой стороне таблицы запишем в клетки таблицы значения прибыли от инвестиций, вложенных в предприятие 3 (F3(X)), изменяя Х от 0 до 5 (из таблицы 4.1).
Остальные клетки таблицы заполняем числами, равными сумме F3(X) + F4(X), при изменении Х от 0 до 5.
Так, если в предприятие 3 будет инвестирована 1 у. е. и в предприятие 4 тоже 1 у.е., то прибыль в конце года будет составлять
F(1,1) = 5 + 6 = 11 у.е.
Аналогично, если в предприятие 3 будут инвестированы 3 у. е. и в предприятие 4 - 2 у.е., то прибыль в конце года будет составлять
F(1,1) = 11 + 7 = 18 у.е.
Далее, так как наша цель получение наибольшей прибыли, то в каждой строке матрицы мы должны выбрать наибольший элемент. Так если мы примем, что будем инвестировать в предприятия 3 или 4 - по одной у.е., то общая прибыль будет определяться из условия
F(X(1,1)) = max { 5;6} = 6 (выделено в таблице 4.2 цветом и подчеркиванием).
Если мы примем, что будем инвестировать в предприятия 3 или 4 две у.е., то общая прибыль будет определяться из условия
- предприятию 3 - 2 у.е., предприятию 4 – 0 у.е. → 9;
- предприятию 3 - 1 у.е., предприятию 4 – 1 у.е. → 11;
- предприятию 3 - 0 у.е., предприятию 4 – 2 у.е. → 7.
Естественно, необходимо выбрать вариант - предприятию 3 - 1 у.е., предприятию 4 – 1 у.е. → 11 (выделен цветом и подчеркиванием).
Применение косоугольных таблиц позволяет формально рассчитать все возможные варианты и выбрать из них оптимальные (6; 11; 15; 17; 18).
После этого переходят к построению второй косугольной таблицы (таблица 4.3, рисунок 4.4).
 |
Рисунок 4.3- Таблица 4.2
По правой стороне таблицы записываем числа, соответствующие оптимальным значениям распределения инвестиций между предприятиями 3 и 4 ((6; 11; 15; 19; 22) (max F3(X) + F4(X)).
По левой стороне таблицы запишем в клетки значения прибыли от инвестиций, вложенных в предприятие 2 (F2(X)), изменяя Х от 0 до 5 из таблицы 4.1.
Остальные клетки таблицы заполняем аналогично тому, как выполняли при заполнении таблицы 4.2.
Далее, также как на предыдущем шаге в каждой строке таблицы выделяем максимальный элемент (цветом и подчеркиванием).
Переходим к следующему шагу (построению таблицы 4.4, рисунок 4.5). все действия осуществляются по аналогии с предыдущим шагом.
 |
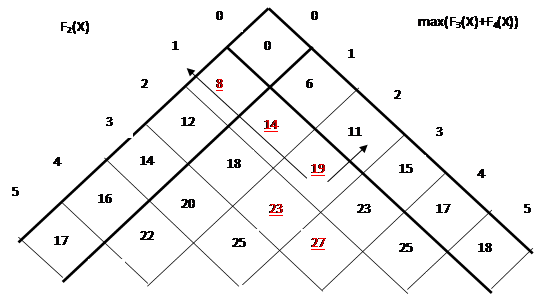Рисунок 4.4 -Таблица 4.3
 |
Рисунок 4.5- Таблица 4.4
На этом заканчивается первый этап решения задачи – этап получения условно-оптимальных распределений.
Этап 2. Этап распределения инвестиций. Этап выполняется от первого состояния к последнему.
В последней строке последней таблицы (в данной задаче – таблица 4.4) отыскиваем максимальный элемент – это 33. Это число выполняет две функции:
- первая – это максимально возможное получение объединением прибыли;
- вторая – отправная точка (фазовое состояние) распределения инвестиций.
От клетки со значением F*(X*) = 33 движемся в северо-западном направлении до левой стороны таблицы. Эта выделенная полоса таблицы приводит к цифре 2, которая означает, что для того, чтобы получить максимум прибыли, необходимо в предприятие 1 инвестировать 2 у.е.
Это даст объединению 12 у.е. прибыли.
Следовательно, остальные (5 – 2 = 3) у.е. должны быть инвестированы в оставшиеся 2, 3 и 4 –е предприятия. Для получения конкретных управлений от той же клетки со значением 33 движемся в северо-восточном направлении до правой стороны таблицы, приходим к значению 19. Это означает, что оставшиеся три предприятия (2, 3 и 4 –е) должны вместе дать 19 у.е. прибыли.
По числу 19 входим в предыдущую таблицу (таблица 4.3). Число 19 находится в третьей строке таблицы. От клетки со значением F*(X*) = 19 движемся в северо-западном направлении до левой стороны таблицы. Эта выделенная полоса таблицы приводит к цифре 1, которая означает, что для того, чтобы получить максимум прибыли, необходимо в предприятие 2 инвестировать 1 у.е. Это даст объединению 8 у.е. прибыли.
Следовательно, остальные (5 – 2 -1 = 2) у.е. должны быть инвестированы в оставшиеся 3 и 4 –е предприятия. Для получения конкретных управлений от той же клетки со значением 19 движемся в северо-восточном направлении до правой стороны таблицы, приходим к значению 11. Это означает, что оставшиеся два предприятия (3 и 4 –е) должны вместе дать 11 у.е. прибыли.
По числу 11 входим в предыдущую таблицу (таблица 4.2). Число 11 находится во второй строке таблицы. От клетки со значением F*(X*) = 11 движемся в северо-западном направлении до левой стороны таблицы. Эта выделенная полоса таблицы приводит к цифре 1, которая означает, что для того, чтобы получить максимум прибыли, необходимо в предприятие 3 инвестировать 1 у.е. Это даст объединению 5 у.е. прибыли. Двигаясь от клетки со значением 11 в северо-восточном направлении приходим к выводу, что в предприятие 4 необходимо инвестировать 1 у.е. Это даст объединению 6 у.е. прибыли.
Таким образом, решением задачи является вектор: Х* = (2, 1, 1, 1). При этом прибыль объединения составит 31 у.е.
Это же значение целевой функции можно получить из таблицы 4.1, выбрав соответствующие управлениям значения х1* = 2 → 12 у.е.; х2* = 1 → 8 у.е.; х3* = 1 → 5 у.е.; х4* = 1 → 6 у.е..
Откуда F*(X*) = 12 + 8 + 5 + 6 = 31 у.е.
Практическая часть
Задание 3. Решить задачу методом динамического программирования (самостоятельно по вариантам).
Планируется деятельность пяти предприятий, входящих в единое объединение на 1 год. Начальные инвестиционные средства составляют 600 усл. ед. Инвестиции могут вноситься в каждое предприятие трансфертами кратными 100 условных единиц. Средства, вложенные в каждое отдельное предприятие, приносят в конце года прибыль Fi(Х), заданную таблично (по вариантам).
Требуется так распределить инвестиции по предприятиям, чтобы общая прибыль объединения за год была бы максимальной.
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2021-12-14 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд