Построить кривую.
| 5в | 4x2-y2-32x+48=0 |
Решение:
 4x2-y2-32x+48=0
4x2-y2-32x+48=0


 - получили каноническое уравнение гиперболы с полуосями
- получили каноническое уравнение гиперболы с полуосями 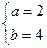
Здесь  .
.
Строим кривую:

Задание 3 Решить систему линейных уравнений 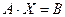 методом последовательного исключения неизвестных, выяснив предварительно вопрос о ее совместности с помощью теоремы Кронекера-Каппели. В случае неопределенности системы найти ее общее, базисное и любое частное решение.
методом последовательного исключения неизвестных, выяснив предварительно вопрос о ее совместности с помощью теоремы Кронекера-Каппели. В случае неопределенности системы найти ее общее, базисное и любое частное решение.
5 в) 
Решение:
Запишем расширенную матрицу системы:

Находим ранг (не расширенной) матрицы системы
Поскольку правый верхний определитель отличен от нуля,

Ранг матрицы системы равен 4 (больше он быть не может, так как всего 4 строки в системе). По этой же причине, ранг расширенной матрицы системы также равен 4. По теореме Кронекера-Капелли, система совместна.
Решаем систему методом последовательного исключения неизвестных:
Из первого уравнения выразим 
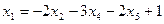 ;
;
Подставим во второе уравнение и выразим в нём 

 ;
;
Подставим оба эти выражения в 3 –ее уравнение
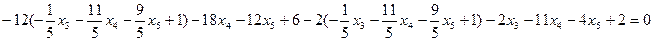
После приведения подобных и умножения на 5, получим:
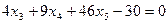

Подставляем это в выражения для  получаем:
получаем:
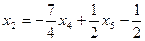 ;
;
 ;
;
Подставляем эти 3 выражения в последнее уравнение

После приведения подобных и умножения на 4, получим:

 ;
;
Подставляя это в выражения для остальных переменных, получаем общее решение
(выбрали свободной переменной  )
)

Подставив  , получим фундаментальное решение:
, получим фундаментальное решение:

Чтобы получить какое-нибудь частное решение, положим  и получим:
и получим:

Задание 4 Доказать совместность системы линейных уравнений и решить ее по методу Крамера и матричным способом.
65в. 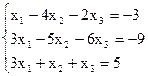
Решение:
Считаем главный определитель системы:
 система совместна и имеет единственное решение.
система совместна и имеет единственное решение.
Находим его методом Крамера:
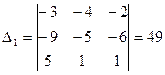 ;
;  0;
0;  ;
;
 ;
;  ;
;  ;
;  .
.
Теперь находим то же решение матричным методом.
Для этого обращаем матрицу системы
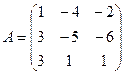 . Считаем алгебраические дополнения:
. Считаем алгебраические дополнения:
 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
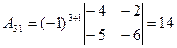 ;
;  ;
; 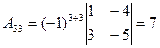 ;
;
Получаем обратную матрицу:
 .
.
Умножаем на неё правую часть слева и получаем решение:
 - сошлось.
- сошлось.
Задание 5 Коллинеарны ли векторы 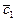 ,
,  . Перпендикулярны ли векторы
. Перпендикулярны ли векторы  ,
,  , если
, если  =
= 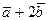 ;
;  = 3
= 3 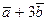 ;
;  =
= 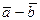 ;
;  = 2
= 2 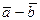

| 
| |
| 5в | 
| 
|
Решение:
Записываем координаты рассматриваемых векторов:


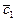 =
= 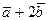 =
= 
 = 3
= 3 
Видим, что координаты этих векторов не пропорциональны:
 вектора
вектора  ,
,  не коллинеарны.
не коллинеарны.
 =
=  ;
;
 = 2
= 2 

Находим скалярное произведение:
 вектора
вектора  ,
,  не перпендикулярны.
не перпендикулярны.
Задание № 6 (пирамиды) Даны координаты вершин пирамиды АВСD. Требуется:
1. Записать векторы  в системе орт и найти модули этих векторов.
в системе орт и найти модули этих векторов.
2. Найти угол между векторами  .
.
3. Найти площадь грани АВС.
4. Найти объем пирамиды.
5. Найти каноническое уравнение прямой, проходящей через точку D перпендикулярно плоскости АВС.
6. Найти точки пересечения полученной прямой с плоскостью АВС и с координатными плоскостями хОу; хОz; уОz.
7. Найти уравнение плоскости, проходящей через точку D и С и перпендикулярно плоскости АВС.
8. Длину ребра АВ;
9. Длину высоты пирамиды, проведенной из вершины D;
10. Уравнение ребра АС.
| 5в | А(-1, 1,-5); В(3,5,-7); С(1,12,-15) D (-1,3,-4) |
Решение:
1)
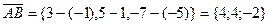 ;
;

 ;
;
 ;
;
 ;
;
 ;
;
2) Обозначим искомый угол  .
.

3)
 ;
;

4)

5)
Находим уравнение плоскости  . Ищем в общем виде
. Ищем в общем виде
 , поскольку ясно, что через начало координат она не проходит, полагаем
, поскольку ясно, что через начало координат она не проходит, полагаем  . Подставляем в эту систему координаты точек
. Подставляем в эту систему координаты точек  , получаем систему на коэффициенты и решаем её.
, получаем систему на коэффициенты и решаем её.




(умножили на -7)
Искомая прямая имеет направляющим вектором нормаль к этой плоскости  , и проходит через точку
, и проходит через точку 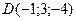 . Записываем её уравнение:
. Записываем её уравнение:
 .
.
6)
Перепишем полученное в предыдущем пункте уравнение прямой в параметрическом виде:
 .
.
Чтобы найти точку пересечения этой прямой с плоскостью
 , подставляем это параметрическое представление прямой в уравнение плоскости
, подставляем это параметрическое представление прямой в уравнение плоскости
 ;
;  , где
, где
 ,
, 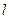 - рассматриваемая прямая.
- рассматриваемая прямая.
Аналогично находим точки пересечения этой прямой с координатными плоскотями.
 ;
;
 ;
;
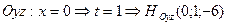 .
.
7)
Пусть уравнение искомой плоскости

Подставляем условия перпендикулярности плоскости  и точки
и точки


Тут тоже легко видеть, что  не подходит (получаются нулевые коэффициенты). Полагаем
не подходит (получаются нулевые коэффициенты). Полагаем  . Подставляем и решаем полученную систему. Получаем:
. Подставляем и решаем полученную систему. Получаем:

Умножив все коэффициенты на 71, получи уравнение искомой плоскости:

8)  ;
;
9)В пункте 4 мы нашли объем пирамиды, а в пункте 3 площадь грани 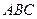 . Воспользуемся этим
. Воспользуемся этим
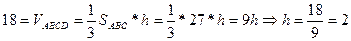
10) ребро  проходит через точку А(-1, 1,-5) и имеет направляющий вектор
проходит через точку А(-1, 1,-5) и имеет направляющий вектор
 .
.
Записываем его уравнение:

Рекомендуемая основная литература
1. Высшая математика для экономистов / Под ред. Н.Ш. Кремера.- 3-е изд. - М.: ЮНИТИ, 2007. - 479 с. - (Золотой фонд Российских учебников) - ISBN 5-238-00991-7.
2. Красс, М.С. Математика для экономического бакалавриата: Учебник/ М.С. Красс, Б.П. Чупрынов. - М.: Дело, 2005. - 576 с - ISBN 5-7749-0404-0.
3 Красс, М. С. Математика для экономистов: учеб.пособие для вузов/ М. С. Красс, Б.П. Чупрынов. - CПб.: Питер, 2005. - 464 с. - (Учебное пособие). - Библиогр.: с. 461. - Предм.указ.: с. 462-464. - ISBN 5-94723-672-9.
3. Солодовников, А.С. Математика в экономике: учеб.для вузов / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов. - М.: Финансы и статистика, 1998. - 224с - ISBN 5-279-01943-7.
4. Математика в экономике: учеб.для вузов / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов,И.Г. Шандра. - М.: Финансы и статистика, 1999. - 376с - ISBN 5-279-01944-5.
5. Высшая математика для экономистов / Под ред. Н.Ш. Кремера.- 2-е изд., перераб. и доп.. - М.: ЮНИТИ, 2002. - 471 с - ISBN 5-238-00030-8.
6. Экономико-математическое моделирование: учебник / Под ред. И.Н. Дрогобыцкого. - М.: ЭКЗАМЕН, 2006. - 798 с - ISBN 5-472-01573-1.
7. Экономико-математические методы и прикладные модели: учеб.пособие для вузов/ под ред.В.В. Федосеева. - М.: ЮНИТИ, 2002. - 391 с - ISBN 5-238-00068-5.
Дополнительная литература
1. Акулич, И.Л. Математическое программирование в примерах и задачах: учеб. пособие / И.Л. Акулич.- 2-е изд., испр. - CПб.: Лань, 2009. - 347 с. - Библиогр.: с. 346-347. - ISBN 978-5-8114-0916-7.
2. Пантелеев, А.В. Методы оптимизации в примерах и задачах / А.В. Пантелеев, Т.А. Летова. - М.: Высшая школа, 2002. - 544с - ISBN 5-06-004137-9.
3. Коршунова, Н.И. Математика в экономике: учеб. пособ / Н.И. Коршунова, В.С. Плясунов. - М.: Вита-Пресс, 1996. - 368с - ISBN 5-7755-0012-1.
4. Плис, А.И. Mathcad. Математический практикум для инженеров и экономистов: Учеб. пособие / А.И. Плис, Н.А. Сливина.- 2-е изд., доп. и перераб. - М.: Финансы и статистика, 2003. - 656 с.: ил. - ISBN 5-279-02550-Х.
5. Шелобаев, С. И. Математические методы и модели в экономике, финансах, бизнесе: учеб. пособие для вузов/ С.И. Шелобаев. - М.: ЮНИТИ-ДАНА, 2001. - 367 с.
8. Замков, О. О. Математические методы в экономике: учебник / О. О. Замков, А. В. Толстопятенко, Ю. Н. Черемных; общ. ред. А. В. Сидорович.- 4-е изд. стер. - М.: Дело и Сервис, 2004. - 368 с. - (Учебники МГУ им. М. В. Ломоносова) - ISBN 5-86509-054-2.
9. Замков, О.О. и др. Математические методы в экономике. Учебник. 3-е изд. перераб. /Под ред. А.В. Сидоровича.- М.: Дело и Сервис, 2011
10. Лабскер, Л. Г. Игровые методы в управлении экономикой и бизнесом: учеб. пособие для вузов / Л. Г. Лабскер, Л. О. Бабешко; Акад. нар. хоз-ва при Правительстве РФ. - М.: Дело, 2001. - 464 с - ISBN 5-7749-0233-1.
11. Гашков, С.Б. Арифметика. Алгоритмы. Сложность вычислений: уч. пособие/ С.Б. Гашков, В.Н. Чубариков,-2-е изд., перераб. – М.: Высшая школа 2010
12. Пантелеев, А.В. Методы оптимизации в примерах и задачах /А.В. Пантелеев, Т.А. Летева. –М.: Высшая школа, 2010
13. Режим доступа: https://www. exponenta.ru – «Образовательный математический сайт Exponenta.ru».
14. Режим доступа: https://www. matclub.ru – Лекции, примеры решения задач, интегралы и производные, дифференцирование, ТФКП, Электронные учебники. Типовой расчет из задачника Кузнецова.
15. Режим доступа: https://www. math.ru – «Образовательный математический сайт Math.ru».
16. Кострова, Ю. С. Метод проектов на занятиях по высшей математике в контексте компетентностного подхода [Текст] / Ю. С. Кострова // Молодой ученый. — 2011. — №8. — С. 114-117.
17. Самаров, К.А. Финансовая математика. Практический курс: уч. пособ./ К.А. Самаров.–М.:ИНФРА-М, 2010