Пример решения задачи
Восстановите сводную таблицу распределения данных измерения по следующей информации:
| варианта | сумма | ||||
| №1 | №2 | №3 | №4 | ||
| кратность | х | у | х + у | ||
| частота | |||||
| частота, % | 23*х - 23 | у 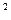 - у - 70 - у - 70
|
а) найдите х;
б) найдите у;
в) найдите моду этого распределения.
Решение.
Вспомним формулы:
ЧАСТОТА ВАРИАНТЫ= 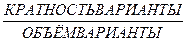
|
ЧАСТОТА ВАРИАНТЫ, В %= 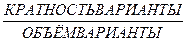 * 100% * 100%
|
В последнем столбце сумма частот всегда равна 1, а сумма частот в процентах всегда равна 100. Правильнее всего начинать восстановление информации с того столбца, в котором уже заполнено больше всего клеток – в данном случае с варианты №1 и №2. Всего было 50 результатов. Частота этой варианты равна х/50, а процентная частота в сто раз больше частоты, то есть равна 2*х. Получаем:
частота варианты, в % = (частота варианты)*100 = 23*х – 23 = 2*х.
То есть 23*х – 23 = 2*х. Решив это уравнение, получаем х = 5.
Аналогично, решаем для варианты №2:
частота варианты, в % = (частота варианты)*100 = у 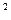 - у - 70 = 2*у.
- у - 70 = 2*у.
Решая уравнение у 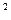 - у - 70 = 2*у, получаем: у = 10.
- у - 70 = 2*у, получаем: у = 10.
Восстанавливаем остальные неизвестные величины.
Получаем заполненную таблицу:
| варианта | сумма | ||||
| №1 | №2 | №3 | №4 | ||
| кратность | |||||
| частота | 0,4 | 0,1 | 0,2 | 0,3 | |
| частота, % |
Задача для самостоятельного решения:
1. Восстановите сводную таблицу распределения данных измерения по следующей информации:
| варианта | сумма | ||||
| №1 | №2 | №3 | №4 | ||
| кратность | 2*к | 4*к | |||
| частота | |||||
| частота, % | 3*к | к 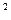 – 7*к - 33 – 7*к - 33
|
2. Изменение численности работающих на некотором предприятии характеризуется следующими данными:
| годы | численность работающих человек |
По этим данным:
а) построить сгруппированный ряд численности работающих человек;
б) определить моду, медиану, размах, среднее ряда численности работающих человек;
в) построить многоугольник распределения численности работающих человек;
г) гистограмму распределения численности работающих человек.
ВНИМАНИЕ. В предыдущей лекции ошибка. Очевидно, что сумма вероятностей противоположных событий равна единице (а не нулю).
Теория вероятностей (продолжение)
Итак, сумма вероятностей противоположных событий равна единице, то есть:
Р(А) + Р(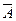 ) = 1 ) = 1
|
где Р(А) – вероятность события А, а Р(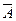 ) – вероятность противоположного ему события
) – вероятность противоположного ему события 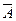 .
.
Рассмотрим пример:
Пример. Ученику предложили написать на доске любое двузначное число. Найти вероятность того, что это число:
а) не оканчивается нулём;
б) состоит из различных цифр;
в) не является квадратом целого числа;
г) не делится на 17.
Решение. Всего имеется 90 двузначных чисел (от 10 до 99), то есть в данном случае N = 90.
а) пусть А – интересующее нас событие, а 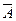 - противоположное ему событие; событие
- противоположное ему событие; событие 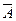 состоитв том, что число оканчивается нулём, таких чисел девять: 10, 20, 30, 40, 50, 60, 70, 80, 90; значит N(
состоитв том, что число оканчивается нулём, таких чисел девять: 10, 20, 30, 40, 50, 60, 70, 80, 90; значит N(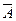 ) = 9,
) = 9,
Р(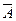 ) = N(
) = N(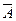 )/ N = 9/90 = 0.1 и Р(А) = 1 - Р(
)/ N = 9/90 = 0.1 и Р(А) = 1 - Р(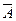 ) = 0.9.
) = 0.9.
б) пусть А – интересующее нас событие, а 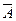 - противоположное ему событие. Оно состоит в том, что число состоит из одинаковых цифр; таких чисел ровно девять: 11, 22, 33, 44, 55, 66, 77, 88. 99; значит, N(
- противоположное ему событие. Оно состоит в том, что число состоит из одинаковых цифр; таких чисел ровно девять: 11, 22, 33, 44, 55, 66, 77, 88. 99; значит, N(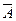 ) = 9,
) = 9,
Р(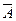 ) = N(
) = N(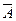 )/ N = 9/90 = 0.1 и Р(А) = 1 - Р(
)/ N = 9/90 = 0.1 и Р(А) = 1 - Р(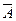 ) = 0.9.
) = 0.9.
в) следует найтиР(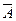 ), где событие А состоит в том, что число является квадратом целого числа; таких двузначных чисел шесть: 16, 25. 36, 49, 64, 81; значит: N(А) = 6; Р(А) = 6/90 = 1/15; Р(
), где событие А состоит в том, что число является квадратом целого числа; таких двузначных чисел шесть: 16, 25. 36, 49, 64, 81; значит: N(А) = 6; Р(А) = 6/90 = 1/15; Р(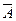 ) = 1 – Р(А) = 14/15.
) = 1 – Р(А) = 14/15.
г) следует найти Р(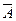 ), где событие А состоит в том, что делится на 17; таких чисел пять: 17, 34, 51, 68, 85; значит, N(А) = 5; Р(А) = 5/90 = 1/18; Р(
), где событие А состоит в том, что делится на 17; таких чисел пять: 17, 34, 51, 68, 85; значит, N(А) = 5; Р(А) = 5/90 = 1/18; Р(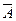 ) = 1 – Р(А) = 17/18.
) = 1 – Р(А) = 17/18.
Ответ: а) 0,9; б) 0,9; в) 14/15; г) 17/18.
Однако, существует множество задач, в которых очень непросто найти количество случаев, в которых наступает интересующее нас событие или общее количество событий при данном испытании. Часто в таких случаях применяют формулы комбинаторики.
Формулы комбинаторики
Введём определение: произведение подряд идущих первых п натуральных чисел обозначают п! и называют «эн факториал»:
Значения п! очень быстро возрастают с увеличением п:
1! = 1;
2! = 1*2 = 2;
3! = 1*2*3 = 6;
4! = 1*2*3*4 = 24;
5! = 1*2*3*4*5 = 120;
6! = 1*2*3*4*5*6 = 720;
7! = 1*  2*3*4*5*6*7 = 5040;
2*3*4*5*6*7 = 5040;
8! = 1*2*3*4*5*6*7*8 = 40320;
9! = 1*2*3*4*5*6*7*8*9 = 362880;
10! = 1*2*3*4*5*6*7*8*9*10 = 3628800.
Число перестановок из п различных элементов 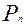


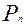 = п!. п различных элементов можно расставить по одному на п различных мест п! способами.
= п!. п различных элементов можно расставить по одному на п различных мест п! способами.
Пример. К хозяину дома пришли гости А, В, С, Д, За круглым столом – 5 разных стульев.
а) сколькими способами можно рассадить гостей за столом;
б) сколькими способами можно рассадить гостей за столом, если место хозяина уже занято;
в) сколькими способами можно рассадить гостей за столом, если гостя С следует посадить рядом с гостем А;
г) сколькими способами можно рассадить гостей за столом, если известно, что гостя А не следует сажать рядом с гостем Д.
Решение. а) на 5 стульев должны сесть 5 человек. Значит всего имеется 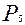 способов их рассаживания:
способов их рассаживания: 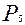 = 5! = 120;
= 5! = 120;
б) так как место хозяина фиксировано, то следует рассадить четырёх гостей на четыре места. Это можно сделать 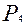 = 4! = 24 способами;
= 4! = 24 способами;
в) сначала выберем место для гостя А. Возможны 5 вариантов. если место А известно, то гостя С следует посадить или справа или слева от А, всего 2 варианта. После того как места для А и С выбраны, нужно трёх человек произвольно рассадить на 3 оставшиеся места: 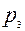 = 3! = 6. остаётся применить правило умножения: 5*2*6 = 60.
= 3! = 6. остаётся применить правило умножения: 5*2*6 = 60.
г) решение такое же, как в пункте в). Место для гостя Д после выбора места для А можно также выбрать двумя способами: на два отдалённых от А стула.
Ответ: а) 120; б) 24; в) 60; г) 60.
Число сочетан ий из п элементов по к и число размещений из п элементов по к
Число всех выборов к элементов из п данных без учёта порядка называют числом сочетаний из п элементов по к и обозначают 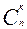 . Число всех выборов к элементов из п данных с учётом порядка называют число размещений из п элементов по к и обозначают
. Число всех выборов к элементов из п данных с учётом порядка называют число размещений из п элементов по к и обозначают 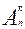 .
.
Для любых натуральных чисел п и к, таких, что к меньше п, справедливы соотношения:


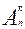 =
= 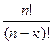

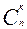 =
= 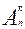 / к!
/ к!
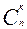 =
= 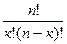
Пример. В классе 27 учеников, из них нужно выбрать троих. Сколькими способами это можно сделать, если:
а) первый ученик должен решить задачу, второй – сходить за мелом, третий – пойти дежурить в столовую;
б) им следует спеть хором.
Решение. В случае а) порядок важен, а в случае б) – нет. Значит, в первом случае получим 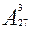 , во втором -
, во втором - 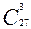 .
.
а) 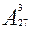 = 27*26*25 = 17550;
= 27*26*25 = 17550;
б) 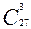 =
= 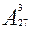 / 3! = 27*26*25/1*2*3 = 9*13*25 = 2925.
/ 3! = 27*26*25/1*2*3 = 9*13*25 = 2925.
Заключение. Изучить материалы лекции.