Занятие 2. 26.02.20.
Предельные циклы в уравнении Ван-дер-Поля
Общий вид: 
Осреднённые уравнения (общий вид)
где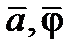 
медленно меняющиеся амплитуда и фаза.
Рассмотрим уравнение (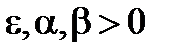
, 
– малый параметр)
Построим осредненные уравнения для переменных Ван-дер-Поля. Вычисляя интегралы, получим
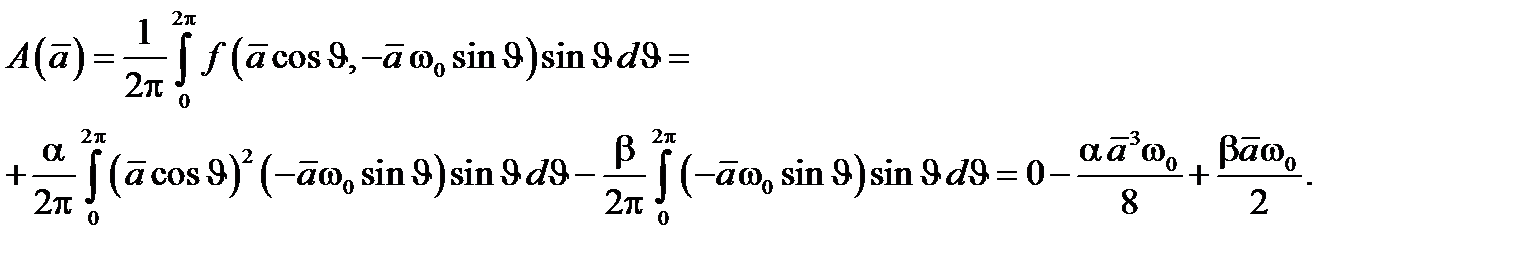
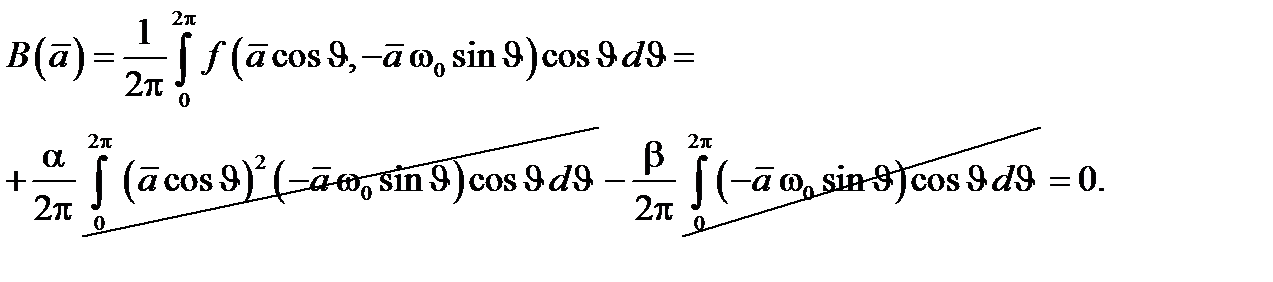
Откуда осредненные уравнения будут
То есть
Амплитуда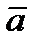 
остается постоянной (что соответствует периодическому решению), когда правая часть осредненного уравнения для амплитуды обращается в ноль, если 
Таким образом, амплитуда предельного цикла автоколебаний равна
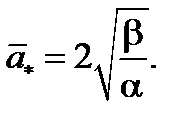
Покажем, что полученное периодическое решение устойчиво.
Действительно
и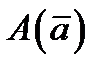 
, равная нулю при 
, является при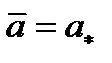 
убывающей функцией (здесь будет полезен график ).
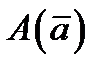Если 
и амплитуда возрастает. Если 
и амплитуда убывает, стремясь к значению 
.
Таким образом, получено, что уравнение Ван-дер-Поля 
имеет устойчивое периодическое решение
.
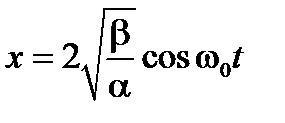Замечание.
Особенностью нелинейных систем является возможность существования изолированных периодических режимов.
Ниже приведены некоторые результаты расчётов уравнения Вани-дер-Поля с устойчивым периодическим режимом
y"+y+0.1(y^2-1)y'=0, y(0)=1,y'(0)=0
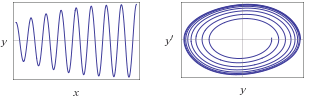
| y"+y+0.1(y^2-1)y'=0, y(0)=2.1,y'(0)=0
|
Видно, как траектория, начинаясь внутри или снаружи предельного цикла, наматывается на замкнутую кривую.
Если положить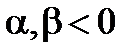 
, то получим неустойчивое периодическое решение. Результаты посмотрите на графиках
y"+y-0.1(y^2-1)y'=0, y(0)=1.99,y'(0)=0
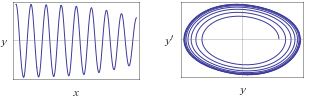
| y"+y-0.1(y^2-1)y'=0, y(0)=2.1,y'(0)=0
|
Уравнение Ван-дер-Поля с учетом кубической нелинейности консервативной силы
Рассмотрим уравнение (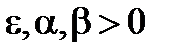, – малый параметр)
.
Осреднённые уравнения (общий вид)
Построим осредненные уравнения для переменных Ван-дер-Поля. Вычисляя интегралы, получим
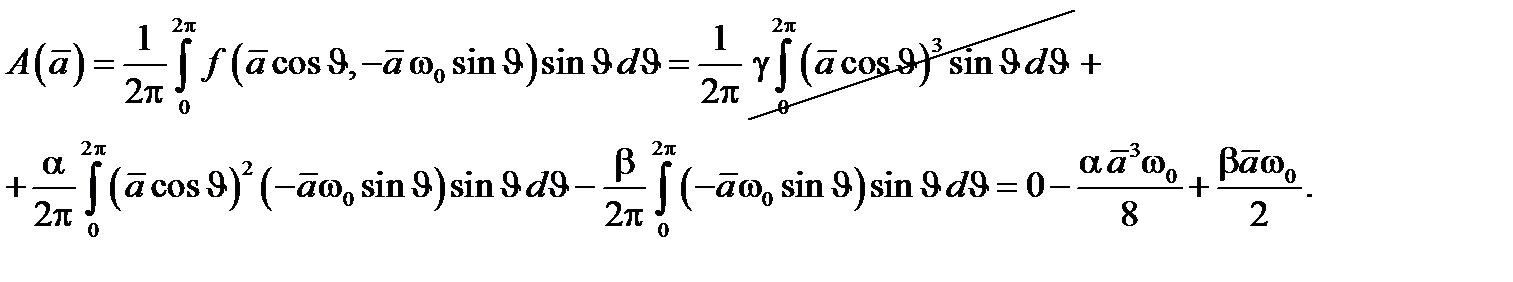
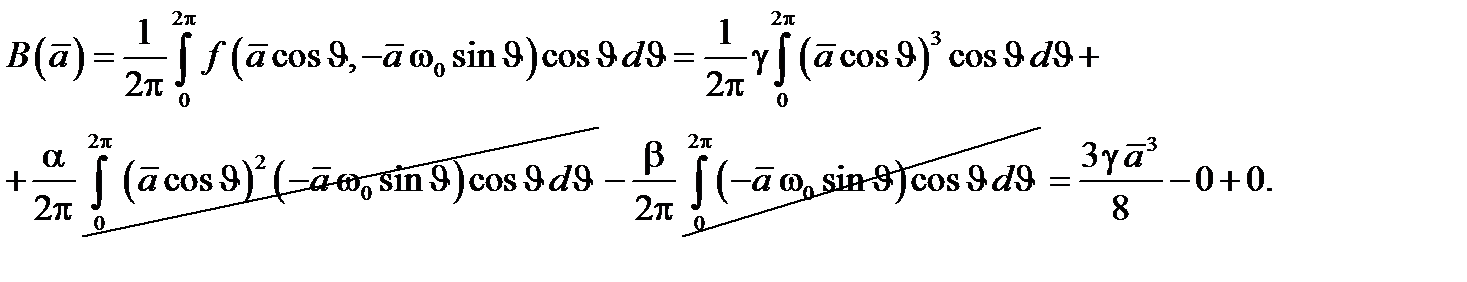
То есть
.
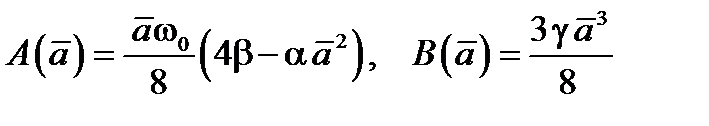Откуда осредненные уравнения будут
Правая часть осредненного уравнения для амплитуды обращается в ноль, если , то есть при
Таким образом, амплитуда предельного цикла автоколебаний равна 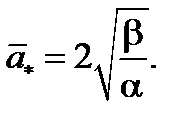Полученное периодическое решение устойчиво.
Действительно
и 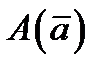является убывающей функцией. Если и амплитуда возрастает. Если и амплитуда убывает, стремясь к значению .
Частота колебаний равна
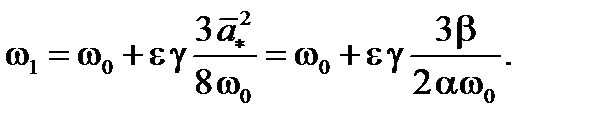
Таким образом, получено, что уравнение Ван-дер-Поля 
имеет устойчивое периодическое решение
.
Автоколебания. Случай «жесткого» возбуждения колебаний. Два периодических решения.
Рассмотрим уравнение (
, – малый параметр)
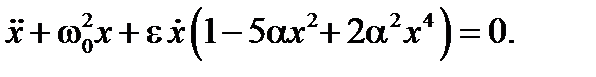
Осредненные уравнения
где
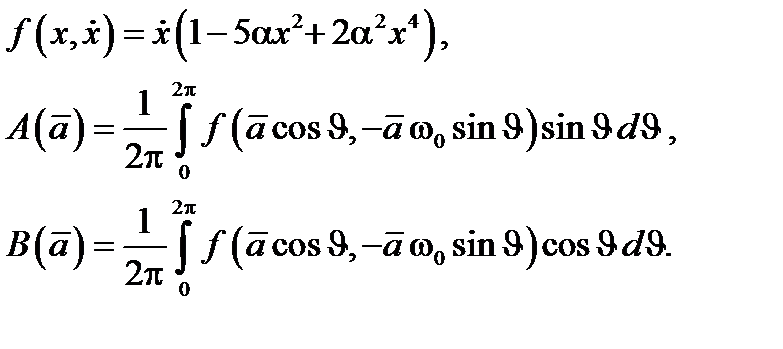
Заметим, что
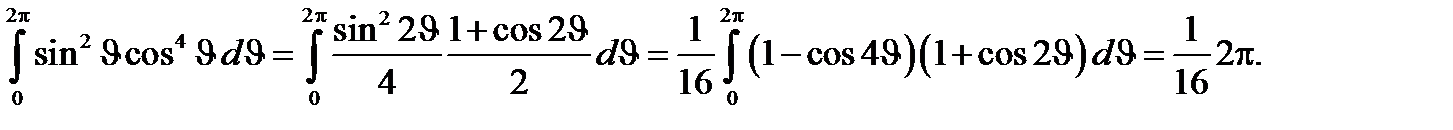
Вычисляя интегралы
Тогда
Следовательно, условию 
, соответствуют 2 значения амплитуды
Система имеет три стационарных режима, причем устойчивое состояние равновесия и устойчивый предельный цикл (аттрактор) разделены неустойчивым предельным циклом (репеллером). Все траектории, начинающиеся внутри неустойчивого предельного цикла, асимптотически приближаются к устойчивому состоянию равновесия и только траектории, начинающиеся вне неустойчивого предельного цикла, будут наматываться на устойчивый предельный цикл. Неустойчивый предельный цикл является границей, разделяющей "области притяжения" устойчивого состояния равновесия и устойчивого автоколебательного режима. Для возникновения в генераторе автоколебаний, системе необходимо сообщить толчок конечной величины.