Курс «Теория оптимального управления»
Основные экзаменационные вопросы
Понятие об оптимальном управлении в динамических системах. Вариационные задачи в форме Лагранжа, Майера, Больца. Взаимные трансформации этих задач.
Функционал для задачи максимального быстродействия.
Экстремум функции многих переменных с учетом ограничений в форме равенств. Метод множителей Лагранжа. Необходимые условия и условия максимума – минимума (через матрицу вторых производных).
Экстремум функции многих переменных. Задача без ограничений - необходимые условия экстремума. Условия максимума-минимума.
Экстремум функции многих переменных с ограничениями в форме равенств. Метод множителей Лагранжа. Условия максимума-минимума
Уравнение Эйлера для простой задачи вариационного исчисления с закрепленными концами траектории (дать вывод).
Вариационный метод решения задачи на экстремум функционала при наличии дополнительных неголономных (нет интегралов и производных) связей.
Вырожденный функционал в классической вариационной задаче. Уравнение Эйлера для вырожденного функционала.
Вариационный метод решения задачи на экстремум функционала с дополнительными связями в виде обыкновенных дифференциальных уравнений. Множители Лагранжа.
Метод динамического программирования. Функция и уравнение Беллмана для динамической системы в виде ОДУ с функционалом в форме Лагранжа.
Принцип максимума Понтрягина. Сопряженные переменные. Особенности решения задачи оптимального управления в автономном случае. Время задано или не задано.
Вариационное исчисление. Понятия вариации и функционала. Уравнение Эйлера и граничные условия для его решения. Условие минимума-максимума Лежандра.
Решение задачи максимального быстродействия с помощью принципа максимума Понтрягина. Особенности решения в стационарном (автономном) случае
Метод динамического программирования. Функция Беллмана и уравнение Беллмана для функционала в форме Лагранжа, граничное условие для этого уравнения.
Линейно-квадратичная задача оптимального управления. Синтез оптимального регулятора методом динамического программирования. Уравнение Риккакти.
Линейно-квадратичная задача оптимального управления. Синтез асимптотического оптимального регулятора методом динамического программирования (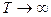
). Решение уравнения Риккати.
Граничные условия для сопряженных переменных (и множителей Лагранжа) в задачах оптимального управления, решаемых с помощью принципа максимума (или классического вариацион. исчисления). Указать, в каких случаях и как определяются.
Линейно-квадратичная задача оптимального управления в стационарном случае при неограниченном времени управления. Получение оптимального решения с гарантией требуемого запаса устойчивости.
Характерные экзаменационные примеры (2-й вопрос в билетах).
Найти точку экстремума для заданной функции нескольких переменных при наличии ограничения в форме равенства и выявить тип экстремума
Исследовать на экстремум заданную квадратичную функцию нескольких переменных при наличии линейного ограничения в форме равенства
Решить вариационную задачу (найти экстремаль и проверить на макс-мин) для функционала в виде интеграла, зависящего от производной второго порядка для искомой функции.
Решить вариационную задачу для функционала в виде интеграла, зависящего от производной первого порядка для искомой функции с учетом того, левый конец экстремали фиксирован, а правый конец оканчивается на заданной кривой.
Синтезировать асимптотически оптимальный регулятор для заданной линейной системы с квадратичным функционалом
Составить функцию и уравнение Беллмана для заданной системы управления и выявить структуру (логику) оптимального управления
Для заданной системы и функционала показать ход решения при поиске оптимального управления классическим вариационным методом. Учесть, что часть граничных условий задана, а часть – не задана.
Решить оптимизационную задачу методом динамического программирования для простой линейной системы с квадратичным функционалом.
Показать ход решения принципом максимума Понтрягина оптимизационной задачи на максимальное быстродействие для заданной системы
Решить задачу на максимальное быстродействие (принципом максимума Понтрягина) для простой линейной системы с функционалом в форме интеграла
ПРИМЕЧАНИЕ: конкретные задачи достаточно простые (системы 1-го или 2-го порядка), и могут быть решены полностью. Но в некоторых случаях достаточно только показать ход решения или выявить логику оптимального управления.