ВАРИАЦИОННЫЕ МЕТОДЫРЕШЕНИЯ КРАЕВЫХ ЗАДАЧ.
МЕТОД РИТЦА ДЛЯ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ
ИЗГИБА БАЛКИ
Решение многих краевых задач для дифф. уравнений можно свести к задаче нахождения 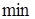 некоторого функционала
некоторого функционала 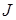 (см. лекцию 6) при соответствующих граничных условиях. При этом дифф. уравнение является уравнением Эйлера-Лагранжа для функционала
(см. лекцию 6) при соответствующих граничных условиях. При этом дифф. уравнение является уравнением Эйлера-Лагранжа для функционала 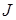 . Методы решения дифф. уравнений путем минимизации функционалов называют прямыми методами вариационного исчисления.
. Методы решения дифф. уравнений путем минимизации функционалов называют прямыми методами вариационного исчисления.
Например, функционалы 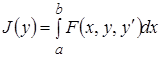 , (8)
, (8)
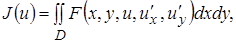 (12)
(12)
для которых уравнения Эйлера-Лагранжа имеют вид:
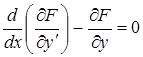 (9)
(9)
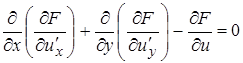 (12¢)
(12¢)
и соответствуют дифф. уравнениям 2-го порядка (обыкновенным и в частных производных) при граничных условиях:
а) 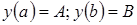 и б)
и б) 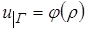 .
.
Таким образом, решение дифф. уравнения (краевой задачи) можно получить путем минимизации соответствующего функционала 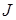 , поскольку минимизирующая функция функционала является решением соответствующего уравнения Эйлера-Лагранжа – исходного дифф. уравнения.
, поскольку минимизирующая функция функционала является решением соответствующего уравнения Эйлера-Лагранжа – исходного дифф. уравнения.
Рассмотрим два из них.
Метод Ритца
Пусть 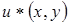 есть точное решение задачи (12) или (8) и
есть точное решение задачи (12) или (8) и 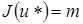 .Если удастся построить функцию
.Если удастся построить функцию 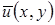 , которая удовлетворяет граничным условиям и для которой
, которая удовлетворяет граничным условиям и для которой 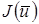 весьма близко к
весьма близко к 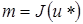 , то следует ожидать, что
, то следует ожидать, что 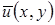 будет хорошим приближением к истинному решению задачи. Если же удастся построить минимизирующую последовательность
будет хорошим приближением к истинному решению задачи. Если же удастся построить минимизирующую последовательность 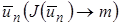 , то есть основание ожидать, что такая последовательность
, то есть основание ожидать, что такая последовательность 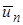 будет в том или ином смысле сходиться к решению.
будет в том или ином смысле сходиться к решению.
Для физического нахождения функции 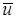 , дающей значение
, дающей значение 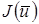 , близкое к минимальному, Ритцем был предложен следующий метод (1908 г.).
, близкое к минимальному, Ритцем был предложен следующий метод (1908 г.).
Рассматривается семейство функций, зависящее от нескольких параметров и удовлетворяющее граничным условиям краевой задачи:
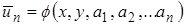 (1)
(1)
Найдем среди допустимых функций ту, которая дает функционалу 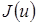 наименьшее значение. Эта задача является уже несравненно более легкой, чем первоначальная. Действительно, подставив в функционал
наименьшее значение. Эта задача является уже несравненно более легкой, чем первоначальная. Действительно, подставив в функционал 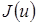 вместо
вместо 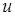 выражение
выражение 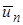 (1) и выполнив необходимые операции дифференцирования и интегрирования, получим функцию
(1) и выполнив необходимые операции дифференцирования и интегрирования, получим функцию 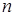 переменных
переменных 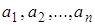 , т.е.
, т.е. 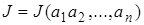 . Так как мы должны добиться
. Так как мы должны добиться 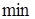 этой функции, то числа
этой функции, то числа 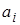 должны удовлетворять системе уравнений
должны удовлетворять системе уравнений
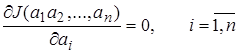 (2)
(2)
Решив эту систему, получим определенные значения параметров 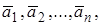 дающие функции
дающие функции 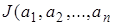 ) абсолютный минимум. В результате среди функций (1), выбрав функцию, отвечающую именно этим значениям параметров, получим требуемое приближенное решение
) абсолютный минимум. В результате среди функций (1), выбрав функцию, отвечающую именно этим значениям параметров, получим требуемое приближенное решение
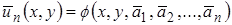 (3)
(3)
Наиболее практически важных случаях в интеграле 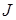 подинтегральное выражение представляет собой многочлен второй степени относительно
подинтегральное выражение представляет собой многочлен второй степени относительно 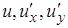 . Если семейство (1) берется линейно зависящим от параметров
. Если семейство (1) берется линейно зависящим от параметров 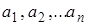 :
:
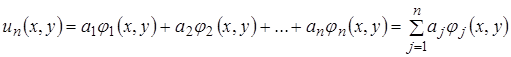 , (4)
, (4)
то квадратичный функционал 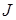 будет квадратичной функцией параметров
будет квадратичной функцией параметров 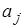 . Поэтому задача нахождения минимума квадратичной функции
. Поэтому задача нахождения минимума квадратичной функции 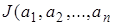 ) посредством дифференцирования (2) по
) посредством дифференцирования (2) по 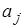 сводится к системе минимальных алгебраических уравнений. Система линейных алгебраических уравнений нетрудно решается при
сводится к системе минимальных алгебраических уравнений. Система линейных алгебраических уравнений нетрудно решается при 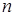 ~ 102. Практически бывает достаточным
~ 102. Практически бывает достаточным 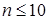 .
.
Примеры. 1) Пусть имеется 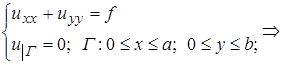
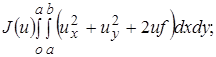
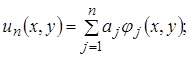
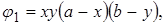
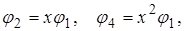
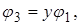
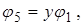
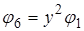 и т.д.
и т.д.
Тогда 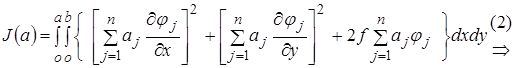
 .
.
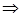 Систему уравнений
Систему уравнений 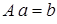 , где
, где 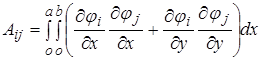
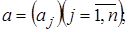
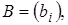
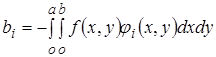 ;
; 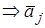 .
.
 2)
2) 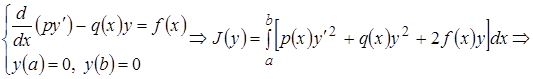

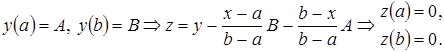
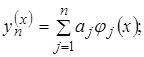
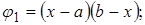
 . Тогда
. Тогда
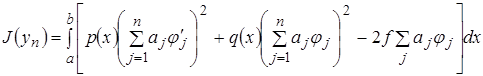 .
.
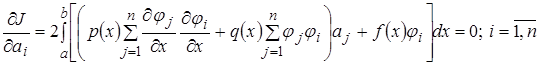
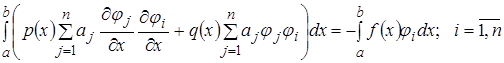
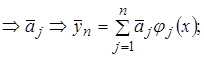
Остановимся теперь на вопросе о том, в каком случае методом Ритца можно получить сколь угодно близкое приближение к действительному 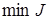 . Получаем
. Получаем 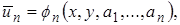
 причем
причем 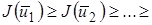 . Когда последовательность
. Когда последовательность 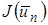 стремится к истинному минимуму:
стремится к истинному минимуму:
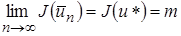 (5)
(5)
Достаточным условием для этого является полнота системы семейств (1), которая состоит в следующем: каковы бы ни были функция 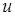 непрерывна вместе с
непрерывна вместе с 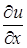 и
и 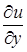 и удовлетворяющая граничному условию
и удовлетворяющая граничному условию 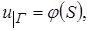 и
и 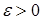 , можно будет указать такое
, можно будет указать такое 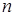 и такую функцию среди
и такую функцию среди  семейства (1):
семейства (1):  , что повсюду в области D будут справедливы неравенства:
, что повсюду в области D будут справедливы неравенства:
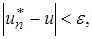
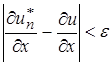 ,
, 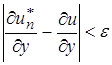 , т.е. любая функция может быть сколь угодно аппроксимирована вместе с частными производными посредством функций из семейств (1). Полноту системы обычно удается обнаруживать, пользуясь обобщенной теоремой Вейерштрасса:
, т.е. любая функция может быть сколь угодно аппроксимирована вместе с частными производными посредством функций из семейств (1). Полноту системы обычно удается обнаруживать, пользуясь обобщенной теоремой Вейерштрасса:
Т. Если для 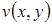 непрерывна в замкнутой ограниченной области D вместе с частными производными
непрерывна в замкнутой ограниченной области D вместе с частными производными 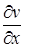 и
и 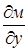 , то можно по
, то можно по 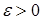 указать такой полином
указать такой полином 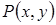 , что в области будут выполнены неравенства:
, что в области будут выполнены неравенства:
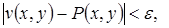
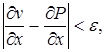
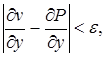 (6)
(6)
С помощью этой теоремы можно установить полноту исследующей системы функций: пусть 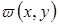 - непрерывная и имеющая внутри D ограниченные и непрерывные производные
- непрерывная и имеющая внутри D ограниченные и непрерывные производные 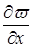 и
и 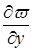 ; и
; и 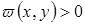 внутри D и
внутри D и 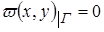 . Тогда в качестве основной системы функций (1) можно принять:
. Тогда в качестве основной системы функций (1) можно принять:
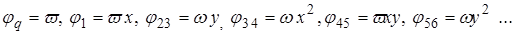 (7)
(7)
Функции 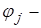 называются базисными (координатными функциями).
называются базисными (координатными функциями).
Для прямоугольника [ 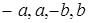 ]
] 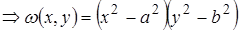
Если уравнение границы Г: 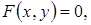 где F - непрерывна вместе с частными производными, то
где F - непрерывна вместе с частными производными, то 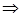
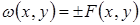 . Иногда берут комбинации тригонометрических функций. Замечание. Пусть имеется операторное уравнение АУ =
. Иногда берут комбинации тригонометрических функций. Замечание. Пусть имеется операторное уравнение АУ = 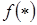 . Если А положительно определенный
. Если А положительно определенный 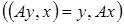 и
и 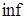
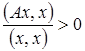 или
или 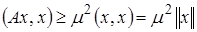 -самосопряженный оператор (линейный оператор, совпадающий со своим сопряженным оператором А=А*®
-самосопряженный оператор (линейный оператор, совпадающий со своим сопряженным оператором А=А*® 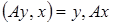 аналогично симметрии матриц, то метод Ритца позволяет получить решение уравнения (*)
аналогично симметрии матриц, то метод Ритца позволяет получить решение уравнения (*)
Метод Бубнова-Галеркина (1915 г.)