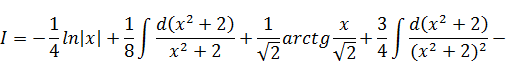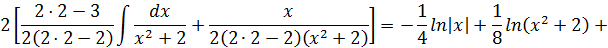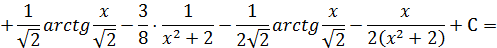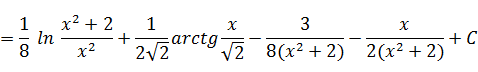Итак,
При вычислении интегралов вида
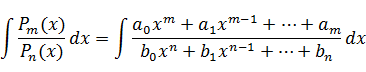
если степень числителя выше или равна степени знаменателя, т.е. т 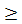 п, многочлен в числителе делят на многочлен, стоящий в знаменателе, и таким образом представляют данную дробь в виде суммы многочлена и некоторой правильной рациональной дроби, т.е. дроби, степень числителя которой ниже степени знаменателя, а именно, в виде
п, многочлен в числителе делят на многочлен, стоящий в знаменателе, и таким образом представляют данную дробь в виде суммы многочлена и некоторой правильной рациональной дроби, т.е. дроби, степень числителя которой ниже степени знаменателя, а именно, в виде
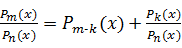
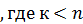 .
.
Интеграл от многочлена 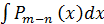 вычисляется легко и, следовательно, вся задача сводится к вычислению второго интеграла
вычисляется легко и, следовательно, вся задача сводится к вычислению второго интеграла 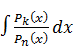 .
.
Рассмотрим различные случаи интегрирования рациональных дробей.
I. Многочлен знаменателя 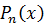 имеет различные действительные корни кратности единица. Т.е. разложение многочлена
имеет различные действительные корни кратности единица. Т.е. разложение многочлена 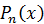 на множители имеет вид:
на множители имеет вид:
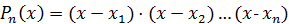 .
.
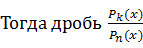 разлагается на простейшие дроби такого типа
разлагается на простейшие дроби такого типа
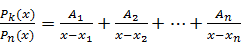 .
.
Далее справа в полученном разложении дроби приводятся к общему знаменателю, после этого приравниваются числители обеих дробей справа и слева.
Коэффициенты А1, А2,..., Ап можно найти двумя способами:
1) т.к. многочлены равны, когда равны коэффициенты при одинаковыхстепенях х, то после раскрытия скобок в правом числителе приравнивают коэффициенты справа и слева и таким образом получают систему п линейных уравнений с n неизвестными;
2) более простой способ: подставлять в полученное равенство последовательно вместо х значения корней х1, х2,..., хп.
Примеры:
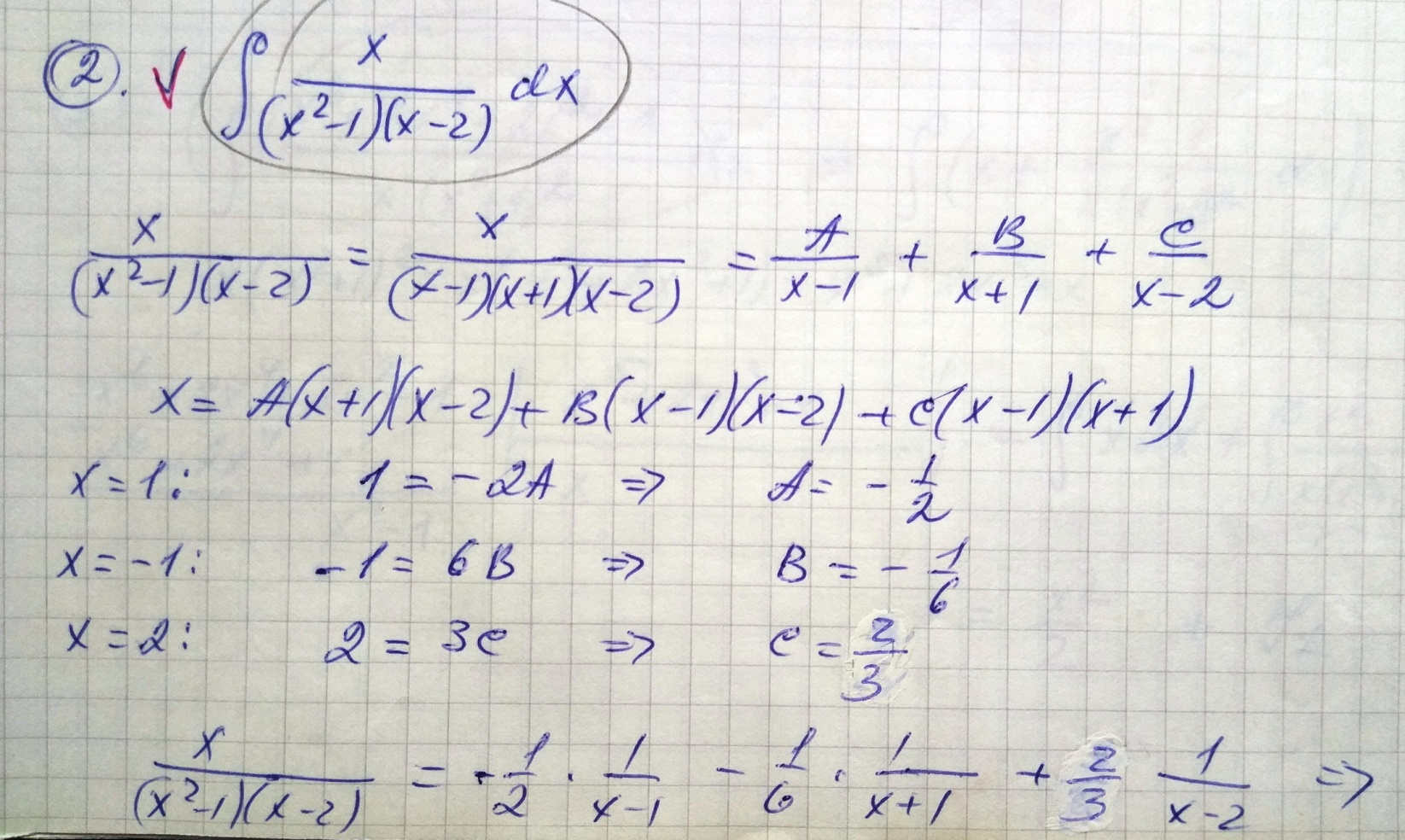
| 1. | 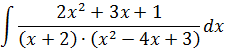 Подынтегральную функцию представим в виде суммы простейших дробей, разложив в знаменателе трехчлен на множители:
Подынтегральную функцию представим в виде суммы простейших дробей, разложив в знаменателе трехчлен на множители:
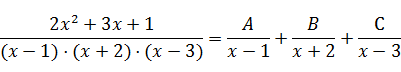 После приведения справа дробей к общему знаменателю и приравнивания числителей получаем тождество:
После приведения справа дробей к общему знаменателю и приравнивания числителей получаем тождество:
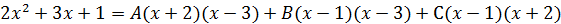 При
При 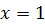 получаем получаем 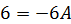 , откуда , откуда 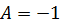 .
При .
При 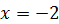 получаем получаем 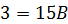 , откуда , откуда 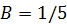 .
При .
При 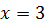 получаем получаем 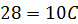 , откуда , откуда 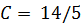 .
Тогда .
Тогда
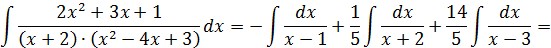
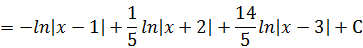
|
| 2. | 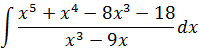 Степень многочлена в числителе больше степени многочлена в знаменателе, поэтому разделим числитель на знаменатель:
Степень многочлена в числителе больше степени многочлена в знаменателе, поэтому разделим числитель на знаменатель:
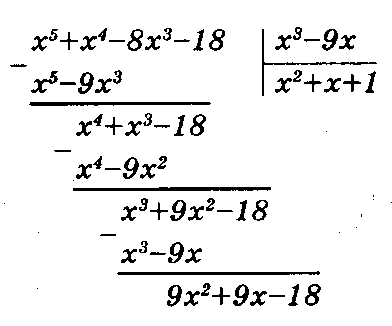 Тогда подынтегральная дробь запишется в виде
Тогда подынтегральная дробь запишется в виде
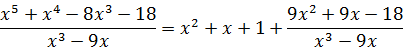 Разложим
Разложим 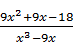 на простейшие дроби на простейшие дроби
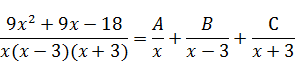 Отсюда следует тождество
Отсюда следует тождество
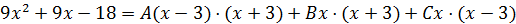 При
При 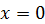 получаем получаем 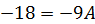 , откуда , откуда 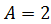 .
При .
При 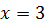 получаем получаем 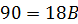 , откуда , откуда 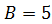 .
При .
При 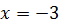 получаем получаем 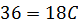 , откуда , откуда 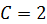 .
Таким образом .
Таким образом
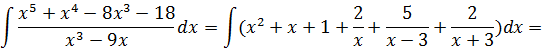
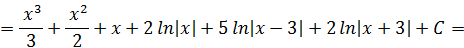
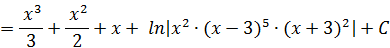
|
II. Пусть корни 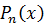 — действительные, некоторые из них кратные. Т.е. разложение многочлена на множители имеет вид:
— действительные, некоторые из них кратные. Т.е. разложение многочлена на множители имеет вид:
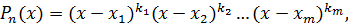 где
где 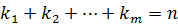
И тогда
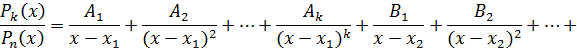
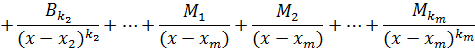
Коэффициенты 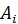 ,
, 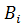 ,...,
,..., 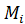 находятся такими же способами, что и в первом (I) случае. При применении второго (II) способа кроме значения корней многочлена
находятся такими же способами, что и в первом (I) случае. При применении второго (II) способа кроме значения корней многочлена 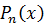 переменной х даются и другие произвольные значения.
переменной х даются и другие произвольные значения.
Пример:
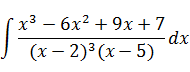 Подынтегральную функцию представим в виде суммы простейших дробей, разложив в знаменатель на множители:
Подынтегральную функцию представим в виде суммы простейших дробей, разложив в знаменатель на множители:
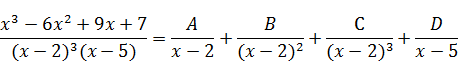 После приведения справа дробей к общему знаменателю и приравнивания числителей получаем тождество:
После приведения справа дробей к общему знаменателю и приравнивания числителей получаем тождество:
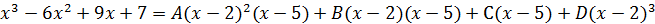 Подставим в обе части тождества последовательно корни
Подставим в обе части тождества последовательно корни 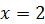 , , 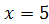 и дополнительные и дополнительные 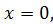 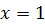 :
При :
При 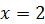 получаем получаем 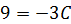 , откуда , откуда 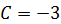 .
При .
При 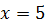 получаем получаем 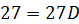 , откуда , откуда 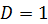 .
При .
При 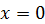 получаем получаем 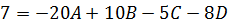 При
При 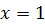 получаем получаем 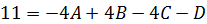 После подстановки в последние два уравнений значений С и D получим систему:
После подстановки в последние два уравнений значений С и D получим систему:
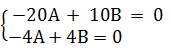 решение которой
решение которой 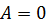 и и 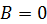 .
Таким образом, окончательно имеем: .
Таким образом, окончательно имеем:
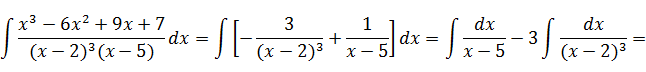
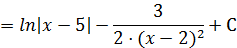
|
III. Пусть разложение многочлена 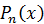 имеет вид:
имеет вид:
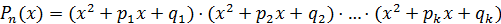 ,
,
где все трехчлены 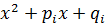 имеют дискриминант
имеют дискриминант 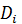 < 0 (т. е. не разлагаются на линейные множители в действительной области и имеют комплексные корни).
< 0 (т. е. не разлагаются на линейные множители в действительной области и имеют комплексные корни).
Тогда
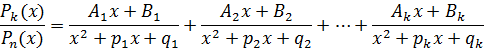
В этом случае обычно приравнивают коэффициенты при одинаковых степенях х в числителях дробей справа и слева после приведения в правой части к общему знаменателю.
Пример.
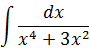 Запишем разложение для подынтегральной функций:
Запишем разложение для подынтегральной функций:
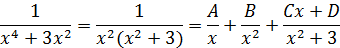 После приведения справа дробей к общему знаменателю и приравнивания числителей получаем тождество:
После приведения справа дробей к общему знаменателю и приравнивания числителей получаем тождество:
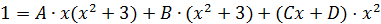 Раскроем скобки в правой части и перегруппируем:
Раскроем скобки в правой части и перегруппируем:
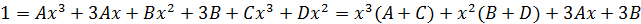 Приравниваем коэффициенты при одинаковых степенях х справа и слева.
Приравниваем коэффициенты при одинаковых степенях х справа и слева.
Таким образом, заданный интеграл принимает вид:
|
IV. Пусть корни многочлена 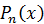 комплексные, кратные, т.е. в его разложении присутствуют скобки вида (
комплексные, кратные, т.е. в его разложении присутствуют скобки вида ( 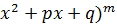 .
.
Тогда для каждой такой скобки разложение на простейшие дроби, будет иметь вид:
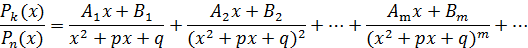
Неопределенные коэффициенты 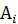 ,
, 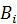 находятся способом, изложенным в предыдущих разделах.
находятся способом, изложенным в предыдущих разделах.
При этом особое внимание надо обратить на вычисление интегралов типа
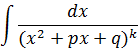
В трехчлене обычно выделяется полный квадрат:
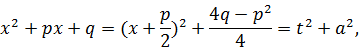
где 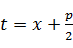 ;
; 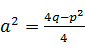 и тогда интеграл принимает вид
и тогда интеграл принимает вид
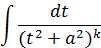
Этот интеграл вычисляется обычно по рекуррентной формуле. Выведем ее, применяя интегрирование по частям:
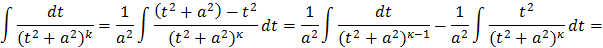
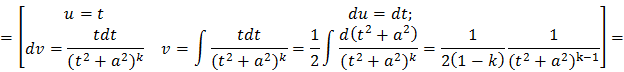
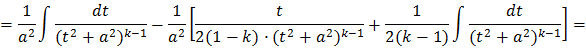
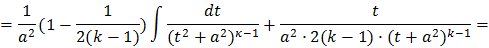
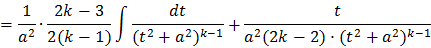
И следовательно получаем формулу:
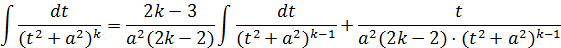
Пример:



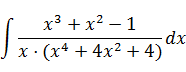 Разложим подынтегральную функцию на простейшие дроби:
Разложим подынтегральную функцию на простейшие дроби:
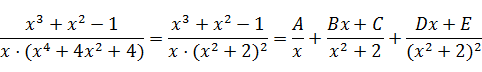 После приведения справа дробей к общему знаменателю и приравнивания числителей получаем тождество:
После приведения справа дробей к общему знаменателю и приравнивания числителей получаем тождество:
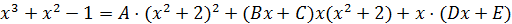 Раскроем скобки в правой части и перегруппируем:
Раскроем скобки в правой части и перегруппируем:
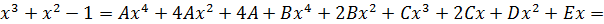
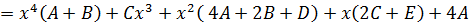 Приравниваем коэффициенты при одинаковых степенях х справа и слева, получаем систему для определения коэффициентов:
Приравниваем коэффициенты при одинаковых степенях х справа и слева, получаем систему для определения коэффициентов:
Таким образом, заданный интеграл принимает вид:
К последнему интегралу применим выведенную рекуррентную формулу для
|
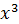 :
:
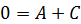
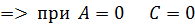
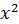 :
:
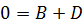
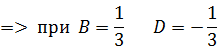
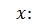
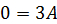
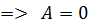
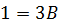
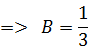
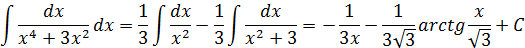
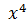 :
:
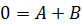
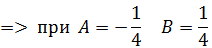
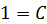
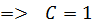
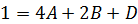
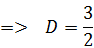
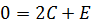
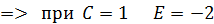
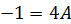
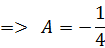
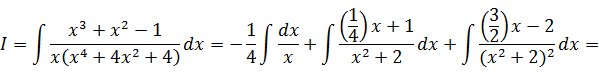
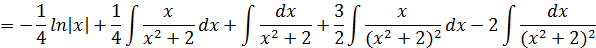
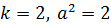 :
: