Лабораторная работа №8.
Ряды
Цель работы: разложение периодических функций в тригонометрический ряд в программе MathCad с использованием символьных операций.
Указания к выполнению лабораторной работы:
Запустить программу MathCad.
1. Исследовать ряд на сходимость
2. Найти область сходимости степенного ряда
3. Разложить функцию f(x) в ряд Фурье
ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫФУРЬЕ
При изучении разнообразных периодических процессов, т.е. процессов, которые через определённый промежуток времени повторяется (встречаются в радиотехнике, электронике, теории упругости, теории и практике автоматического регулирования и т.д.), целесообразнее разлагать периодические функции, описывающие эти процессы, не в степенной ряд, а в так называемый тригонометрический ряд.
Важным классом функциональных рядов являются тригонометрические ряды. Эти ряды удобны для разложения периодических функций, описывающих различные периодические процессы (например, переменный ток и показатели качества электрической энергии).
Тригонометрический ряд, это ряд вида

 ,
,
где a0, an bn - коэффициенты ряда (действительные числа).
Если f (x) - периодическая функция с периодом 2 p и удовлетворяет на отрезке [- p;p ] некоторым условиям (условиям Дирихле), тогда эту функцию можно разложить в тригонометрический ряд:

который называется рядом Фурье.
Коэффициенты такого ряда называются коэффициентами Фурье и вычисляются по формулам:
 ,
,  ,
,  ,
, 
Таким образом, разложение периодической функции в тригонометрический ряд Фурье сводится к вычислению определённых интегралов и записи функциональной зависимости функции.
Рассмотрим пример.
Разложим элементарную степенную функцию f(x) = x интервале [-p; p]. Все вычисления будем производить в системе Mathcad и параллельно давать комментарии к вычислениям.


Рис. 8.1 - Построение графика разлагаемой функции.
Обозначение её периода разложения.
В данном примере мы построили график функции на том интервале, на котором в дальнейшем будет происходить разложение. Этот период может быть выбран произвольно. Границы периода в данном случае задаются переменными x1 и x2.
После того, как были заданы границы периода разложения, и была задана сама функция, которая будет раскладываться на этом периоде, необходимо вычислить коэффициенты ряды Фурье – т.е. найти три определённых интеграла, а именно
 ,
,  ,
,  ,
, 
Найдём значения этих определённых интегралов.

Рис. 8.2 - Нахождение коэффициентов ряда Фурье.
После того, как были найдены коэффициенты Фурье, в зависимости от точности конечного результата задаётся число n - т.е. количество составляющих конечной функции – т.е. количество слагаемых.
Для наглядности конечных результатов построим серию графиков при разных значениях n, а также будем находить определённый интеграл на произвольном промежутке и отслеживать, как будет меняться результат.

Рис. 8.3 - Визуализация графиков для разных значений «n».
В данном примере функции были заданы одна от другой, так как при возрастании n их значения повторяются. В конечном результате они имеют следующий вид.

Рис. 8.4 - Значения функций ряда Фурье при различных значениях «n».
Данный способ задания результирующей функции является достаточно громоздким и неудобным. Однако его основное преимущество в том, что максимально нагляден.

Рис. 8.5 - Разложение функции в тригонометрический ряд Фурье «n=5».

Рис. 8.6 - Разложение функции в тригонометрический ряд Фурье «n=15».
В системе Mathcad существует возможность задания функции непосредственно через оператор Суммирование, который находится на панели Исчисление. Приведём три примера на применение этого оператора, а также отследим, как меняется точность полученного графика в сравнении с оригинальным, и найдём эту точность (смотрите выше).

Рис. 8.7 - Разложение функции в тригонометрический ряд Фурье «n=25».
Функция f (x)= x является симметричной функцией относительно начала координат, поэтому определённые интегралы
 ,
,  были равны нулю.
были равны нулю.
Рассмотрим функцию общего вида f(x) = ex и разложим её в тригонометрический ряд Фурье при помощи системы Mathcad. Пример разложения дан ниже

Рис. 8.8 - Разложение в тригонометрический ряд Фурье функции 
Для получения более точного результата зададим количество разложений nx= 45. Однако следует помнить, что время, затрачиваемое на разложение с увеличением nx, возрастает в геометрической прогрессии. Могут встречаться такие случаи, что система Mathcad может отказаться считать этот пример.

Рис. 8.9 - Разложение в тригонометрический ряд Фурье функции  «n=45».
«n=45».
ЧИСЛОВЫЕ РЯДЫ
Познакомимся с числовыми рядами, а также возможностями системы Mathcad по их исследованию. Следует отметить, что каких-либо специальных функций для исследования сходимости числовых рядов в системе Mathcad не предусмотрено, как в принципе и для тригонометрических рядов Фурье. Однако существует достаточное количество операторов, которые, при должном применении, могут оказать помощь при исследовании числовых рядов.
Сумма членов бесконечной числовой последовательности  называется числовым рядом
называется числовым рядом
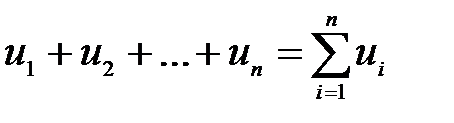 .
.
При этом числа  будем называть членами ряда, а
будем называть членами ряда, а  – общим членом ряда.
– общим членом ряда.
Суммы  , n =1, 2,…
, n =1, 2,…
называются частичными суммами ряда
Таким образом, можно рассматривать последовательности частичных сумм ряда S1, S2,…,Sn.
Ряд

называется сходящимся, если сходится последовательность его частичных сумм. Сумма сходящегося ряда – предел последовательности его частичных сумм.
 ,
, 
Если последовательность частичных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся, и суммы не имеет.
Примеры:
1) Ряд 0 + 0 + 0 + … + 0 + … очевидно сходится и его сумма равна 0.
2) Ряд 1 + 1 + 1 + …+ 1 +… расходится, т. к. его частичные
суммы  .
.
3) Ряд 1 – 1 + 1 – 1 +…+ 1 -… расходится, т. к. последовательность его частичных сумм имеет вид 1, 0, 1, 0,… и предела не имеет.
4) Ряд

представляет собой сумму бесконечно убывающей геометрической прогрессии. Этот ряд сходится и его сумма равна 2.
Рассмотрим некоторые свойства рядов.
1) Сходимость или расходимости ряда не нарушится, если изменить, отбросить или добавить конечное число членов ряда.
2) Если ряд  сходится и его сумма равна S, то ряд
сходится и его сумма равна S, то ряд 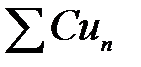 (С – постоянное число) тоже сходится, и его сумма равна СS
(С – постоянное число) тоже сходится, и его сумма равна СS
3) Рассмотрим два ряда  и
и  . Суммой или разностью этих рядов будет называться ряд
. Суммой или разностью этих рядов будет называться ряд  , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
Если ряды  и
и  сходятся и их суммы равны соответственно S и s, то ряд
сходятся и их суммы равны соответственно S и s, то ряд  тоже сходится и его сумма равна S + s.
тоже сходится и его сумма равна S + s.
 =
=  +
+  = S + s
= S + s
Далее рассмотрим необходимо условие сходимости рядов.
Если ряд  сходится, то необходимо, чтобы общий член
сходится, то необходимо, чтобы общий член  стремился к нулю. Однако это условие не является достаточным. Можно говорить только о том, что если общий член не стремится к нулю, то ряд точно расходится. Например, гармонический ряд
стремился к нулю. Однако это условие не является достаточным. Можно говорить только о том, что если общий член не стремится к нулю, то ряд точно расходится. Например, гармонический ряд

является расходящимся, хотя его общий член и стремится к нулю.
Пример: Исследовать сходимость ряда

Исследуем общий член ряда: найдём

Необходимый признак сходимости не выполняется, значит, ряд расходится.
Теперь посмотрим, как данный пример можно решить в системе Mathcad, используя при этом уже известные инструменты.

Рис. 8.10 - Исследование сходимости ряда по необходимому условию сходимости ряда.
Далее мы опишем ещё несколько признаков сходимости ряда, однако данный пример был рассмотрен потому, что, если этот признак сходимости ряда не выполняется, то нет необходимости исследовать ряд на оставшиеся признаки сходимости ряда.
Таким образом, проверка необходимого условия сходимости ряда сходится в системе Mathcad просто к вычислению предела заданной функции на бесконечности. Рассмотрим признаки сходимости рядов с неотрицательными членами.
Признак сравнения. Пусть даны два ряда  и
и 
Если 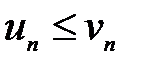 при любом n, то из сходимости ряда
при любом n, то из сходимости ряда  следует сходимость ряда
следует сходимость ряда  , а из расходимости ряда
, а из расходимости ряда  следует расходимость ряда
следует расходимость ряда  .
.
Примеры: 1) Исследовать на сходимость ряд
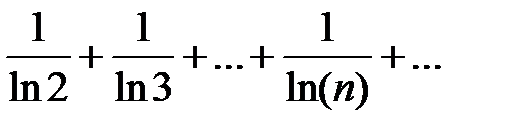
Так как  а гармонический ряд
а гармонический ряд 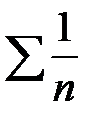 расходится, то расходится и ряд
расходится, то расходится и ряд  . Решим данный пример в системе Mathcad. Смотрите рисунок ниже.
. Решим данный пример в системе Mathcad. Смотрите рисунок ниже.

Рис. 8.11 - Исследование сходимости ряда по признаку сравнения
В данном примере мы получили, что для числового ряда  выполняется необходимое условие сходимости ряда, т.е. предел
выполняется необходимое условие сходимости ряда, т.е. предел  стремится к нулю. Далее по признаку сравнения мы получили, что на всей области значений оси Ox числовой ряд
стремится к нулю. Далее по признаку сравнения мы получили, что на всей области значений оси Ox числовой ряд  больше, чем числовой ряд
больше, чем числовой ряд 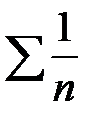 - это видно из графика функции. Пунктирная кривая отображает числовой ряд
- это видно из графика функции. Пунктирная кривая отображает числовой ряд  , a сплошная кривая отображает ряд
, a сплошная кривая отображает ряд 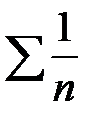 .
.
Рассмотрим другой пример.
Исследовать на сходимость ряд 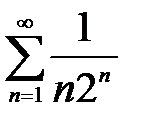
Так как  , а ряд
, а ряд  сходится (как убывающая геометрическая прогрессия), то ряд
сходится (как убывающая геометрическая прогрессия), то ряд 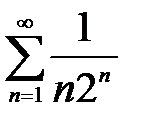 тоже сходится. Решим данный пример в системе Mathcad.
тоже сходится. Решим данный пример в системе Mathcad.

Рис. 8.12 - Исследование сходимости ряда по признаку сравнения.
Ряд  по определению является сходящимся. Из графика функции видно, что на всей области значений оси Ox числовой ряд
по определению является сходящимся. Из графика функции видно, что на всей области значений оси Ox числовой ряд  находится выше, чем числовой ряд
находится выше, чем числовой ряд 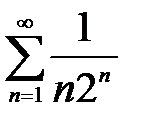 , поэтому данный ряд является сходящимся.
, поэтому данный ряд является сходящимся.
В признаке сравнения для того, чтобы исследовать сходимость или расходимость ряда, необходимо иметь «эталонный» числовой ряд, с которым можно дальше проводить сравнение.
Рассмотрим следующий признак – признак Даламбера.
Пусть дан ряд  и существует предел
и существует предел  . Тогда, если l <1, то ряд сходится, а если l >1, то ряд расходится.
. Тогда, если l <1, то ряд сходится, а если l >1, то ряд расходится.
При l = 1 ряд может как сходиться, так и расходиться, и необходимо применять другие признаки сходимости – расходимости числовых рядов.
Пример. Исследовать на сходимость ряд
 ,
, 
Вычисляем соотношение
 .
.
Следовательно, по признаку Даламбера, ряд сходится.
В системе Mathcad этот пример может быть решён следующим способом.
Примечание к примеру:
Следует обратить внимание на некоторые особенности задания функции. Как показано ниже, для того, чтобы увеличить или уменьшить переменную функции на какую-либо величину, нет необходимости задавать новую функцию и исправлять данную переменную. Достаточно в самой функции добавить изменение и вывести результат при помощи символьного вычисления.
Также важен график функции Факториала. Оператор факториала находится на панели Калькулятор.

Рис. 8.13 - Исследование сходимости ряда по признаку Даламбера.
Рассмотрим следующий пример, который показывает иллюстрацию признака Даламбера для исследования сходимости числовых рядов
 .
.
Вычисляем соотношение

Следовательно, по признаку Даламбера, ряд расходится. В системе Mathcad этот пример может быть решён следующим способом.
Также всегда рекомендуется строить графики для визуализации полученных результатов.

Рис. 8.14 - Исследование сходимости ряда по признаку Даламбера.
Под геометрическим смыслом предела подразумевается отношение последующего члена числового ряда к предыдущему – т.е. в данном случае оно равно «2». Другими словами, каждый последующий член больше предыдущего в два раза, – что указывает на то, что числовой ряд не может быть сходящимся.
Рассмотрим признак Коши.
Пусть дан ряд  и существует предел
и существует предел  . Тогда, если l <1, то ряд сходится, а если l >1, то ряд расходится.
. Тогда, если l <1, то ряд сходится, а если l >1, то ряд расходится.
При l = 1 ряд может как сходиться, так и расходиться.
Пример. Исследовать сходимость ряда
 .
.
Вычисляем предел

Следовательно, по признаку Коши, ряд сходится.
Решим этот пример в системе Mathcad.

Рис. 8.15 - Исследование сходимости ряда по признаку Коши.
Рассмотрим ещё один важный признак, который необходим для исследования сходимости рядов – это интегральный признак.
Допустим, есть ряд  и функция f(x) связанная с членами ряда f(n)=un. Тогда, если сходится несобственный интеграл
и функция f(x) связанная с членами ряда f(n)=un. Тогда, если сходится несобственный интеграл  , то сходится и ряд. Если интеграл расходящийся, то расходится и ряд.
, то сходится и ряд. Если интеграл расходящийся, то расходится и ряд.
Интегральный признак позволяет доказать расходимость гармонического ряда  . Этому ряду соответствует функция
. Этому ряду соответствует функция  . Соответствующий ей несобственный интеграл
. Соответствующий ей несобственный интеграл  расходится, т. к.
расходится, т. к.

Рассмотрим пример.
Исследовать сходимость ряда 
Этому ряду соответствует интеграл  ,
,

интеграл сходится, а значит, ряд тоже сходится.
Вообще, ряды вида  сходятся при p >1 и расходятся при p ≤ 1.
сходятся при p >1 и расходятся при p ≤ 1.
Таким образом, решение примера на определение сходимости числового ряда сводится к вычислению несобственного интеграла первого рода.
Данный пример может быть решён в системе Mathcad следующим образом.
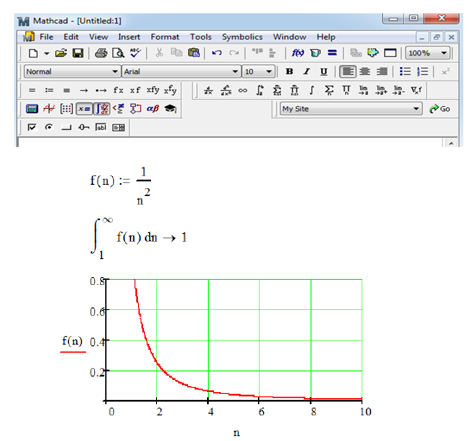
Рис. 8.16 - Исследование сходимости ряда по интегральному признаку.
Рассмотрим функциональные и степенные ряды.
Если членами ряда будут не числа, а функции, то ряд называется функциональным.

Подставляя вместо х определённое значение хо, получаем числовой ряд:

Этот ряд может быть, как сходящимся, так и расходящимся.
Исследование на сходимость функциональных рядов сложнее исследования числовых рядов. Один и тот же функциональный ряд может при одних значениях х сходиться, а при других – расходиться. Поэтому вопрос сходимости функциональных рядов сводится к определению тех значений переменной х, при которых ряд сходится. Если ряд сходится при x= x0, то точка x0 называется точкой сходимости функционального ряда. Совокупность всех точек сходимости называется областью сходимости.
Среди функциональных рядов особую роль играют степенные ряды, к оторые используются для приближенного вычисленияфункций (ряды Тейлора и Маклорена) и интегралов, решения дифференциальных уравнений и др. Степенным рядом называетсяфункциональный ряд вида
 ,
,
где a 0, a 1, a 2,…- действительные числа, коэффициенты степенного ряда.
Рассматриваются также ряды по степеням при (x-x 0)
 ,
,
где x0 - некоторое число.
Вопрос о сходимости степенных рядов очень важен. Область сходимости степенного ряда обладает некоторыми замечательными свойствами.
Для каждого степенного ряда существует такое положительное число R, что при всех x таких, что  ряд абсолютно сходится, а при всех
ряд абсолютно сходится, а при всех  ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости. Для решения вопросов о сходимости на границах интервала необходимо проводить дополнительные исследования степенного ряда.
ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости. Для решения вопросов о сходимости на границах интервала необходимо проводить дополнительные исследования степенного ряда.
Радиус сходимости вычисляется по формуле
 или
или 
Для рядов по степеням (x-x0)центр интервала сходимости смещается в точку x0 - (x0 – R; x0 + R)
Рассмотрим пример.
Найти интервалы сходимости ряда: 
Коэффициенты ряда: 
Вычислим радиус сходимости

Радиус сходимости бесконечен, следовательно, ряд сходится на всей числовой оси.

Рис. 8.17 - Интервал сходимости функционального ряда.
Таким образом, радиус сходимости бесконечен, следовательно, ряд сходится на всей числовой оси.
Примеры решения заданий в системе MATHCAD
Задача № 1
Исследовать ряд на сходимость 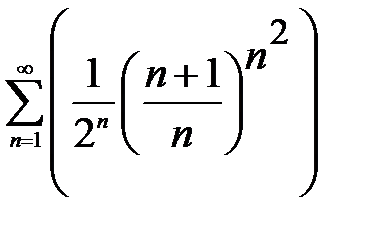

Задача № 2
Найти интервалы сходимости ряда: 
Это ряд по степеням (x +1), значит, центром области сходимости будет точка x0 = -1.
Коэффициенты ряда: 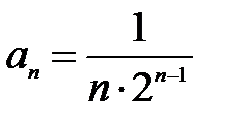
Радиус сходимости:
 .
.
Следовательно, интервал сходимости ряда - (-3;1).

Задача № 3
Разложить функцию y(x) = x2 в ряд Фурье на интервале [-p; p].
Задаём функцию f(x): = x2.
Так как функция чётная достаточно вычислить один коэффициент



Варианты заданий к лабораторной работе № 8
Завдання 1. Дослідити на збіжність числові ряди: а) за ознакою Даламбера; б) за інтегральною ознакою Коші; в) за ознакою порівняння; г) на умовну та абсолютну збіжність.
| № | а | б | в | г |

| 
| 
| 
| |

| 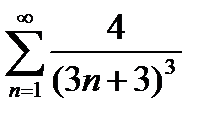
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 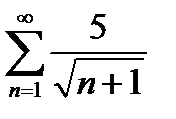
| 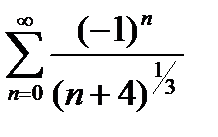
| |

| 
| 
| 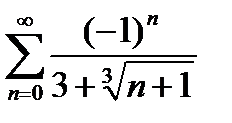
| |

| 
| 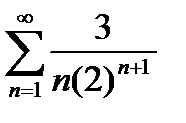
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 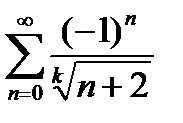
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |
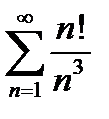
| 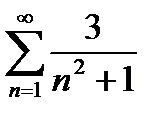
| 
| 
| |

| 
| 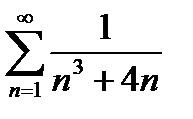
| 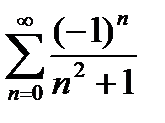
| |
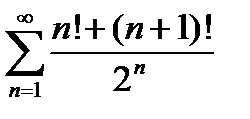
| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 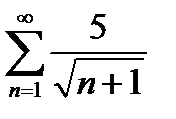
| 
| |

| 
| 
| 
| |

| 
| 
| 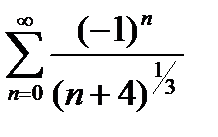
|
Завдання 2. Знайти область збіжності степеневого ряду.
| № | № | ||

| 
| ||

| 
| ||
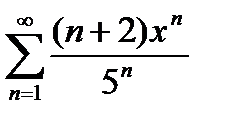
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
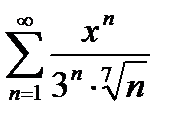
| 
| ||

| 
| ||

| 
| ||

| 
| ||
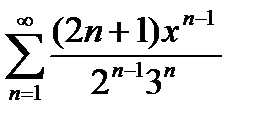
| 
| ||

| 
| ||
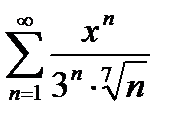
| 
|
Задание 3
Разложить функцию в ряд Фурье на интервале (- π, π)
| № | № | ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
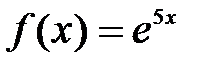
| 
| ||

| 
| ||

| 
| ||

| 
|
ЛИТЕРАТУРА
1. Дьяконов В.П. Mathcad 11/12/13 в математике. – М.: Горячая линия – Телеком, 2007. – 958 с., ил.
2. Денисов-Винский Н.Д., Ерохин С.В. Математика I курс. I семестр. Учебное пособие для студентов. Специальность 140211 «Электроснабжение». – М.: МИЭЭ, 2007.
3. Денисов-Винский Н.Д., Ерохин С.В. Математика I курс. II семестр. Учебное пособие для студентов. Специальность 140211 «Электроснабжение». – М.: МИЭЭ, 2007.
4. Денисов-Винский Н.Д., Ерохин С.В. Математика II курс. Учебное пособие для студентов. Специальность 140211 «Электроснабжение». – М.: МИЭЭ, 2007.
5. Денисов-Винский Н.Д. Mathcad при решении задач по курсу математика. I курс. Учебное пособие для студентов. Специальность 140211 «Электроснабжение». – М.: МИЭЭ, 2007.
6. Сеидова С-Ф. Г. Mathcad в помощь студентам высших учебный заведений. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2007.
7. Сеидова С-Ф. Г. Решение задач высшей математики при помощи системы Mathcad. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2008.