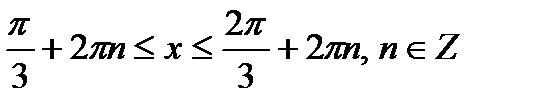Простейшие тригонометрические неравенства

Практическая работа №7

Тема. Решение простейших тригонометрических неравенств.

Цель работы: Сформировать навыки решения простейших тригонометрических неравенств

Простейшие тригонометрические неравенства

Два тригонометрических выражения, соединённые между собой знаком или >, называются тригонометрическими неравенствами.

Решить тригонометрическое неравенство – это значит, найти множество значений неизвестных, входящих в неравенство, при которых неравенство выполняется.

Основная часть тригонометрических неравенств решается сведением их к решению простейших:

· (, , ),

· (, , ),

· (, , ),

· (, , ).

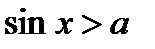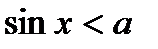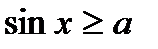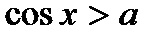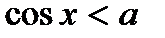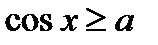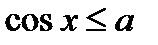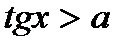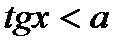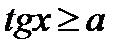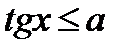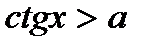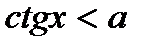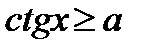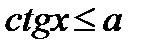Это может быть метод разложения на множители, замены переменного (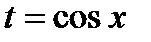, 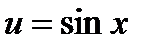и т.д.), где сначала решается обычное неравенство, а затем неравенство вида 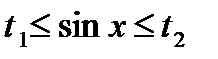и т.д., или другие способы.

Простейшие неравенства решаются двумя способами: с помощью единичной окружности или графически.

Пусть f(х) – одна из основных тригонометрических функций. Для решения неравенства 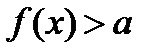достаточно найти его решение на одном периоде, т.е. на любом отрезке, длина которого равна периоду функции f(x). Тогда решением исходного неравенства будут все найденные x, а также те значения, которые отличаются от найденных на любое целое число периодов функции. При этом удобно использовать графический метод.

Приведем пример алгоритма решения неравенств 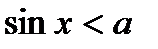(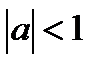) и .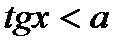

Алгоритм решения неравенства ().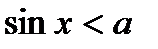

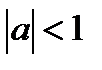1. Сформулируйте определение синуса числа x на единичной окружности.

2. Нарисуйте единичную окружность.

3. На оси ординат отметьте точку с координатой a.

4. Через данную точку проведите прямую, параллельную оси OX, и отметьте точки пересечения ее с окружностью.

5. Выделите дугу окружности, все точки которой имеют ординату, меньшую a.

6. Укажите направление обхода (против часовой стрелки) и запишите ответ, добавив к концам промежутка период функции 2πn, .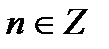

Алгоритм решения неравенства .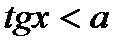

1. Сформулируйте определение тангенса числа x на единичной окружности.

2. Нарисуйте единичную окружность.

3. Проведите линию тангенсов и на ней отметьте точку с ординатой a.

4. Соедините данную точку с началом координат и отметьте точку пересечения полученного отрезка с единичной окружностью.

5. Выделите дугу окружности, все точки которой имеют на линии тангенсов ординату, меньшую a.

6. Укажите направление обхода и запишите ответ с учетом области определения функции, добавив период πn, 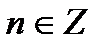(число, стоящее в записи слева, всегда меньше числа, стоящего справа).

Пример 1. Решите неравенство .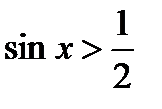

На единичной окружности проводим прямую 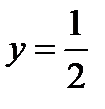, которая пересекает окружность в точках A и B.

Все значения y на промежутке NM больше 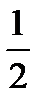, все точки дуги AMB удовлетворяют данному неравенству. При всех углах поворота, больших 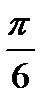, но меньших 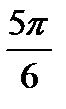, 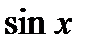будет принимать значения больше 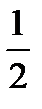(но не больше единицы).

0,5

-0,5

-1

-3

-2

-1

p

p

p

-7

p

;

;

y=

N

M

A

B

Рис.1

Таким образом, решением неравенства будут все значения на интервале 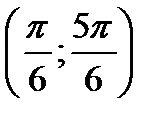, т.е. 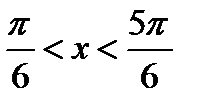. Для того, чтобы получить все решения данного неравенства, достаточно к концам этого промежутка прибавить 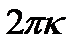, где , т.е. , . Заметим, что значения 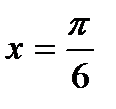и 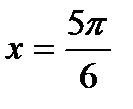являются корнями уравнения ,

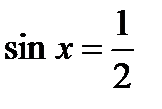т.е. ; .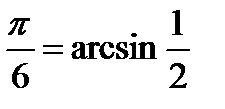

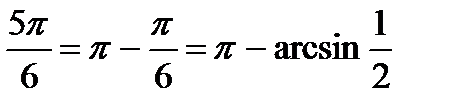Ответ: , .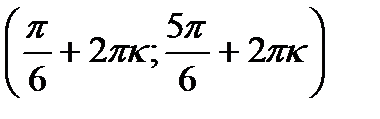

 

Графический метод

На практике довольно часто оказывается полезным графический метод решения тригонометрических неравенств. Рассмотрим сущность метода на примере неравенства :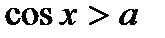

1. Если аргумент – сложный (отличен от х), то заменяем его на t.

2. Строим в одной координатной плоскости tOy графики функци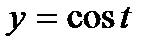й и .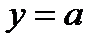

3. Находим такие две соседние точки пересечения графиков, между которыми синусоида располагается выше прямой 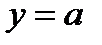. Находим абсциссы этих точек.

4. Записываем двойное неравенство для аргумента t, учитывая период косинуса (t будет между найденными абсциссами).

5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.

Пример 2. Решить неравенство: .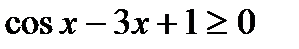

При решении неравенств графическим методом необходимо как можно более точно построить графики функций. Преобразуем неравенство к виду:

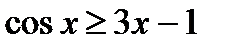
Построим в одной системе координат графики функци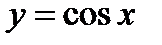й и 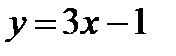(рис. 2).

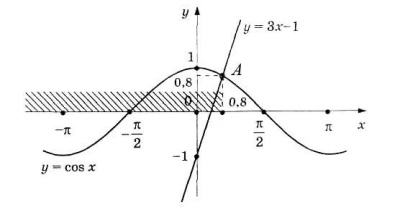
Рис.2

Графики функций пересекаются в точке А с координатами 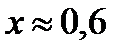; 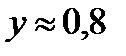. На промежутке 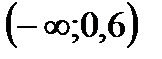точки графика 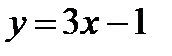ниже точек графика 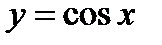. А при 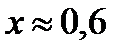значения функции совпадают. Поэтому 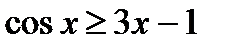при .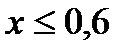

Ответ: .

Алгебраический метод

Довольно часто исходное тригонометрическое неравенство путем удачно выбранной подстановки удается свести к алгебраическому (рациональному или иррациональному) неравенству. Данный метод подразумевает преобразование неравенства, введение подстановки или замену переменной.

Рассмотрим на конкретных примерах применение этого метода.

Пример 3. Приведение к простейшему виду .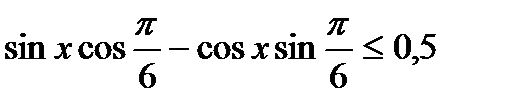

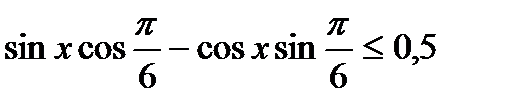
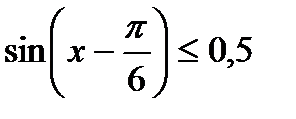(рис. 3)

Рис.3

, .

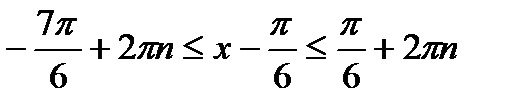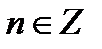Ответ: ,

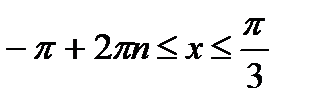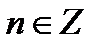
Пример 4. Решить неравенство: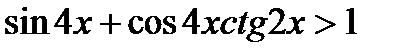

ОДЗ: , .

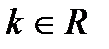Используя формулы: ,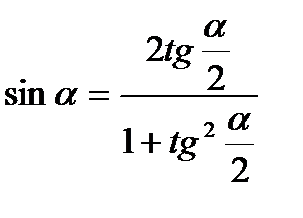

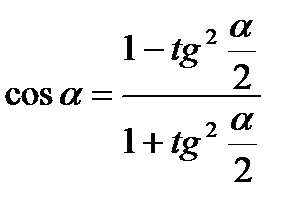
запишем неравенство в виде: .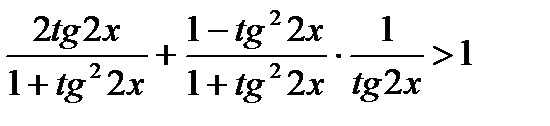

Или, полагая 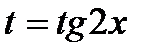после несложных преобразований получим

,

,

.

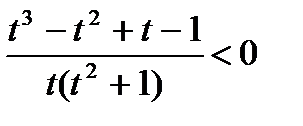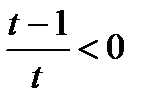Решая последнее неравенство методом интервалов, получаем:

Рис.4

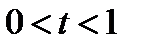, соответственно 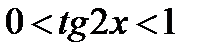. Тогда из рис. 4 следует 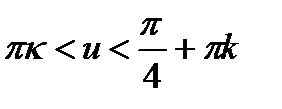, где .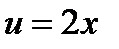

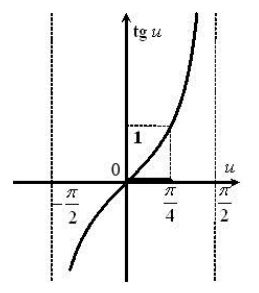
Рис.5

Ответ: , .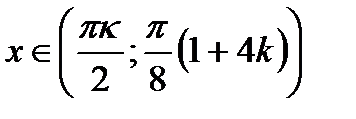

 

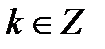Пример 5. Решить неравенство .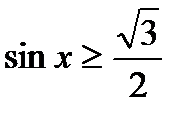

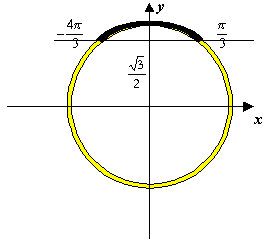
Шаг 1. Начертим единичную окружность, отметим на оси ординат точку 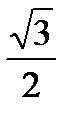и проведем через нее прямую, параллельную оси абсцисс. Эта прямая пересечет единичную окружность в двух точках. Каждая из этих точек изображает числа, синус которых равен .

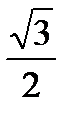Шаг 2. Эта прямая разделила окружность на две дуги. Выделим ту из них, на которой изображаются числа, имеющие синус больший, чем 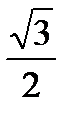. Естественно, эта дуга расположена выше проведенной прямой.

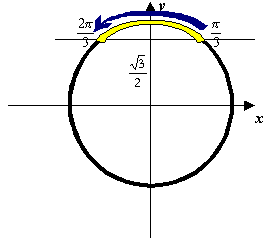
Рис. 2

Шаг 3. Выберем один из концов отмеченной дуги. Запишем одно из чисел, которое изображается этой точкой единичной окружности .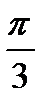

Шаг 4. Для того чтобы выбрать число, соответствующее второму концу выделенной дуги, "пройдем" по этой дуге из названного конца к другому. При этом напомним, что при движении против часовой стрелки числа, которые мы будем проходить, увеличиваются (при движении в противоположном направлении числа уменьшались бы). Запишем число, которое изображается на единичной окружности вторым концом отмеченной дуги .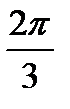

Таким образом, мы видим, что неравенству 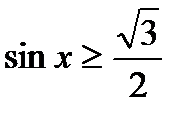удовлетворяют числа, для которых справедливо неравенство 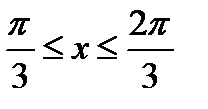. Мы решили неравенство для чисел, расположенных на одном периоде функции синус. Поэтому все решения неравенства могут быть записаны в виде