17. Длина свободного пробега. Среднее число столкновения молекул. Длина свободного пробега молекулы — это среднее расстояние (обозначаемое 
), которое частица пролетает за время свободного пробега от одного столкновения до следующего.Длина свободного пробега каждой молекулы различна, поэтому в кинетической теории вводится понятие средней длины свободного пробега (<λ>). Величина <λ> является характеристикой всей совокупности молекул газа при заданных значениях давления и температуры.
, где 
— эффективное сечение молекулы,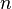 
— концентрация молекул.
среднее число столкновений:
18. Явления переноса.Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное взаимопроникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел. Диффузия сводится к переносу массы, возникает и продолжается до тех пор, пока на границе соприкосновения двух сред градиент плотности отличен от нуля. Количественно явление диффузии подчиняется закону Фика:
,
Теплопроводность. Если в одной области газа температура больше,чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, то есть процесс выравнивания температуры. Этот процесс переноса энергии, называемый теплопроводностью, возникает и продолжается до тех пор, пока на границе соприкосновения двух частей газа градиент температуры отличен от нуля.
Количественно теплопроводность подчиняется закону Фурье:
, Вязкость. Вязкость это свойство жидкости или газа, обусловленное внутренним трением между соприкасающимися параллельными слоями жидкости или газа, движущимися с различными скоростями. В результате, импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Другими словами, внутреннее трение приводит к переносу импульса от одного движущегося слоя жидкости или газа к другому соприкасающемуся с ним слою.
Количественно сила внутреннего трения между двумя соприкасающимися слоями жидкости или газа подчиняется закону Ньютона:
,
19. Реалюные газы. Силы межмолекулярного взаимодействия. Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.
Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:
Силы. Если бы между молекулами не существовало сил притяжения, то все тела при любых условиях находились бы только газообразном состоянии. Но одни силы притяжения не могут обеспечить существования устойчивых образований из атомов и молекул. На очень малых расстояниях между молекулами обязательно действуют силы отталкивания. Благодаря этому молекулы не проникают друг в друга и куски вещества никогда не сжимаются до размеров одной молекулы. Молекула - это сложная система, состоящая из отдельных заряженных частиц: электронов и атомных ядер. Хотя в целом молекулы электрически нейтральны, тем не менее между ними на малых расстояниях действуют значительные электрические силы: происходит взаимодействие электронов и атомных ядер соседних молекул. Если молекулы находятся на растояниях, превышающих их размеры в несколько раз, то силы взаимодействия практически не сказываются. Силы между электрически нейтральными молекулами являются короткодействующими. На расстояниях, превышающих 2 - 3 диаметра молекул, действуют силы притяжения. По мере уменьшения расстояния между молекулами сила притяжения сначала увеличивается, а затем начинает убывать и убывает до нуля, когда расстояние между двумя молекулами становится равным сумме радиусов молекул. При дальнейшем уменьшении расстояния электронные оболочки атомов начинают перекрываться, и между молекулами возникают быстро нарастающие силы отталкивания.
20. Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.
Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давленияхи высоких температурах, в других условиях её соответствие с опытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут.
Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия 
становится функцией не только температуры, но и объёма.
где
· 
— давление,
· 
— молярный объём,
· 
— абсолютная температура,
· 
— универсальная газовая постоянная.
21. Эзотермы Эндрюса. Английский физик Эндрюс во второй половине прошлого века произвел ряд исследований свойств паров и построил экспериментальные изотермы. В толстостенный цилиндр под поршнем вводились пары углекислого CO2, давление измерялось при помощи манометра.
При изотермическом уменьшении объема давление возрастало и на графике, соответствующем данному процессу (рис. 3.2), получался участок изотермы 1-2, приближающийся к гиперболе. Таким образом опыты Эндрюса подтвердили, что ненасыщающие пары подчиняются закону Бойля - Мариотта. Точка 2 соответствует объему V2 и показывает состояние паров CO2, при котором они насыщают пространство. При дальнейшем уменьшении объема в цилиндре часть паров переходит в жидкость, а давление оставшихся над жидкостью паров сохраняется при данной температуре неизменным. На графике получается участок 2-3, соответствующий одновременному существованию вещества в двух фазах (в двух агрегатных состояниях) - жидкой и газообразной.
Точка 3 соответствует объему V3 и показывает такое состояние, когда пар полностью обращается в жидкость. Дальнейшее увеличение давления вызывает сжатие жидкости, а так как жидкости крайне слабо сжимаются, участок изотермы 3-4 представляет почти вертикальную линию, лишь незначительно приближающуюся к оси Y.
На рис. 3.3. показан ряд таких изотерм, соответствующих одной и той же массе CO2, но построенных для разных температур. Чем выше температура, тем участок 2-3 короче, т.е. разность в объемах насыщающего пара (V2) и полученной из него при полной конденсации жидкости (V3) становится меньше.
При некоторой определенной температуре площадка 2-3 исчезает, на графике возникает точка перегиба K, которая носит название критической точки. Температура, при которой она получается, называется критической температурой (Tк), давление, соответствующее точке K - критическим давлением (pк), а объем, занимаемый при этом молем газа - критическим объемом (Vк). При критической температуре ненасыщающий пар переходит в жидкое состояние, как бы минуя стадию насыщения. Для CO2 критическая температура равна 31˚C, критическое давление около 73 атм.
22. Изотермы Ван-дер-Ваальса. Фазовые диаграммы. Фазовые переходы. Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса – кривые зависимости ρ от Vm при заданных Т, определяемые уравнением Ван-дер-Ваальса (9.2) для молягаза. Эти кривые (рассматриваются для четырех различных температур (рис. 9.2)), имеют довольно своеобразный характер.
При высоких температурах (Т > Тк) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре Тк на изотерме имеется лишь одна точка перегиба К.
Рис.9.2 Эта изотерма называется критической, соответствующая ей температура Тк – критической температурой; точка перегиба К называется критической точкой; в этой точке касательная к ней параллельна оси абсцисс.
Соответствующие этой точке объем VK и давление рк называются также критическими. Состояние с критическими параметрами (рк, Vк, Тк) называется критическим состоянием. При низких температурах (Τ < Τк)изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.
Для пояснения характера изотерм преобразуем уравнение (9.2) к виду:
pV3m - (RT + pb) V2m + aVm - ab = 0. (9.3)
Уравнение (9.3) при заданных р и Τ является уравнением третьей степени относительно Vm; оно может иметь либо три вещественных корня, либо один вещественный и два мнимых, причем физический смысл имеют лишь вещественные положительные корни. Поэтому первому случаю соответствуют изотермы при низких температурах (три значения объема газа V 1, V 2и V 3отвечают (символ «m » для простоты опускаем) одному значению давления р),второму случаю – изотермы при высоких температурах. Фа́зовая диагра́мма (диаграмма состоя́ния) — графическое отображение равновесного состояния бесконечной физико-химической системы при условиях, отвечающих координатам рассматриваемой точки на диаграмме (носит название фигуративной точки). Обычными координатами для построения фазовой диаграммы являются термодинамические параметры — температура и давление — и состав системы (в мольных или массовых процентах).
В общем случае количество координат превышает число компонентов системы на единицу (диаграмма однокомпонентной системы двумерна, двухкомпонентной — трёхмерна и т. п.) Для конденсированных систем зачастую не учитывают изменение фазовых равновесий за счёт давления, в этом случае число измерений диаграммы равно числу компонентов (диаграмма конденсированной двухкомпонентной системы двумерна, трёхкомпонентной — трёхмерна и т. п.) Сложные фазовые диаграммы в печатных изданиях изображают в виде сечений или проекций.
Согласно правилу фаз, на двумерной диаграмме однофазная область описывается полем, двухфазная — линией (на p-T диаграммах) или набором параллельных линий конод, для которых фиксированы составы равновесных фаз (на диаграммах с участием состава), трёхфазная — точкой (на p-T диаграммах) или горизонталью (на T-x или p-x диаграммах).
Фа́зовый перехо́д (фазовое превращение) в термодинамике — переход вещества из одной термодинамической фазы в другую при изменении внешних условий. С точки зрения движения системы по фазовой диаграмме при изменении её интенсивных параметров (температуры, давления и т. п.), фазовый переход происходит, когда система пересекает линию, разделяющую две фазы. Поскольку разные термодинамические фазы описываются различными уравнениями состояния, всегда можно найти величину, которая скачкообразно меняется при фазовом переходе.
Поскольку разделение на термодинамические фазы — более мелкая классификация состояний, чем разделение по агрегатным состояниям вещества, то далеко не каждый фазовый переход сопровождается сменой агрегатного состояния. Однако любая смена агрегатного состояния есть фазовый переход.
Наиболее часто рассматриваются фазовые переходы при изменении температуры, но при постоянном давлении (как правило равном 1 атмосфере). Именно поэтому часто употребляют термины «точка» (а не линия) фазового перехода, температура плавления и т. д. Разумеется, фазовый переход может происходить и при изменении давления, и при постоянных температуре и давлении, но и при изменении концентрации компонентов (например, появление кристалликов соли в растворе, который достиг насыщения).
23. Д ЖОУЛЯ - ТОМСОНА ЭФФЕКТ - изменение темп-ры газа при стационарном адиабатич. протекании его через пористую перегородку. Обнаружен и исследован Дж. П. Джоулем и У. Томсоном (W. Thomson) в 1852-62. В процессе Джоуля-Томсона газ, к-рый первоначально занимал объём V1 при давлении P1, перетекает через пористую перегородку, занимая после перехода объём V2 при давлении P2. Над системой совершается работа P1V1-P2V2, равная изменению внутр. энергии газа U2-U1, поскольку пористая перегородка гасит все его макроскопич. движения. Следовательно, при протекании газа в условиях тепловой изоляции остаётся постоянной энтальпия 
. Из условия постоянства H следует, что изменение темп-ры T на единицу давления (дифференциальный Д.-T. э.) равно
Гипотеза Бройля.
В 1924г. Луи де Бройль выдвинул гипотезу: корпускулярно-волновая двойственность свойств, установленная для света, имеет универсальный характер. Все частицы, имеющие конечный импульс, обладают волновыми свойствами. Движению частиц соответствует некоторый волновой процесс.
С каждым движущимся микрообъектом связываются корпускулярные характеристики: энергия E и импульс 
и волновые характеристики - длина волны λ или частота ν. Полная энергия частицы и ее импульс определятся формулами
; (1.1.1)
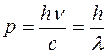. (1.1.2)
Длина волны, связанной с движущейся частицей, определится выражением
. (1.1.3)
Выражение (1.1.3) называется формулой де Бройля.
25. Подтверждение гипотезы де Бройля. Впервые гипотеза де Бройля была подтверждена экспериментально в опытах по дифракции электронов американскими физиками К. Дэвиссоном (C.Devisson) и Л. Джермером (L. Germer). Схема опыта представлена на рис.2. Параллельный моноэнергетический пучок электронов, получаемый с помощью электронно-лучевой трубки 1, направляется на мишень 2 (монокристалл никеля). Отраженные электроны улавливаются коллектором 3, соединенным с гальванометром. Коллектор можно устанавливать под любым углом относительно падающего луча.
Рассмотрим результаты опытов Дэвиссона и Джермера. Например, в одном из опытов наблюдалась дифракция электронов с энергией 54 эВ. Первый дифракционный максимум наблюдался под углом j = 50о (см. рис.2). Импульс электрона связан с его кинетической энергией формулой 
. Из формулы де Бройля определяем длину волны электронов:
В то же время по формуле Брегга для максимума первого порядка при дифракции на кристалле никеля с периодом решетки d = 0,091 нм получаем:
Оба результата хорошо совпадают, что подтверждает наличие волновых свойств у электронов.
Экспериментальная проверка волновой природы частиц продолжалась и в последующие годы. В 1928 - 30 гг. О. Штерн (O. Stern) и И. Эстерман (I. Estermann) провели опыты по дифракции атомов гелия, неона, молекул водорода и дейтерия на кристаллах.
26. Соотношение неопределенностей. Микрочастицы в одних случаях проявляют себя как волны, в других как корпускулы. К ним не применимы законы классической физики частиц и волн. В квантовой физике доказывается, что к микрочастице нельзя применять понятие траектории, но можно сказать, что частица находится в данном объеме пространства с некоторой вероятностью Р. Уменьшая объем, мы будем уменьшать вероятность обнаружить частицу в нем. Вероятностное описание траектории (или положения) частицы приводит к тому, что импульс и, следовательно, скорость частицы может быть определена с какой-то определенной точностью.
Далее, нельзя говорить о длине волны в данной точке пространства и отсюда следует, что если мы точно задаем координату Х, то мы ничего не сможем сказать о импульсе частицы, т.к. 
. Только рассматривая протяженный участок DC мы сможем определить импульс частицы. Чем больше DC, тем точнее D р и наоборот, чем меньше DC, тем больше неопределенность в нахождении D р.
Соотношение неопределенностей Гейзенберга устанавливает границу в одновременном определении точности канонически сопряженных величин, к которым относятся координата и импульс, энергия и время.
27. Волновая функция и ее физический смысл. Дифракционная картина, наблюдающаяся для микрочастиц, характеризуется неодинаковым распределением потоков микрочастиц в различных направлениях - имеются минимумы и максимумы в других направлениях. Наличие максимумов в дифракционной картине означает, что в этих направлениях распределяются волны де Бройля с наибольшей интенсивностью. А интенсивность будет максимальной, если в этом направлении распространяется максимальное число частиц. Т.е. дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности в распределении частиц: где интенсивность волны де Бройля максимальная, там и частиц больше.
Волны де Бройля в квантовой механике рассматриваются как волнывероятности, т.е. вероятность обнаружить частицу в различных точках пространства меняется по волновому закону (т.е. ~ е - iωt ). Но для некоторых точек пространства такая вероятность будет отрицательной (т.е. частица не попадает в эту область). М. Борн (немецкий физик) предположил, что по волновому закону меняется не сама вероятность, а амплитуда вероятности, которую также называют волновой функцией или y-функцией (пси - функцией).
Волновая функция - функция координат и времени.
28. Принцип квантовой суперпозиции. принцип существования суперпозиций состояний обычно называется в контексте квантовой механики просто принципом суперпозиции.
Если функции 
и 
являются допустимыми волновыми функциями, описывающими состояние квантовой системы, то их линейная суперпозиция, 
, также описывает какое-то состояние данной системы. Если измерение какой-либо физической величины 
в состоянии 
приводит к определённому результату 
, а в состоянии 
— к результату 
, то измерение в состоянии 
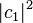приведёт к результату или с вероятностями 
и 
соответственно.
Из принципа суперпозиции также следует, что все уравнения на волновые функции (например, уравнение Шрёдингера) в квантовой механике должны быть линейными.
29. Решение уравнения Шредингера для свободной частицы. Для свободной частицы потенциальная энергия U ≡ 0. Уравнение Шредингера (7.3) в этом случае выглядит следующим образом:
Для частицы, движущейся вдоль оси х, волновая функция ψ = ψ(х) и уравнение еще упрощается:
Решением этого уравнения будет экспоненциальная функция:
проверить это легко прямой подстановкой. При этом для энергии E получаем, как и следовало ожидать,
здесь px = mv - импульс частицы.
30. Частица в потенциальной яме с бесконечно высокими стенками. Если поместить частицу в потенциальную яму, то непрерывный спектр энергий становится дискретным. Для уравнения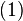 
с потенциальной энергией 
, которая равна нулю в интервале 
и становится бесконечной в точках 
и 
. На этом интервале уравнение Шрёдингера совпадает с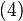 
. Граничные условия 
, 
для волновой функции запишутся в виде
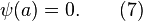
Ищем решения в виде 
. С учётом граничных условий получаем для собственных значений энергии 
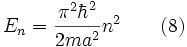
и собственных функций с учётом нормировки
31. Гармонический осциллятор в квантовой механике представляет собой квантовый аналог простого гармонического осциллятора, при этом рассматривают не силы, действующие на частицу, а гамильтониан, то есть полную энергию гармонического осциллятора, причём потенциальная энергия предполагается квадратично зависящей от координат. Учёт следующих слагаемых в разложении потенциальной энергии по координате ведёт к понятию ангармонического осциллятора.
Модель квантового гармонического осциллятора служит первым приближением для описания колебательного движения в молекулах. Для более точных расчетов (например, при больших амплитудах колебаний) могут быть использованы более точные модели потенциалов, например, потенциал Морзе.
Квантовый гармонический осциллятор — одна из немногих систем в квантовой механике, для которой может быть получено точное решение уравнения Шрёдингера.
32. Прохождение частиц через потенциальный барьер туннельный эффект. Ра ссмотрим простейший потенциальный барьер прямоугольной формы. Для одномерного (по оси х) движения частицы.
ì∞,x<0 (для области 1)
U(x)=í0,0≤x≤l (для области 2)
î0,x>1 (для области 3)
где l-ширина ямы, а энергия отсчитывается от ее дна, U-высота. Частица, обладая энергией Е, либо беспрепятственно пройдет над барьером(при Е>U), либо отразится от него (при Е<U) и будет двигаться в обратную сторону. Для микрочастица, даже при Е>U, имеется вероятность отражения от барьера, и при Е<U есть вероятность проникновения через барьер. Это слудет из решения ур-ния Шредингера, описывающего движение микрочастицы
для областей 1 и 3 k2=2mE/h2 ; для области 2 q2=2m(E-U)/h2
Общие решения этих диф.уравнений:
Ψ1(x)=A1eikx+B1e-ikx(для области 1);Ψ2(x)=A2eiqx+B2e-iqx(для области2) Ψ3(x)=A3eikx+B3e-ikx(для области 3).
В частности, для области 1 полная волновая, будет иметь вид ψ1(x,t)=ψ1(x)e-(i/h)Et=A1e-(i/h)(Et-px)+B1x-(i/h)(Et+px) (в этом выражении первый член представляет собой плоскую волну вдоль х, другой – волну, распространяющаяся в обратную сторону). В области 3 есть только прошедшая сквозь барьер волна и поэтому В3=0.Для области 2 q=iβ;β=√2m(E-U) /h.
Получили Ψ1(x)=A1eikx+B1e-ikx, Ψ2(x)=A2e-βx+B2eβx,Ψ3(x)=A3eikx
Качественный характер функций ψ1(х),ψ2(х),ψ3(х)(см.рис2), откуда следует, что волновая функция не равна нулю и внутри барьера, а в области3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т.е. с той же частотой, но с меньшей амплитудой. Т.о. приходим к явлению – туннельный эффект, когда микрочастица может пройти сквозь потенциальный барьер.
33. Строение многоэлектронных атомов.Электронные конфигурации элемента. Запись распределения электронов в атоме по уровням, подуровням и орбиталям называется электронной конфигурацией элемента. Обычно электронная конфигурация приводится для основного состояния атома. При записи электронной конфигурации указывают цифрами главное квантовое число (n), буквами – орбитальное квантовое число (l). Количество электронов на подуровне обозначают числом в виде степени буквенного обозначения подуровня. Например, электронная конфигурация водорода Н − 1 s 1, магния Mg – 1 s 22 s 22 p 63 s 2, титана Ti – 1 s 22 s2 2 p 6 3 s 23 p 63 d 24 s 2.
При составлении электронных конфигураций многоэлектронных атомов учитывают: принцип наименьшей энергии, принцип Паули, правила Гунда и Клечковского.
Принцип наименьшей энергии. Современная теория строения атома позволила объяснить электронную структуру всех элементов и показала, что конфигурация электронной структуры невозбужденного атома однозначно определяется зарядом ядра. При заполнении электронами уровней и подуровней последовательность размещения электронов в атоме должна отвечать как наименьшей энергии электрона, так и наименьшей энергии атома в целом. Наиболее устойчивым состоянием атома является такое, в котором электроны находятся на наиболее близких ядру энергетических уровнях.
При переходе от одного элемента к другому электроны будут постепенно заполнять подуровни и уровни в порядке возрастания их энергии. Однако вследствие взаимодействия электронов между собой в многоэлектронных атомах порядок заполнения уровней и подуровней отличается от ожидаемого в соответствии с расположением энергетических уровней в атоме водорода. Правило суммы (n + l) позволяет предвидеть отличия в расположении энергетических уровней у многоэлектронных атомов от атома водорода.
Правило Клечковского. Увеличение энергии и соответственно заполнение орбиталей происходит в порядке возрастания суммы квантовых чисел (n+l), а при равной сумме (n+l) – в порядке возрастания числа n.
Согласно этому правилу последовательность заполнения электронами уровней и подуровней имеет следующий вид:
1 s <2 s < 2р <3 s <3 р < 4s<3d < 4р<5s <4 d <5 p <6 s <4 f ≈5 d <6 p <7 s <5 f ≈6 d <7 p.
Последовательность возрастания энергии определена опытным путем и называется шкалой энергии. Спин в квантовой механике обозначает собственный момент импульса отдельных элементарных частиц и их связанных состояний в виде ядер и атомов. В отличие от орбитального момента импульса, спин не связан с перемещением в пространстве центра инерции частицы, и является её внутренней характеристикой. Поскольку спин является вектором, он имеет направление в пространстве и отражает вращение составных элементов частицы. У ядер и атомов спин определяется по правилам квантовой механики как векторная сумма орбитальных и спиновых моментов импульса составляющих частиц, с учётом квантования проекций моментов импульса. При увеличении размеров системы и количества частиц в ней орбитальные моменты импульса могут быть много больше, чем спиновые моменты импульса. Это приводит к тому, что спин макросистемы в виде отдельного тела почти полностью зависит от орбитального вращения элементов вещества тела вокруг некоторой оси.
В квантовой механике квантовые числа для спина не совпадают с квантовыми числами для орбитального момента частиц, что приводит к неклассической трактовке спина. Кроме этого, у спина и орбитального момента частиц возникает различная связь с соответствующими магнитными дипольными моментами, сопровождающими любое вращение заряженных частиц. В частности, в формуле для спина и его магнитного момента гиромагнитное отношение не равно 1.
Концепция спина у электрона привлекается для объяснения многих явлений, таких как расположение атомов в периодической системе химических элементов, тонкая структура атомных спектров, эффект Зеемана, ферромагнетизм, а также для обоснования принципа Паули. Недавно возникшая область исследований, называемая «спинтроника», занимается манипуляциями спинов зарядов в полупроводниковых устройствах. В ядерном магнитном резонансе используется взаимодействие радиоволн со спинами ядер, позволяющее осуществлять спектроскопию химических элементов и получать изображения внутренних органов в медицинской практике. Для фотонов как частиц света спин связывается с поляризацией света. Математическая теория спина была использована для построения теории изоспина элементарных частиц.
34. Атом водорода в квантовой механике. Уравнением движения микрочастицы в различных силовых полях является волновое уравнение Шредингера.
Для стационарных состояний уравнение Шредингера будет таким:
, m – масса частицы, h – постоянная Планка, E – полная энергия, U – потенциальная энергия.
Уравнение Шредингера является дифференциальным уравнением второго порядка и имеет решение, которое указывает на то, что в атоме водорода полная энергия должна иметь дискретный характер:
E1, E2 , E3…
Эта энергия находится на соответствующих уровнях n =1,2,3,…по формуле:
Самый нижний уровень E соответствует минимальной возможной энергии. Этот уровень называют основным, все остальные – возбужденными.
По мере роста главного квантового числа n энергетические уровни располагаются теснее, полная энергия уменьшается, и при n = E>0 электрон становится свободным, несвязанным с конкретным ядром, а атом – ионизированным.
Полное описание состояния электрона в атоме, помимо энергии, связано с четырьмя характеристиками, которые называются квантовыми числами. К ним относятся: главное квантовое число п, орбитальное квантовое число l, магнитное квантовое число m1, магнитное спиновое квантовое число ms.
трона в пространстве, то есть волновая функция в пространстве характеризуется тремя системами. Каждая из них имеет свои квантовые числа: п, l, ml.
Каждой микрочастице, в том числе и электрону, также свойственно собственное внутреннее сложное движение. Это движение может характеризоваться четвертым квантовым числом ms. Поговорим об этом подробнее.
A. Главное квантовое число п, согласно формуле, определяет энергетические уровни электрона в атоме и может принимать значения п = 1, 2, 3…
Б. Орбитальное квантовое число /. Из решения уравнения Шредингера следует, что момент импульса электрона (его механический орбитальный момент) квантуется, то есть принимает дискретные значения, определяемые формулой
где Ll – момент импульса электрона на орбите, l – орбитальное квантовое число, которое при заданном п принимает значение i = 0, 1, 2… (n – 1) и определяет момент импульса электрона в атоме.
B. Магнитное квантовое число m l. Из решения уравнения Шредингера следует также, что вектор Ll (момент импульса электрона) ориентируется в пространстве под влиянием внешнего магнитного поля. При этом вектор развернется так, что его проекция на направление внешнего магнитного поля будет
Llz = hml
где ml называется магнитным квантовым числом, которое может принимать значения ml = 0, ±1, ±2,±1, то есть всего (2l + 1) значений.
Учитывая сказанное, можно сделать заключение о том, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях (n – одно и то же, а l и ml – разные).
При движении электрона в атоме электрон заметно проявляет волновые свойства. Поэтому квантовая электроника вообще отказывается от классических представлений об электронных орбитах. Речь идет об определении вероятного места нахождения электрона на орбите, то есть местонахождение электрона может быть представлено условным «облаком». Электрон при своем движении как бы «размазан» по всему объему этого «облака». Квантовые числа n и l характеризуют размер и форму электронного «облака», а квантовое число ml – ориентацию этого «облака» в пространстве.
В 1925 г. американские физики Уленбек и Гаудсмит доказали, что электрон также обладает собственным моментом импульса (спином), хотя мы не считаем электрон сложной микрочастицей. Позднее выяснилось, что спином обладают протоны, нейтроны, фотоны и другие элементарные частицы
Опыты Штерна, Герлаха и других физиков привели к необходимости характеризовать электрон (и микрочастицы вообще) добавочной внутренней степенью свободы. Отсюда для полного описания состояния электрона в атоме необходимо задавать четыре квантовых числа: главное – п, орбитальное – l, магнитное – ml, магнитное спиновое число – ms.
В квантовой физике установлено, что так называемая симметрия или асимметрия волновых функций определяется спином частицы. В зависимости от характера симметрии частиц все элементарные частицы и построенные из них атомы и молекулы делятся на два класса. Частицы с полуцелым спином (например, электроны, протоны, нейтроны) описываются асимметричными волновыми функциями и подчиняются статистике Ферми—Дирака. Эти частицы называются фермионами. Частицы с целочисленным спином, в том числе и с нулевым, такие как фотон (Ls =1) или л-мезон (Ls = 0), описываются симметричными волновыми функциями и подчиняются статистике Бозе– Эйнштейна. Эти частицы называются бозонами. Сложные частицы (например, атомные ядра), составленные из нечетного числа фермионов, также являются фермионами (суммарный спин – полуцелый), а составленные из четного – бозонами (суммарный спин – целочисленный).
35. Рентгеновские спектры. Спектры испускания и поглощения рентгеновских лучей (См.Рентгеновские лучи), т. е. электромагнитного излучения в области длин волн от 10-4до 103 Å. Дляисследования спектров рентгеновского излучения, получаемого, например, в рентгеновской трубке (См.Рентгеновская трубка), применяют спектрометры с кристаллом-анализатором (или дифракционнойрешёткой) либо бескристальную аппаратуру, состоящую из детектора (сцинтилляционного, газовогопропорционального или полупроводникового счётчика) и амплитудного анализатора импульсов (см.Спектральная аппаратура рентгеновская). Для регистрации Р. с. применяют рентгенофотоплёнку иразличные детекторы ионизирующих излучений. Однотипность характеристических спектров обусловлена тем, что внутренние электронные слои у разных атомов одинаковы и отличаются только энергетически из–за силового воздействия со стороны ядер, которое увеличивается с возрастанием порядкового номера элемента. Поэтому характеристические спектры сдвигаются в сторону больших частот с увеличением заряда ядра. Опытно это было подтверждено сотрудником Рентгена – Мозли, который измерил частоты рентгеновских переходов для 33 элементов. Им