1. Поместить в подмножество достижимых состояний начальное состояние.
2. Для каждого состояния, добавленного в подмножество на предыдущем шаге, определить всех преемников и добавить во множество тех из них, которые там еще не представлены.
3. Повторять шаг 2 до тех пор, пока алгоритм не перестанет поставлять новые состояния.
4. Не попавшие в подмножество состояния являются недостижимыми и могут быть удалены из матрицы переходов.
5. Конец алгоритма.
Определение 6. Минимальный автомат – это автомат, который не содержит недостижимых состояний и никакие два его состояния не являются эквивалентными.
Заметим, что наряду с конечными распознавателями рассматривают и так называемые процессоры. В этом случае во входной алфавит добавляется символ «–| » – маркер конца цепочки, а в соответствующий столбец заносится команда (либо вызов специальной функции обработки) „да”, если это допускающее состояние, и „нет”, если состояние отвергающее. Например:
| –| | ||||||||||||||
| A | B | C | A | B | C | нет | ||||||||
| B | A | C | B | A | C | нет | ||||||||
| C | A | F | C | A | F | нет | ||||||||
| D | B | C | D | B | C | нет | ||||||||
| E | B | C | E | B | C | да | ||||||||
| F | D | A | F | D | A | да |
Таблица переходов для Таблица переходов
конечного распознавателя для процессора
5.2. Пример выполнения индивидуального задания
1. Для заданного автомата найдите: самую короткую цепочку, распознаваемую автоматом; три другие цепочки, распознаваемые этим автоматом; три цепочки, которые отвергаются автоматом.
| A | B | C | |
| B | A | C | |
| C | A | F | |
| D | B | F | |
| F | D | A |
 |
Решение. Построим для данного автомата граф переходов, что позволит определять нужные цепочки из входных символов. Состояния, находящиеся в квадрате, являются допускающими, остальные (в кружочках)– отвергающими.
а) Самая короткая цепочка, распознаваемая автоматом  ;
;
б) три другие допустимые цепочки: 011, 0011, 00011;
Например:  – допустимая;
– допустимая;
 – допустимая;
– допустимая;
 – допустимая;
– допустимая;
в) три отвергающие: 01, 100, 11011.
Например:  – отвергающая;
– отвергающая;
 – отвергающая;
– отвергающая;
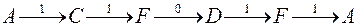 – отвергающая.
– отвергающая.
2. Опишите словами множество цепочек распознаваемых конечным автоматом:
| A | B | С | |
| B | D | B | |
| C | C | D | |
| D | D | D | |
 |
Решение. Построим для данного автомата граф переходов:
Автомат допускает цепочки трех типов:
- цепочки начинаются с 0, затем идет, возможно пустая, последовательность 1, потом следует 0, а далее любая возможно пустая последовательность из 0 и 1;
- цепочки начинаются с 1, затем идет, возможно пустая, последовательность 0, потом следует 1, а далее любая возможно пустая последовательность из 0 и 1;
- пустая цепочка.
3. Для конечного автомата найдите входную цепочку минимальной длины такую, что под ее действием:
а) каждое возможное состояние имеет место хотя бы раз;
б) каждый возможный переход происходит хотя бы раз.
| A | D | A | |
| B | A | C | |
| C | A | F | |
| D | B | C | |
| E | B | C | |
| F | E | A | |
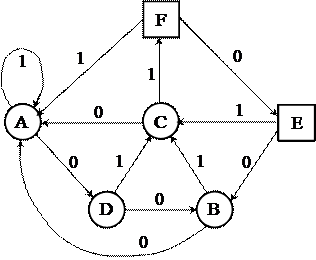 |
Решение. Построим для данного автомата граф переходов:
а) по графу видно, что минимальной цепочкой, в ходе прочтения которой все состояния будут иметь место хотя бы раз, будет:
 ;
;
или, например, такая:
 ;
;
б) из всех возможных прохождений по графу нам нужно взять то, которое пройдет по всем ребрам графа. Это, например, может быть цепочка:

Итак, искомая цепочка: 101110110110000010.
4. Постройте конечный автомат с заданным входным алфавитом, который допускает в точности следующее множество цепочек:
Входную цепочку, содержащую подцепочку "FFAFA", если входной алфавит {F,A}.
Решение. Определим имена и назначение состояний.
А – начальное состояние – отвергающее состояние;
В – в цепочке есть F – 0 – отвергающее состояние;
С– в цепочке есть FF– 0 – отвергающее состояние;
D– в цепочке есть FFA – 0 – отвергающее состояние;
E– в цепочке есть FFAF – 0 – отвергающее состояние;
F– в цепочке есть FFAFA – 1 – допускающее состояние.
Автомат будет иметь следующую матрицу переходов:
| A | F | ||
| A | A | B | |
| B | A | C | |
| C | D | С | |
| D | A | E | |
| E | F | C | |
| F | F | F |
5. Постройте конечный автомат для множества цепочек из нулей и единиц, у которых за каждым вхождением пары 11 следует 0. Минимизируйте его. Затем превратите этот автомат в процессор с концевым маркером.
Решение. Определим смысл и имена состояний:
А – начальное состояние – 1 – допустимое состояние;
В – в цепочке есть 1 – 1 – допустимое состояние;
С – в цепочке есть 11 – 0 – недопустимое состояние;
D – в цепочке есть 110 – 1 – допустимое состояние;
E – состояние ошибки – 0 – недопустимое состояние;
Автомат будет иметь следующую таблицу переходов:
| A | A | B | |
| B | A | C | |
| C | D | E | |
| D | A | B | |
| E | E | E |
Теперь минимизируем его.
a) Начнем с определения недостижимых состояний.
Помещаем во множество достижимых состояний начальное состояние V 0={A}.
И далее следуем указаниям алгоритма:
V 1={A, B}
V 2={A, B, C}
V 3={A, B, C, D, E}
Очевидно, что в автомате нет недостижимых состояний.
b) Теперь найдем эквивалентные состояния (алгоритм б):
Разбиваем все множество состояний на допустимые и недопустимые:
P 0=({A, B, D}, {C, E})
Затем по каждому входному символу разбиваем предыдущее разбиение, если состояния из одного подмножества имеют преемников в разных подмножествах:
0: P 1=({A, B, D}, {C}, {E});
1: P 2=({A, D}, {C}, {B}, {E});
0: P 3=({A, D}, {C}, {B}, {E});
Так как дальнейшее разбиение не происходит, то состояния A и D эквивалентны. Удаляем из автомата состояние D и заменяем его буквой A. Таблица переходов искомого процессора будет иметь вид:
| –| | |||
| A | A | B | да |
| B | A | C | да |
| C | A | нет | нет |
6. Определить, эквивалентны ли два заданных автомата и, если возможно, найти для них различающую цепочку.
| A | D | A | A | B | A | |||||||||||||||
| B | A | C | B | A | C | |||||||||||||||
| C | A | F | C | F | A | |||||||||||||||
| D | B | C | D | B | C | |||||||||||||||
| E | B | C | E | B | C | |||||||||||||||
| F | E | A | F | E | D |
Решение. Два заданных автомата эквивалентны, если эквивалентны их начальные состояния. Меткой каждой строки таблицы эквивалентности является пара проверяемых начальных состояний (для первого и второго автомата). Справа (+/-) – обозначение допустимости/недопустимости состояний (если они оба допустимые или недопустимые, то ставим «+», иначе – «-»).
Далее по каждому входному символу мы записываем пары переходов для каждого автомата по этому символу. Новыми парами помечаем строки в левом столбце. Если исходная пара эквивалентна, то все полученные в ходе проверки пары тоже эквивалентны.
| (A, A) | (D, B) | (A, A) | + |
| (D, B) | (B, A) | (С, C) | + |
| (B, A) | (A, B) | (C, A) | + |
| (С, А) | (А, В) | (F, A) | + |
| (F, A) | – |
Видно, что (F, A) – неэквивалентные состояния для двух автоматов, таким образом, исходная пара (А, А) также неэквивалентна. Из таблицы определим различающую цепочку 0011.
Для первого автомата:  – допустимое состояние.
– допустимое состояние.
Для второго автомата:  – отвергающее состояние.
– отвергающее состояние.
7.Построить минимальный автомат эквивалентный данному.
| A | C | E | G | |
| B | K | E | G | |
| C | J | A | H | |
| D | F | A | G | |
| E | E | J | H | |
| F | D | I | A | |
| G | H | A | J | |
| H | G | J | B | |
| I | D | F | G | |
| J | B | H | G | |
| K | M | E | N | |
| M | J | A | H | |
| N | H | A | J |
Решение. Исходя из определения минимального автомата, необходимо удалить недостижимые и объединить эквивалентные состояния данного автомата. Для определения множества недостижимых состояний вначале найдем множество достижимых состояний2.
1. V 0={A};
2. V 1={A, C, E, G};
3. V 2={A, C, E, G, J, H};
4. V 3={A, C, E, G, J, H, B};
5. V 4={A, C, E, G, J, H, B, K};
6. V 5={A, C, E, G, J, H, B, K, M, N};
7. V 6={A, C, E, G, J, H, B, K, M, N}.
Так как множества, построенные на шаге 6 и 7 совпадают, т. е. алгоритм перестал поставлять новые состояния, то недостижимыми являются те состояния, которые не попали в последнее множество: F, D, I.
Имеем следующую таблицу переходов для автомата без недостижимых состояний:
| A | C | E | G | |
| B | K | E | G | |
| C | J | A | H | |
| E | E | J | H | |
| G | H | A | J | |
| H | G | J | B | |
| J | B | H | G | |
| K | M | E | N | |
| M | J | A | H | |
| N | H | A | J | |
Для нахождения эквивалентных состояний воспользуемся «методом разбиения», который заключается в разбиении множества состояний на непересекающиеся подмножества или блоки, такие, что неэквивалентные состояния попадают в разные блоки. Сначала все состояния разобьем на два блока: допускающих и отвергающих состояний.
Под действием входного символа 0 блок  разбивается на блоки
разбивается на блоки  и
и  , т. к. состояния
, т. к. состояния  ,
,  ,
,  переходят в состояния, принадлежащие первому блоку (а, именно, в состояния
переходят в состояния, принадлежащие первому блоку (а, именно, в состояния  ,
,  ,
,  соответственно), тогда как состояния
соответственно), тогда как состояния  переходят в состояния, принадлежащие второму блоку (а, именно, в состояния
переходят в состояния, принадлежащие второму блоку (а, именно, в состояния  ,
,  ,
,  ,
,  соответственно). Это означает, что для любого состояния из множества
соответственно). Это означает, что для любого состояния из множества  и любого состояния из
и любого состояния из  соответствующие состояния-преемники по входу 0 будут неэквивалентны. Итак, новое разбиение имеет вид
соответствующие состояния-преемники по входу 0 будут неэквивалентны. Итак, новое разбиение имеет вид
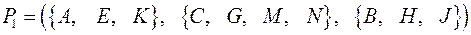 .
.
Разбивая блок  из
из  относительно 0 получаем
относительно 0 получаем
 .
.
Разбивая блок 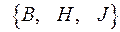 из
из  относительно 0 получаем
относительно 0 получаем
 .
.
Разбивая блок 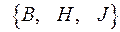 из
из  относительно 0 получаем
относительно 0 получаем
 .
.
 не допускает дальнейшего разбиения. Чтобы убедиться в этом, заметим, что все состояния блока
не допускает дальнейшего разбиения. Чтобы убедиться в этом, заметим, что все состояния блока 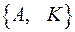 переходят относительно 0 в состояние блока
переходят относительно 0 в состояние блока 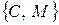 , относительно 1 – в состояние блока
, относительно 1 – в состояние блока  , относительно 2 – в состояние блока
, относительно 2 – в состояние блока  . Аналогично, блок
. Аналогично, блок  переходит в блоки
переходит в блоки 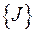 ,
, 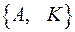 ,
,  относительно 0, 1, 2 соответственно. А блок
относительно 0, 1, 2 соответственно. А блок  переходит в блоки
переходит в блоки  ,
, 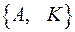 ,
, 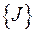 , относительно 0, 1, 2 соответственно. Оставшиеся блоки имеют по одному элементу и поэтому автоматически исключают дальнейшее разбиение.
, относительно 0, 1, 2 соответственно. Оставшиеся блоки имеют по одному элементу и поэтому автоматически исключают дальнейшее разбиение.
Следовательно, состояния  и
и  ,
,  и
и  ,
,  и
и  являются эквивалентными. Объединим каждую пару состояний в одно новое, получим:
являются эквивалентными. Объединим каждую пару состояний в одно новое, получим:  ,
,  ,
,  . Подставляя эти новые имена в автомат и удаляя лишние строки, получим минимальный автомат, эквивалентный исходному:
. Подставляя эти новые имена в автомат и удаляя лишние строки, получим минимальный автомат, эквивалентный исходному:
| X | Y | E | Z | |
| B | X | E | Z | |
| Y | J | X | H | |
| E | E | J | H | |
| Z | H | X | J | |
| H | Z | J | B | |
| J | B | H | Z | |
Индивидуальные задания
Варианты индивидуальных заданий указаны в таблице. Для заданий 1, 4 – 8 указан номер автомата(см. Приложение). Для заданий 2, 3 указаны буквы – пункты задания.
| Вариант | Задания | |||||||
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | |
| 1. | № 1 | г), л) | л), д) | №11 | № 2 | № 7,8 | №16 | №24 |
| 2. | № 2 | б), к) | г), и) | №12 | № 3 | № 8,9 | №17 | №23 |
| 3. | № 3 | в), и) | е), к) | №13 | № 4 | № 9,10 | №18 | №22 |
| 4. | № 4 | г), з) | ж),к) | №14 | № 5 | № 1,10 | №19 | №20 |
| 5. | № 5 | д),ж) | з), ж) | №15 | № 6 | № 1,2 | №20 | №21 |
| 6. | № 6 | е), л) | и),д) | №11 | № 7 | № 2,3 | №21 | №19 |
| 7. | № 7 | ж),к) | и),в) | №12 | № 8 | № 3,4 | №22 | №18 |
| 8. | № 8 | з), ж) | к), з) | №13 | № 9 | № 4,5 | №23 | №17 |
| 9. | № 9 | и),д) | л),в) | №14 | № 10 | № 5,6 | №24 | №16 |
| 10. | № 1 | и),в) | б),к) | №11 | № 2 | № 7,8 | №16 | №23 |
| 11. | № 2 | б),ж) | г), и) | №12 | № 3 | № 8,10 | №17 | №22 |
| 12. | № 3 | л), д) | е), к) | №11 | № 4 | № 9,10 | №18 | №21 |
| 13. | № 4 | г), и) | ж),к) | №14 | № 5 | № 1,9 | №19 | №20 |
| 14. | № 5 | е), к) | з), ж) | №11 | № 6 | № 1,3 | №20 | №19 |
| 15. | № 6 | ж),к) | и),д) | №15 | № 7 | № 2,5 | №21 | №18 |
| 16. | № 7 | з), ж) | и),в) | №12 | № 8 | № 3,64 | №22 | №17 |
| 17. | № 8 | и),д) | г), л) | №13 | № 9 | № 4,7 | №23 | №16 |
| 18. | № 9 | и),в) | б), к) | №14 | № 10 | № 5,8 | №16 | №23 |
| 19. | № 10 | к), з) | в), и) | №15 | № 9 | № 6,9 | №17 | №22 |
| 20. | № 1 | л),в) | г), з) | №11 | № 2 | № 7,10 | №16 | №20 |
| 21. | № 2 | б),к) | д),ж) | №12 | № 3 | № 5,9 | №17 | №21 |
| 22. | № 3 | г), и) | е), л) | №13 | № 4 | № 4,10 | №18 | №22 |
| 23. | № 4 | е), к) | ж),к) | №14 | № 5 | № 3,10 | №19 | №19 |
| 24. | № 5 | ж),к) | з), ж) | №15 | № 6 | № 1,7 | №20 | №16 |
| 25. | № 6 | з), ж) | и),д) | №11 | № 7 | № 2,8 | №21 | №17 |
| 26. | № 7 | и),д) | и),в) | №12 | № 8 | № 3,9 | №22 | №21 |
| 27. | № 8 | и),в) | г), к) | №13 | № 9 | № 4,10 | №23 | №20 |
| 28. | № 9 | к), з) | б), и) | №14 | № 10 | № 2,6 | №18 | №24 |
1. Для заданного автомата найдите:
а) самую короткую цепочку, допускаемую автоматом;
б) три другие цепочки, допускаемых этим автоматом;
в) три цепочки, которые отвергаются этим автоматом.
2. Постройте конечный автомат со входным алфавитом {0, 1}, который допускает в точности следующее множество цепочек:
а) Все входные цепочки.
б) Ни одной входной цепочки.
в) Входную цепочку 101.
г) Две входные цепочки: 01, 0100.
д) Все входные цепочки, кончающиеся на 1 и начинающиеся с 0.
е) Все цепочки, не содержащие ни одной единицы.
ж) Все цепочки, содержащие в точности три единицы.
з) Все цепочки, в которых перед и после каждой единицы стоит 0.
и) Пустую цепочку и 011.
к) Все входные цепочки, кроме пустой и цепочки 11.
л) Цепочки, у которых единицы и нули чередуются.
3. Постройте конечные распознаватели для описанных ниже множеств цепочек из нулей и единиц. Затем превратите каждый распознаватель в процессор с концевым маркером. Наконец сделайте так, чтобы процессор обнаруживал допустимость и недопустимость цепочек как можно скорее.
а) Число единиц четное, а число нулей – нечетное.
б) Между вхождениями единиц четное число нулей.
в) Число вхождений пары 00 нечетное, причем допускаются наложения пар друг на друга.
г) Число вхождений пары 00 четное, причем не допускаются наложения пар друг на друга.
д) Каждый третий символ – единица.
е) Имеется, по крайней мере, одна единица
ж) За каждым вхождением пары 11 следует 0.
з) Перед каждым вхождением пары 11 следует 0.
и) За каждым вхождением пары 11 следует 01.
к) За каждым вхождением пары 01 следует 10.
л) После четного числа вхождения единиц следует четное число нулей, после нечетного числа вхождения единиц – нечетное число нулей.
4. Опишите словами множества цепочек, распознаваемых каждым из следующих автоматов.
5. Для каждого из автоматов найдите входную цепочку или цепочки с минимальной суммарной длиной, такие, что под их действием
а) каждое возможное состояние имеет место хотя бы раз,
б) каждый возможный переход происходит хотя бы раз.
6. Найдите различающую цепочку (если она существует) для следующей пары автоматов.
7. Найдите недостижимые состояния автомата
8. Построить минимальный автомат эквивалентный данному автомату.
Приложение
| А | D | A | А | A | B | А | C | A | А | D | A | А | B | C | |||||||||
| B | A | C | B | A | C | B | A | C | B | A | E | B | A | C | |||||||||
| C | A | F | C | A | F | C | B | F | C | A | D | C | A | F | |||||||||
| D | B | C | D | B | C | D | B | C | D | B | C | D | C | B | |||||||||
| E | B | C | E | B | C | E | B | D | E | B | F | E | B | C | |||||||||
| F | E | A | F | E | D | F | E | A | F | E | A | F | D | E | |||||||||
| №1 | №2 | №3 | №4 | №5 |
| А | D | A | А | B | A | А | D | B | А | D | B | А | B | C | |||||||||
| B | A | C | B | A | C | B | A | C | B | C | E | B | A | E | |||||||||
| C | A | F | C | F | A | C | E | D | C | A | D | C | A | F | |||||||||
| D | B | A | D | B | C | D | B | C | D | B | C | D | B | C | |||||||||
| E | B | C | E | B | C | E | B | F | E | B | F | E | B | C | |||||||||
| F | E | A | F | E | D | F | E | A | F | A | E | F | D | A | |||||||||
| №6 | №7 | №8 | №9 | №10 |
| A | B | A | A | B | C | A | B | A | A | B | C | A | B | C | |||||||||
| B | B | C | B | C | B | B | D | C | B | D | B | B | D | B | |||||||||
| C | C | C | C | C | C | C | C | D | C | C | D | C | C | D | |||||||||
| D | D | D | D | D | D | D | D | D | |||||||||||||||
| №11 | №12 | №13 | №14 | №15 |
| A | C | E | G | A | J | D | I | A | H | E | G | A | I | C | G | ||||||||||
| B | K | E | G | B | J | G | I | B | K | J | G | B | G | E | K | ||||||||||
| C | J | A | H | C | K | A | H | C | J | A | H | C | I | A | H | ||||||||||
| D | F | A | G | D | C | A | I | D | F | A | G | D | F | A | G | ||||||||||
| E | E | J | H | E | G | J | H | E | E | J | H | E | E | I | H | ||||||||||
| F | D | I | A | F | D | F | A | F | D | I | A | F | B | J | A | ||||||||||
| G | H | A | J | G | H | A | J | G | H | A | J | G | H | A | I | ||||||||||
| H | G | J | B | H | I | J | B | H | J | G | B | H | G | I | D | ||||||||||
| I | D | F | G | I | C | E | I | I | F | D | G | I | B | F | G | ||||||||||
| J | B | H | G | J | B | H | I | J | B | H | G | J | D | H | G | ||||||||||
| K | M | E | N | K | J | M | N | K | M | N | G | K | I | M | N | ||||||||||
| M | J | A | H | M | C | A | N | M | J | G | B | M | I | A | H | ||||||||||
| N | H | A | J | N | C | E | I | N | E | J | H | N | H | A | I | ||||||||||
| №16 |
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-06-21 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд
Интересно: