Глава 7. Закон больших чисел. Центральная предельная теорема.
Неравенство Чебышева
Пусть случайная величина x имеет математическое ожидание Мx и дисперсию Dx. Тогда для любого e>0 справедливо неравенство Чебышева:
.
Это неравенство часто используют в виде:
Доказательство этих неравенств основывается на неравенстве Маркова: для любой случайной величины x вероятность события {w: ôxô³e} не превосходит произведения частного 1/e на математическое ожидание модуля случайной величины, то есть Р(ôxô³e)£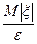 
. Справедливо и неравенство Колмогорова: если x1,x2,…,xn независимые случайные величины имеют конечные дисперсии Dxi, то для любого e>0 справедливо неравенство
.
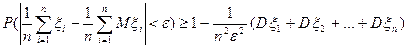Задача 1. В 400 испытаниях Бернулли вероятность успеха в каждом испытании равна 0,8. С помощью неравенства Чебышева оценить вероятность того, что разница междучислом успехов в этих испытаниях и средним числом успехов не превысит 20.
Решение. Число успехов в этих испытаниях распределено по закону Бернулли, поэтому среднее число успехов равно Мx=np=400×0,8=320, а Dx=npq=400×0,8×0,2=64. Тогда в силу неравенства Чебышева имеем:
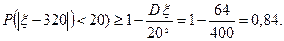
Вычислим эту же вероятность с помощью приближенной (интегральной) формулы Муавра-Лапласа (см. главу 4):
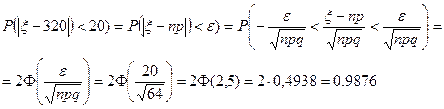
Последнее вычисление показывает, что неравенство Чебышева дает довольно грубые оценки вероятностей.
Закон больших чисел
Пусть задана бесконечная последовательность независимых одинаково распределенных случайных величин 
, для которых существуют математическое ожидание 
и дисперсия 
. Тогда для любого e>0
.
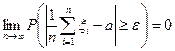Суть закона больших чисел состоит в том, что при возрастании числа слагаемых (т.е. одинаково распределенных случайных величин) среднее арифметическое этих слагаемых мало отличается от математического ожидания 
. Любое отклонение среднего арифметического случайных величин от числа при достаточно большом числе слагаемых – маловероятно.
Например. Пусть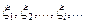 
– последовательность случайных величин, каждая из которых равна числу успехов в одном испытании Бернулли (т.е. 1 в случае успеха и 0 – в случае неудачи). Закон распределения каждой такой случайной величины имеет вид:
| xi | ||
| P | q | P |
Здесь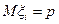 
и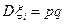 
. Тогда среднее арифметическое 
равно частоте успехов в n испытаниях, и закон больших чисел утверждает, что эта частота успехов стремится к вероятности успеха p, если число слагаемых (т.е. число испытаний) стремится к бесконечности.
Центральная предельная теорема (ЦПТ)
Если 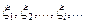— независимые одинаково распределенные случайные величины, такие, что и 
, i = 1, 2,..., то для любого вещественного х
,
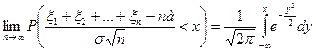Смысл центральной предельной теоремы заключается в том, что сумма 
случайных величин при надлежащем «центрировании» и «нормировании» и при увеличении числа слагаемых (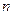
®¥) ведет себя почти как стандартно распределенная случайная величина. (Напомним, что x называется стандартно распределенной, если 
.)
Например. Пусть 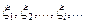– последовательность случайных величин, удовлетворяющая условиям предыдущего примера. В этом случае сумма 
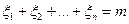есть число успехов в 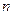испытаниях Бернулли. Из ЦПТ следует, что
,
где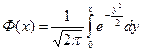 
– функция Лапласа.
Тогда вероятность того, что число успехов будет заключено между 
и 
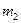равна
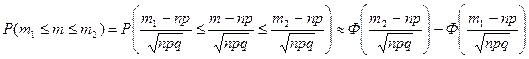
Этот результат называется интегральной теоремой Муавра–Лапласа и используется при npq<9. Если р£1 и npq £ 9, для биномиального распределения используют пуассоновское приближение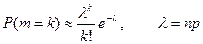 
, основанное на формуле Пуассона при р®0, n®¥, np®l.
Задача 2. В продукции цеха детали отличного качества составляют 50%. Детали укладываются в коробки по 200 шт. в каждой. Какова вероятность того, что число деталей отличного качества в коробке отличаться от 100 не более, чем на 5?
Решение. Пусть xn - случайное число деталей отличного качества в коробке, тогда при n=200,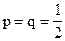 
получим: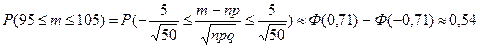 
Задача 3. Используя условия предыдущей задачи, указать в каких границах с вероятностью 0,997 находится число деталей отличного качества в коробке.
Решение. По таблицам при условии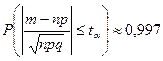 
находим ta и следовательно, Sn лежит в пределах 
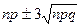, т.е. число деталей отличного качества в коробке с вероятностью 0,997 находится в пределах 100 ± 21.
Задача 4. Используя условия примера 1, определить, сколько деталей надо положить в коробку, чтобы с вероятностью, не меньшей 0,99, можно было утверждать, что число деталей отличного качества в коробке не меньше 100.
Решение. Необходимо найти n из условия Р (Sn³ 100)³ 0,99. Используя нормальное приближение, получаем
,
и из таблиц получаем неравенство 
откуда, полагая 
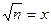, при 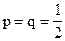имеем х2-2,3х-200³0, откуда получаем n³240.
Задача 5. Известно, что процент брака для некоторой детали равен 0,5%. Контролер проверяет 1000 деталей. Какова вероятность обнаружить ровно 3 бракованных детали? Какова вероятность обнаружить не меньше 3-х бракованных деталей?
Решение. Имеем 1000 испытаний Бернулли с вероятностью р=0,005 «успеха», здесь npq<5. Применяя пуассоновское приближение с l = np = 5, получаем
и по таблицам находим: P(m1000 =3) » 0,14, Р(m1000<3)» 0,875.
Задача 8. Телефонная станция обслуживает 2000 абонентов, в час пик каждый абонент использует связь в среднем в течение 2 минут, т.е. мы считаем, что абонент с вероятностью 
использует связь. Какое наименьшее число линий необходимо, чтобы только один из 100 вызовов получал отказ?
Решение. Считая вызовы абонентов независимым, имеем 2000 испытаний Бернулли с вероятностью "успеха" р=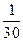 
. Надо найти число линий N из условия
Р(m2000³N) £0,01. Применяя приближение Пуассона с 
, по таблицам находим N»87. При использовании нормального приближения получается, что достаточно 86 линий.