Математи́ческая стати́стика — наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов.
поиску
Во многих своих разделах математическая статистика опирается на теорию вероятностей, дающую возможность оценить надёжность и точность выводов, делаемых на основании ограниченного статистического материала.
Пример 1
Студенческая группа сдала коллоквиум по матанализу со следующими результатами:
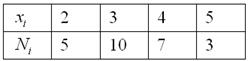
Требуется определить среднюю успеваемость группы
Как нетрудно понять, роль вариант 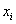 здесь играют полученные оценки, а
здесь играют полученные оценки, а 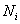 – это соответствующие частоты – количество студентов, которые получили ту или иную оценку. Подсчитаем общую численность группы:
– это соответствующие частоты – количество студентов, которые получили ту или иную оценку. Подсчитаем общую численность группы:
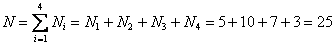 человек и, привыкаем к терминам, исследуемое множество называют статистической или генеральной совокупностью, а количество его элементов – объёмом совокупности.
человек и, привыкаем к терминам, исследуемое множество называют статистической или генеральной совокупностью, а количество его элементов – объёмом совокупности.
Теперь обратим внимание на следующую вещь: двоечников и отличников у нас мало, а нормальных студентов:) много. И возникает вопрос: как вычислить «справедливую» среднюю оценку по всей совокупности? Решение напрашивается – с помощью так называемой средневзвешенной средней:
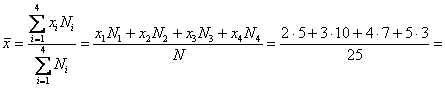
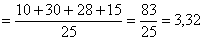 – средняя успеваемость по группе.
– средняя успеваемость по группе.
В примере исследуется ВСЯ совокупность, все студенты, и поэтому её называют генеральной совокупностью, а соответствующее среднее значение – генеральной средней. Но такая ситуация редкость. Редко когда удаётся исследовать всю совокупность.
И сейчас мы подошли к основному методу математической статистики:
Задача
Федор пошёл на базу исследовать помидоры. Требуется определить среднюю массу помидора и среднюю долю первосортных помидоров.
Разбираемся в ситуации. Очевидно, что на базе находится очень и очень много помидоров, обозначим их общее количество через 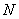 . Это генеральная совокупность. Для того чтобы решить задачу, можно взвесить каждый овощ:
. Это генеральная совокупность. Для того чтобы решить задачу, можно взвесить каждый овощ: 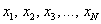 (в граммах, например) и вычислить генеральную среднюю:
(в граммах, например) и вычислить генеральную среднюю:
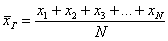 – среднюю массу помидора.
– среднюю массу помидора.
Но это долго и трудно, даже если Феде будут помогать все его однокурсники.
Поэтому для оценки параметров генеральной совокупности целесообразно использовать выборочный метод. Его суть состоит в том, что из генеральной совокупности достаточно выбрать 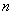 объектов, которые хорошо характеризуют всю совокупность. Это «хорошо» называют представительностью или, как говорят, репрезентативностью выборки. Проговорим это модное слово вслух: ре-пре-зен-та-тив-ность.
объектов, которые хорошо характеризуют всю совокупность. Это «хорошо» называют представительностью или, как говорят, репрезентативностью выборки. Проговорим это модное слово вслух: ре-пре-зен-та-тив-ность.
Что нужно для того, чтобы обеспечить репрезентативность?
Ну, во-первых, выборка должна быть достаточно велика, помидоров так 500-1000 точно, что уже вполне по силам даже одному Феде.
Примечание: в дальнейшем мы сформулируем более строгие статистические критерии на счёт оптимального размера выборки.
Во-вторых, отбор следует осуществлять равномерно – из каждого ящика.
В-третьих, отбор должен быть случайным. Для этого используются разные приёмы, и самый простой здесь – это выбор «вслепую» из случайно выбранного места ящика, обязательно с разной глубины (а то мало ли, что поставщик там мог спрятать).
И, в-четвёртых (а может быть, и, в-первых), есть и другие факторы, которые могут быть менее очевидны. В частности, важно знать, а однородна ли генеральная совокупность? Так, если помидоры поступили от разных поставщиков, то каждую партию полезно исследовать по отдельности (сделать несколько выборок).
Итак, пусть Фёдор по всем правилам выбрал 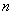 помидоров, и теперь дело за малым – взвесить каждый овощ:
помидоров, и теперь дело за малым – взвесить каждый овощ: 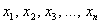 (граммы) и вычислить выборочную среднюю:
(граммы) и вычислить выборочную среднюю:
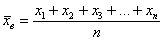 – среднюю массу помидора в выборке.
– среднюю массу помидора в выборке.
При этом очевидно, что чем больше объем 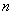 выборочной совокупности, тем полученное значение будет точнее приближать генеральную среднюю
выборочной совокупности, тем полученное значение будет точнее приближать генеральную среднюю 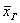 .
.
Но фишка состоит в том, что если начать увеличивать выборку в два, три и бОльшее количество раз, то будут получаться выборочные средние, которые мало отличаются от уже рассчитанного значения 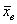 . Вы спрОсите, как это установлено? Эмпирически. В результате огромного количества реально проведённых исследований.
. Вы спрОсите, как это установлено? Эмпирически. В результате огромного количества реально проведённых исследований.
Таким образом, нет никакого практического смысла тратить силы, время, деньги, нервы на исследование бОльшей выборки и тем более, всей генеральной совокупности.
Вот оно как – в статистике есть и прямая экономическая выгода!
И ещё один момент, чуть не забыл: обратите внимание на используемые буквы – они стандартны. Другие варианты встречаются реже.
Вторая часть задачи. Определим вместе с Фёдором среднюю долю высококачественных помидоров на базе (ну мы же не садисты заставлять его одного заново перебирать 1000 штук:)).
В отличие от первого этапа, здесь мы исследуем уже качественный признак, для которого, тем не менее, можно сформулировать чёткие критерии. Пусть первосортный помидор – это чёрный, лысый красный, спелый, без видимых дефектов, массой выше среднего.
Совершенно понятно, что генеральная совокупность содержит 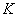 таких помидоров, и существует точное значение:
таких помидоров, и существует точное значение:
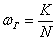 – генеральная доля первосортных помидоров.
– генеральная доля первосортных помидоров.
Но по причине трудозатратности и нецелесообразности полного исследования, достаточно подсчитать количество 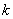 таких овощей в выборке и вычислить:
таких овощей в выборке и вычислить:
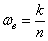 – выборочную долю, которая будет весьма близка к истинному значению
– выборочную долю, которая будет весьма близка к истинному значению 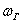 . Но это только, напомню, при условии грамотно организованной и проведённой выборки.
. Но это только, напомню, при условии грамотно организованной и проведённой выборки.
Доля, как вы догадываетесь, может принимать значение от 0 до 1, и иногда её домножают на 100, чтобы выразить этот показатель в процентах.
Готово.
Пример 2
а) Урожайность картофеля по трём областям за **** год составила 147, 145, 155 ц/га (центнеров с га). Требуется вычислить среднюю урожайность.
Метрическая справка: 1 центнер = 100 кг, 1 тонна = 1000 кг;
1 гектар (га) = 10000 квадратных метров;
показатель ц/га обозначает, сколько центнеров собрано с 1 гектара.
Не забываем приписывать к итоговому результату размерность! (секунды, граммы и т.д., а в данном случае – ц/га).
Вариация чуть сложнее:
б) Известны следующие данные по трём областям:

Требуется вычислить среднюю урожайность.
Обратите внимание, что здесь урожайность, скажем, по 3-й области велика, но её посевная площадь мала. Поэтому урожайность уместно «взвесить» по площадям.
и третий пункт, творческий:
в) вычислить среднюю урожайность по следующим данным:

«Валовой» – это значит, всего собрано по области.
Решения и ответы:
Пример 2
а) Используем простую среднюю:
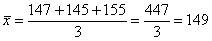 ц/га – в среднем по трём областям.
ц/га – в среднем по трём областям.
б) Используем средневзвешенную (по площади) среднюю:
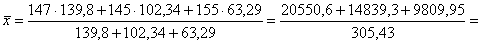
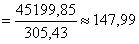 ц/га в среднем по трём областям.
ц/га в среднем по трём областям.
в) Здесь урожайность тоже следует переоценить через посевную площадь, используя формулу Посевная площадь = Валовой сбор / Урожайность:
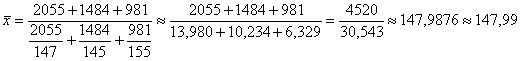 ц/га в среднем по трём областям. Такой вид средней иногда называют средней гармонической.
ц/га в среднем по трём областям. Такой вид средней иногда называют средней гармонической.
2. Дискретный вариационный ряд.
Полигон частот и эмпирическая функция распределения
Дискретный вариационный ряд – это упорядоченное по возрастанию (как правило) множество вариант 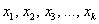 (значений величины
(значений величины 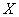 ) и соответствующих им частот либо относительных частот.
) и соответствующих им частот либо относительных частот.
Частоты выборочной совокупности обозначают через 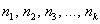 , частоты генеральной совокупности – через
, частоты генеральной совокупности – через 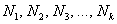 . И сразу разбираемся с новым термином.
. И сразу разбираемся с новым термином.
Относительные частоты рассчитываются по формулам:
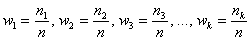 , где
, где 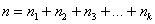 – объем выборки, при этом, сумма всех относительных частот:
– объем выборки, при этом, сумма всех относительных частот: 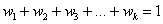 .
.
Аналогично для совокупности генеральной:
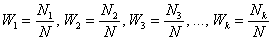 , где
, где 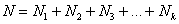 – её объем, и, очевидно:
– её объем, и, очевидно: 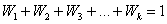
И тут вспоминается Пример 1 об оценках по матанализу в группе из 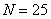 студентов:
студентов:

– пожалуйста, пример дискретного вариационного ряда, где варианты 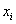 – это оценки, а частоты
– это оценки, а частоты 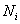 – количество студентов, получивших ту или иную оценку.
– количество студентов, получивших ту или иную оценку.
Для разминки найдём относительные частоты:

и непременно проконтролируем, что: 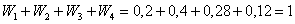 .
.
Все вычисления обычно проводят на калькуляторе либо в Экселе, а результаты заносят в таблицу, при этом, в статистике данные чаще располагают не в строках, а в столбцах:
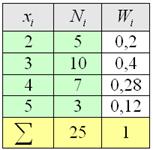
Такое расположение обусловлено тем, что количество вариант может быть достаточно велико, и они просто не вместятся в строчку. Не редкость, когда их 10-20, а бывает, и 100-200.
Пример 2
По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3. Требуется:
– составить вариационный ряд и построить полигон частот;
– найти относительные частоты и построить эмпирическую функцию распределения.
Решение: в условии прямо сказано о том, что перед нами выборка из генеральной совокупности (всех рабочих цеха), и первое, что логично сделать – подсчитать её объем, т.е. количество рабочих. В данном случае это легко сделать устно: 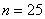 .
.
Квалификационные разряды – есть величина дискретная, и поэтому нам предстоит составить дискретный вариационный ряд (обратите внимание, что в условии ничего не сказано о характере ряда).
Как это сделать?
Если у вас под рукой нет вычислительных программ, то вручную. При этом оптимальным может быть следующий алгоритм: сначала окидываем взглядом все числа и определяем среди них минимальное (примерно) и максимальное (примерно). В данном случае ориентировочный диапазон – от 1 до 7. Записываем их в столбец на черновике и обводим в кружочки. Далее начинаем вычёркивать карандашом числа из исходного списка:
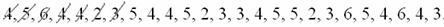
и делать около соответствующих кружков засечки:

После того, как все числа будут вычеркнуты, подсчитываем количество засечек в каждой строке:
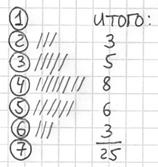
И обязательно проверяем, получается ли у нас в сумме объём выборки 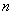 :
:
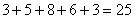 , отлично, искомый ряд составлен, заносим полученные значения в таблицу на чистовик:
, отлично, искомый ряд составлен, заносим полученные значения в таблицу на чистовик:

…ну что же, вполне и вполне логично – рабочих средней квалификации много, а учеников и мастеров – мало. Полученные результаты позволяют достаточно точно судить об уровне квалификации всего цеха (если, конечно, выборка представительна)
Построенный вариационный ряд также называют статистическим распределением выборки, причём, этот термин применим не только для дискретного, но и для интервального ряда, который мы рассмотрим ниже.
Построим полигон частот. Это статистический аналог многоугольника распределения дискретной случайной величины. Полигон частот – это ломаная, соединяющая соседние точки
 :
:
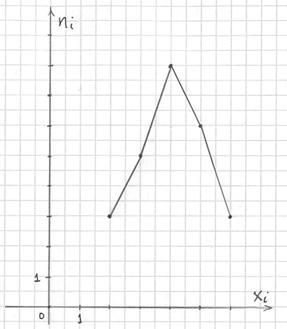
Вторая часть задачи. Найдём относительные частоты 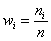 , для этого каждую частоту
, для этого каждую частоту 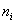 делим на
делим на 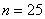 и результат заносим в дополнительный столбец, далее я перехожу к электронной версии:
и результат заносим в дополнительный столбец, далее я перехожу к электронной версии:
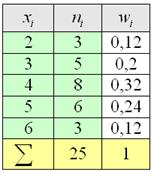
– обязательно проверяем, что сумма относительных частот равна единице!
Иногда требуется построить полигон относительных частот. Как вы правильно догадываетесь – это ломаная, соединяющая соседние точки 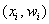 . Но такое задание больше характерно для интервального вариационного ряда.
. Но такое задание больше характерно для интервального вариационного ряда.
А теперь посмотрим на относительные частоты и задумаемся, на что они похожи? …Правильно, на вероятности. Так, например, можно сказать, что 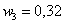 – есть примерная вероятность того, что наугад выбранный рабочий цеха будет иметь 4 разряд. «Примерная» – по той причине, что перед нами выборка.
– есть примерная вероятность того, что наугад выбранный рабочий цеха будет иметь 4 разряд. «Примерная» – по той причине, что перед нами выборка.
А вот если учесть ВСЕХ рабочих цеха (всю генеральную совокупность), то рассчитанные относительные частоты 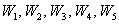 – и есть в точности эти вероятности.
– и есть в точности эти вероятности.
Построим эмпирическую функцию распределения 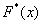 . Это статистический аналог функции распределения из тервера. Данная функция определяется, как отношение:
. Это статистический аналог функции распределения из тервера. Данная функция определяется, как отношение:
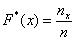 , где
, где 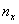 – количество вариант СТРОГО МЕНЬШИХ, чем
– количество вариант СТРОГО МЕНЬШИХ, чем  ,
,
при этом «икс» «пробегает» все значения от «минус» до «плюс» бесконечности.
И процесс пошёл:
Очевидно, что на интервале 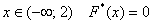 , и, кроме того, функция равна нулю ещё и в точке
, и, кроме того, функция равна нулю ещё и в точке 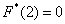 . Почему? Потому, что значение
. Почему? Потому, что значение 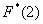 определяет количество вариант, которые СТРОГО меньше двух, а это количество равно нулю.
определяет количество вариант, которые СТРОГО меньше двух, а это количество равно нулю.
На промежутке 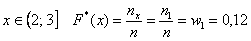 – и опять обратите внимание, что значение
– и опять обратите внимание, что значение  не учитывает рабочих 3-го разряда, т.к. речь идёт о вариантах, которые СТРОГО меньше трёх.
не учитывает рабочих 3-го разряда, т.к. речь идёт о вариантах, которые СТРОГО меньше трёх.
На промежутке 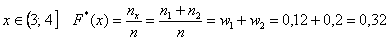 и далее процесс продолжается по принципу накопления частот:
и далее процесс продолжается по принципу накопления частот:
– если 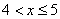 , то
, то 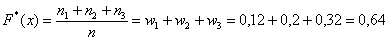 ;
;
– если 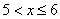 , то
, то 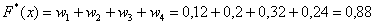 ;
;
– и, наконец, если 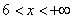 , то
, то 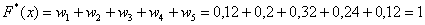 – и в самом деле, для ЛЮБОГО «икс» из интервала
– и в самом деле, для ЛЮБОГО «икс» из интервала 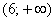 ВСЕ частоты расположены СТРОГО левее этого «икс».
ВСЕ частоты расположены СТРОГО левее этого «икс».
Накопленные относительные частоты удобно записывать в отдельный столбец таблицы, при этом алгоритм вычислений очень прост: сначала сносим слева 1-е значение (красная стрелка), а каждое следующее получаем как сумму предыдущего и относительной частоты из текущего левого столбца (зелёные обозначения):
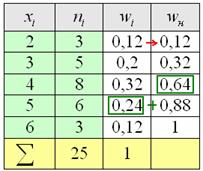
Вот, кстати, ещё один довод за вертикальную ориентацию данных – справа по надобности можно приписывать дополнительные столбцы.
Саму функцию принято записывать в кусочном виде:

а её график представляет собой ступенчатую фигуру:
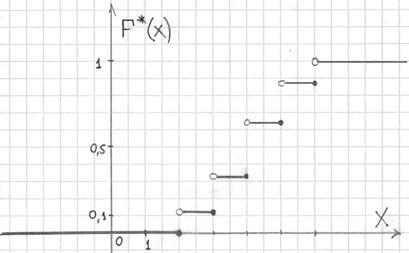
Эмпирическая функция распределения не убывает и принимает значения из промежутка 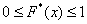 , и если у вас вдруг получится не так, то ищите ошибку.
, и если у вас вдруг получится не так, то ищите ошибку.
Домашнее задание 1
Дано статистическое распределение выборки
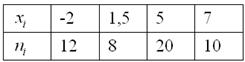
Составить эмпирическую функцию распределения, выполнить чертёж
3. Интервальный вариационный ряд.
Гистограмма относительных частот
Пример 3
По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные (в некоторых денежных единицах):
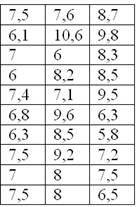
Требуется составить вариационный ряд распределения, построить гистограмму и полигон относительных частот + бонус – эмпирическую функцию распределения.
Очевидно, что перед нами выборочная совокупность объемом 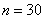 наблюдений и вопрос номер один: какой ряд составлять – дискретный или интервальный? Смотрим на таблицу: среди предложенных цен есть одинаковые, но их разброс довольно велик, и поэтому здесь целесообразно провести интервальное разбиение. К тому же цены могут быть округлёнными.
наблюдений и вопрос номер один: какой ряд составлять – дискретный или интервальный? Смотрим на таблицу: среди предложенных цен есть одинаковые, но их разброс довольно велик, и поэтому здесь целесообразно провести интервальное разбиение. К тому же цены могут быть округлёнными.
Тактика действий похожа на исследование дискретного вариационного ряда. Сначала окидываем взглядом предложенные числа и определяем примерный интервал, в который вписываются эти значения. «Навскидку» все значения заключены в пределах от 5 до 11. Далее делим этот интервал на удобные подынтервалы, в данном случае напрашиваются промежутки единичной длины. Записываем их на черновик:
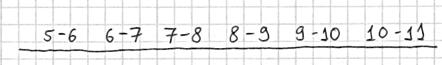
Теперь начинаем вычёркивать числа из исходного списка и записывать их в соответствующие колонки нашей импровизированной таблицы:
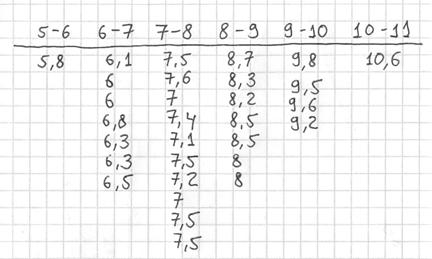
После этого находим самое маленькое число в левой колонке и самое большое значение – в правой. Тут даже ничего искать не пришлось, честное слово, не нарочно получилось:)
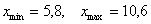 ден. ед. – хорошим тоном считается указывать размерность.
ден. ед. – хорошим тоном считается указывать размерность.
Вычислим размах вариации:
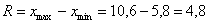 ден. ед. – длина общего интервала, в пределах которого варьируется цена.
ден. ед. – длина общего интервала, в пределах которого варьируется цена.
Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на этот счёт существует формула Стерджеса:
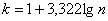 , где
, где 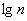 – десятичный логарифм* от объёма выборки и
– десятичный логарифм* от объёма выборки и 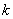 – оптимальное количество интервалов, при этом результат округляют до ближайшего левого целого значения.
– оптимальное количество интервалов, при этом результат округляют до ближайшего левого целого значения.
* есть на любом более или менее приличном калькуляторе
В нашем случае получаем:
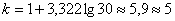 интервалов.
интервалов.
Следует отметить, что правило Стерджеса носит рекомендательный, но не обязательный характер. Нередко в условии задачи прямо сказано, на какое количество интервалов нужно проводить разбиение (на 4, 5, 6, 10 и т.д.), и тогда следует придерживаться именно этого указания.
Длины частичных интервалов могут быть различны, но в большинстве случаев использует равноинтервальную группировку:
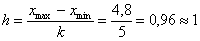 – длина частичного интервала. В принципе, здесь можно было не округлять и использовать длину 0,96, но удобнее, ясен день, 1.
– длина частичного интервала. В принципе, здесь можно было не округлять и использовать длину 0,96, но удобнее, ясен день, 1.
И коль скоро мы прибавили 0,04, то по 5 частичным интервалам у нас получается «перебор»: 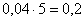 . Посему от самой малой варианты
. Посему от самой малой варианты  отмеряем влево 0,1 влево (половину «перебора») и к значению 5,7 начинаем прибавлять по
отмеряем влево 0,1 влево (половину «перебора») и к значению 5,7 начинаем прибавлять по 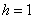 , получая тем самым частичные интервалы. При этом сразу рассчитываем их середины
, получая тем самым частичные интервалы. При этом сразу рассчитываем их середины 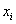 (например,
(например, 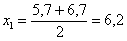 ) – они требуются почти во всех тематических задачах:
) – они требуются почти во всех тематических задачах:
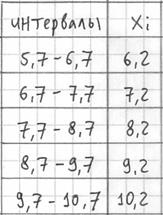
– убеждаемся в том, что самая большая варианта 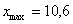 вписалась в последний частичный интервал и отстоит от его правого конца на 0,1.
вписалась в последний частичный интервал и отстоит от его правого конца на 0,1.
Далее подсчитываем частоты по каждому интервалу. Для этого в черновой «таблице» обводим значения, попавшие в тот или иной интервал, подсчитываем их количество и вычёркиваем:
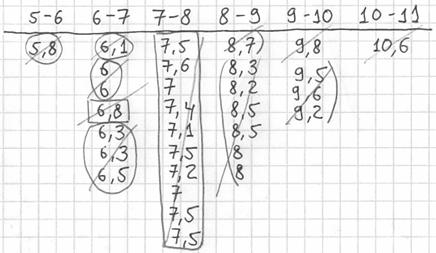
Так, значения из 1-го интервала я обвёл овалами (7 штук) и вычеркнул, значения из 2-го интервала – прямоугольниками (11 штук) и вычеркнул и так далее.
Правило: если варианта попадает на «стык» интервалов, то её следует относить в правый интервал. У нас такая варианта встретилась одна: 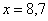 – и её нужно причислить к интервалу
– и её нужно причислить к интервалу 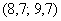 .
.
В результате получаем интервальный вариационный ряд, при этом обязательно убеждаемся в том, что ничего не потеряно: 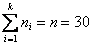 , и, кроме того, рассчитываем относительные частоты
, и, кроме того, рассчитываем относительные частоты 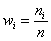 по каждому интервалу, которые уместно округлить до двух знаков после запятой:
по каждому интервалу, которые уместно округлить до двух знаков после запятой:
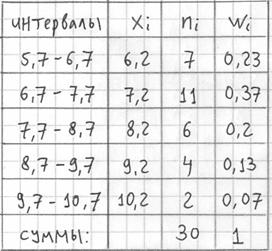
Гистограмма относительных частот – это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов h, а высота – соответствующим относительным частотам,делённым на h::
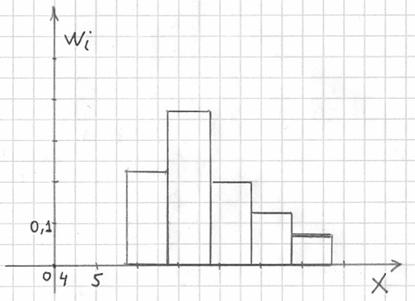
При этом вполне допустимо использовать нестандартную шкалу по оси абсцисс, в данном случае я начал нумерацию с четырёх.
Площадь гистограммы равна единице, и это статистический аналог функции плотности распределения непрерывной случайной величины. Построенный чертёж даёт наглядное и весьма точное представление о распределении цен на ботинки по всей генеральной совокупности. Но это при условии, что выборка представительна.
Вместе с гистограммой нередко требуют построить полигон. Без проблем, полигон относительных частот – это ломаная, соединяющая соседние точки 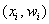 , где
, где 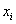 – середины интервалов:
– середины интервалов:
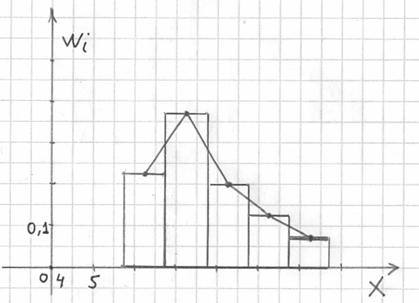
Эмпирическая функция распределения.
Она определяется точно так же, как в дискретном случае:
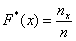 , где
, где 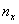 – количество вариант СТРОГО МЕНЬШИХ, чем «икс», который «пробегает» все значения от «минус» до «плюс» бесконечности.
– количество вариант СТРОГО МЕНЬШИХ, чем «икс», который «пробегает» все значения от «минус» до «плюс» бесконечности.
Но вот построить её для интервального ряда намного проще. Находим накопленные относительные частоты:
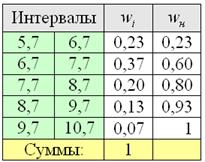
И строим кусочно-ломаную линию, с промежуточными точками 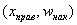 , где
, где 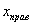 – правые концы интервалов, а
– правые концы интервалов, а 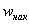 – относительная частота, которая успела накопиться на всех «пройденных» интервалах:
– относительная частота, которая успела накопиться на всех «пройденных» интервалах:
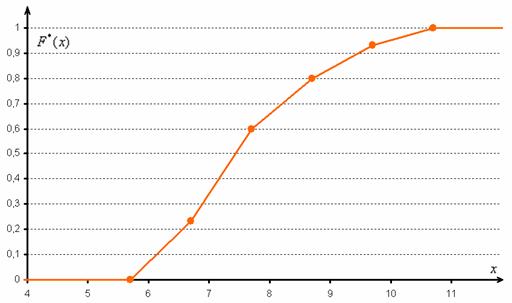
При этом 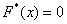 если
если 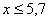 и
и 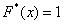 если
если  .
.
Напоминаю, что данная функция не убывает, принимает значения из промежутка 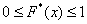 и, кроме того, для ИВР она ещё и непрерывна.
и, кроме того, для ИВР она ещё и непрерывна.
Что ещё важного по теме? Время от времени встречаются таблицы с открытыми крайними интервалами, например:
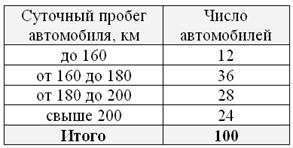
В таких случаях, что убийственно логично, интервалы «закрывают». Обычно поступают так: сначала смотрим на средние интервалы и выясняем длину частичного интервала: 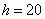 км. И для дальнейшего решения можно считать, что крайние интервалы имеют такую же длину: от 140 до 160 и от 200 до 220 км. Тоже логично.
км. И для дальнейшего решения можно считать, что крайние интервалы имеют такую же длину: от 140 до 160 и от 200 до 220 км. Тоже логично.
Домашнее задание 1
Дано статистическое распределение выборки

Составить эмпирическую функцию распределения, выполнить чертёж
Домашнее задание 2
Выборочная проверка партии чая, поступившего в торговую сеть, дала следующие результаты:

Требуется построить гистограмму и полигон относительных частот, эмпирическую функцию распределения.