«Хабаровская государственная академия экономики и права»
Кафедра математики и математических методов в экономике
П. Я. Бушин
Эконометрика
Анализ временных рядов
Хабаровск 2013
УДК 519.95
ББК В 1
Б 94
Бушин П. Я. Эконометрика. Анализ временных рядов.: учеб. пособие / П. Я. Бушин. – Хабаровск: РИЦ ХГАЭП, 2013. – 96 с.
Содержание учебного пособия в основном соответствует требованиям государственных образовательных стандартов высшего профессионального образования по направлению подготовки «Экономика» квалификации (степень) «бакалавр» очной формы обучения и программой дисциплины «Эконометрика».
В учебном пособии изложены теоретические положения анализа временных рядов – важнейшего раздела курса эконометрики. Приведены разнообразные методы анализа временных рядов как одномерных, так и многомерных, как стационарных, так и нестационарных, приведены методы диагностики рядов на стационарность с помощью различных статистических тестов.
В пособии уделено достаточное внимание как традиционным методам анализа временных рядов, так и современным, таким, как теория коинтеграции, векторная авторегрессия, а также модели коррекции ошибок. Кроме того, изложены начальные методы анализа панельных данных.
Каждый раздел пособия сопровождается рассмотрением практических примеров из экономики. В процессе их рассмотрения используются различные пакеты программ эконометрического анализа
Пособие предназначено для обучающихся по направлению «Экономика», кроме того, оно может быть использовано и магистрантами разных направлений обучения и специалистами, принимающими участие в выработке управленческих решений на основе анализа временных рядов.
Рецензенты:
Р. В. Намм, доктор физ.-мат.наук, профессор, гл. научный сотрудник ВЦ ДВО РАН
В. А. Кузнецов, канд.физ.-мат.наук, доцент кафедры ММиИТ ДВИ-филиал РАНХиГС
Утверждено издательско-библиотечным советом академии в качестве учебного пособия
Бушин П. Я., 2013
Хабаровская государственная академия экономики и права, 2013
Предисловие
Работа современного специалиста в области экономического анализа невозможна без постоянного совершенствования в области экономических знаний, без чтения современной экономической литературы, без обсуждения проблем экономики на различных уровнях принятия решений. А это предполагает знания количественных методов анализа экономической информации, в том числе методами анализа временных рядов, являющихся одним из основных разделов эконометрики.
Эконометрика разрабатывает и использует методы количественного анализа взаимосвязей в социально-экономических процессах и явлениях на основе эмпирической экономической информации с помощью математико-статистических методов и моделей.
Исследование и теоретическое обобщение эмпирических зависимостей в экономической практике, построение моделей анализа и прогноза экономических процессов является центральной проблемой эконометрики, в том числе с использованием методов анализа временных рядов.
Построение эконометрических моделей анализа временных рядов и их использование для анализа и прогнозирования конкретных экономических процессов и явлений немыслимо без использования современных эконометрических пакетов. В учебном пособии уделяется большое внимание использованию пакетов программ для решения прикладных эконометрических проблем.
Все рассмотренные в учебном пособии методы анализа временных рядов проиллюстрированы разнообразными практическими примерами решения тех или иных проблем из области принятия решений, возникающих при использовании эконометрических методов анализа временных рядов. Анализируемая в пособии экономическая информация либо была взята из эконометрической литературы, либо сгенерирована с помощью процедур эконометрического пакета «EViews».
Учебное пособие предназначено для обучающихся по направлению «Экономика» квалификации (степень) Бакалавра очной и заочной форм обучения, а также может быть полезным обучающимся по программе магистратуры и специалитета и специалистам, для которых важно владения методами, необходимыми для выполнения, понимания и оценивания эмпирических исследований.
Основные понятия
Под временным рядом понимается ряд наблюдений, произведённых в последовательные равные промежутки времени, за значениями анализируемой случайной величины. Отдельные такие наблюдения называются уровнями ряда, которые в дальнейшем будем обозначать yt (t = 1,2,…,n), где n – число уровней.
Анализ одномерных временных рядов – это раздел эконометрики, основной идеей которого является попытка представить текущие значения анализируемой переменной и предсказать будущие значения только на основе прошлых значений самой этой переменной и случайных ошибок. Как известно, при рассмотрении моделей пространственной информации (информации, зафиксированной в конкретный момент времени по нескольким показателям для нескольких объектов) предполагается, что заранее установлена причинно-следственная связь между изучаемыми переменными и изменение значений результирующей переменной можно объяснить за счёт изменения значений одной или нескольких других объясняющих переменных. Т.е. предполагается, что исследуемую переменную определяют ряд значимых факторов и что есть возможность идентифицировать эти факторы и учесть влияние каждого из них на эндогенный показатель.
Анализ одномерных временных рядов базируется на другой идее: а именно, значения анализируемой переменной складываются под влиянием большого числа факторов, многие из которых не поддаются идентификации и непосредственному наблюдению и измерению. Поэтому лучшим источником информации о совокупном влиянии всех этих факторов являются значения самой исследуемой переменной в прошлые моменты времени, а также текущие и прошлые значения случайных отклонений и ошибок.
Методы анализа временных рядов представляют собой специальные статистические методы и зависят от типа решаемых задач. При рассмотрении одномерного временного ряда обычно предполагается, что уровни элементов временного ряда не являются выборкой из одинаково распределённой генеральной совокупности и между ними существует взаимозависимость. Поэтому одним из важных методов анализа временных рядов является анализ автоковариаций и автокорреляций, т.е. зависимостей между уровнями элементов одного и того же ряда. Кроме того, методы анализа временных рядов различаются между собой в зависимости от того, является ли временной ряд стационарным или нестационарным.
В самом общем случае можно выделить следующие основные этапы анализа временных рядов.
1. Графическое представление и описание поведения временного ряда.
2. Выделение и удаление неслучайных (детерминированных) составляющих временного ряда.
3. Сглаживание и фильтрация (удаление низко- или высокочастотных составляющих временного ряда).
4. Исследование случайной составляющей временного ряда, построение и проверка адекватности математической модели для её описания.
5. Прогнозирование развития изучаемого процесса на основе имеющегося временного ряда.
6. Исследование взаимосвязи между различными временными рядами.
Глава 1. Анализ одномерных временных рядов
1.1. Анализ временного ряда на стационарность (автокорреляционная функция)
Будем считать ряд стационарным, если его основные числовые характеристики (математическое ожидание, дисперсия и автоковариации) не зависят от времени.
Одним из основных свойств уровней элементов временного ряда является наличие между ними зависимостей, которые измеряются коэффициентами автоковариации и автокорреляции. Автоковариацией называется ковариация, измеренная для уровней элементов одного и того же временного ряда, отстоящих друг от друга на определённый временной интервал, называемый лагом. Величину автоковариации порядка s (на лаге s) будем обозначать через γts. Определяется она соотношением:
γts = M ((yt-µt)(yt+s -µt+s)),
где М (yt) = µt – математическое ожидание yt.
При s = 0 получаем дисперсию переменной y t, т.е.
M ((yt-µt)2) = γt0 = σt2.
Для стационарного временного ряда все эти три характеристики не зависят от времени:
М (yt) = µ,
M ((yt-µ)(yt+s -µ)) = γs,(зависит только от величины лага s),
γ0 = M (yt-µ)2 = σ2 < ∞.
Вместо автоковариации иногда удобнее иметь дело с автокорреляцией, определяемой из соотношения
γs/γ0, (s=0,1,2….).
Автокорреляция порядка s определяется как коэффициенты парной корреляции между уровнями элементов одного и того же временного ряда, сдвинутых относительно друг друга на определённый период времени s. Выборочный коэффициент автокорреляции порядка s будем обозначать через rs, и одна из формул по его вычислению выглядит следующим образом:
.
Введём понятие «белого шума». Это стационарный случайный процесс, имеющий нулевое математическое ожидание, постоянную (конечную, ненулевую) дисперсию и нулевую автоковариацию для любого лага. Нулевая автоковариация на любом лаге означает, что соответствующие наблюдения в этом процессе не коррелированы (отсутствие автокорреляции любого порядка). В качестве примера белого шума можно привести остатки классической регрессионной модели. В случае нормального распределения остатков они образуют гауссовский белый шум.
Автокорреляция как функция целого аргумента s называется автокорреляционной функцией. График автокорреляционной функции называется коррелограммой. Поскольку при вычислении автокорреляций теряется часть информации (при сдвиге приходится убирать несколько первых наблюдений), то обычно принимается, что максимальный порядок автокорреляции может быть не более n/4, где n – длина временного ряда. Наряду с автокорреляционной функцией при исследовании временных рядов рассматривается также частная автокорреляционная функция, в которой используются частные коэффициенты автокорреляции, т.е. коэффициенты корреляции между членами временного ряда yt и yt+s при устранении влияния промежуточных (между yt и yt+s) членов.
По виду графиков автокорреляционной функции (ACF) и частной автокорреляционной функции (PACF) можно судить о структуре временного ряда.
Так, для стационарных стохастических временных рядов (если ряд действительно случаен) значения всех коэффициентов автокорреляции не должны выходить за пределы доверительной области нуля. Известно, что если ряд случаен (нет автокорреляции любого порядка), то доверительной областью нуля для него является (при достаточно больших n) интервал 0±2/ 
.
Вместо тестирования отличия от нуля коэффициентов автокорреляции каждого в отдельности, часто тестируют отличие от нуля сразу несколько таких коэффициентов подряд. Реализовать это можно при помощи Q-статистики Льюнга–Бокса (Ljung G., Box G.E.P.)
,
где n – объём выборки, а p – число одновременно тестируемых коэффициентов автокорреляции. Эта статистика проверяет нулевую гипотезу о том, что все p первых коэффициентов автокорреляции равны нулю, т.е. временной ряд является белым шумом. Если верна проверяемая гипотеза, Q-статистика имеет асимптотическое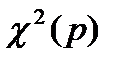 
-распределение (при достаточно большом числе уровней временного ряда). При относительно малых объёмах выборки этот тест может давать не совсем достоверные результаты.
Протестируем по этому тесту на стационарность следующий временной ряд (рисунок 1.1). (Если иного не будет указано, то в дальнейшем графики и все вычисления будут реализованы на основе эконометрического пакета прикладных программ EViews (Econometrics Views)).
Рисунок 1.1 – График тестируемого временного ряда
Построим для него коррелограмму. В результате получим (рисунок 1.2).
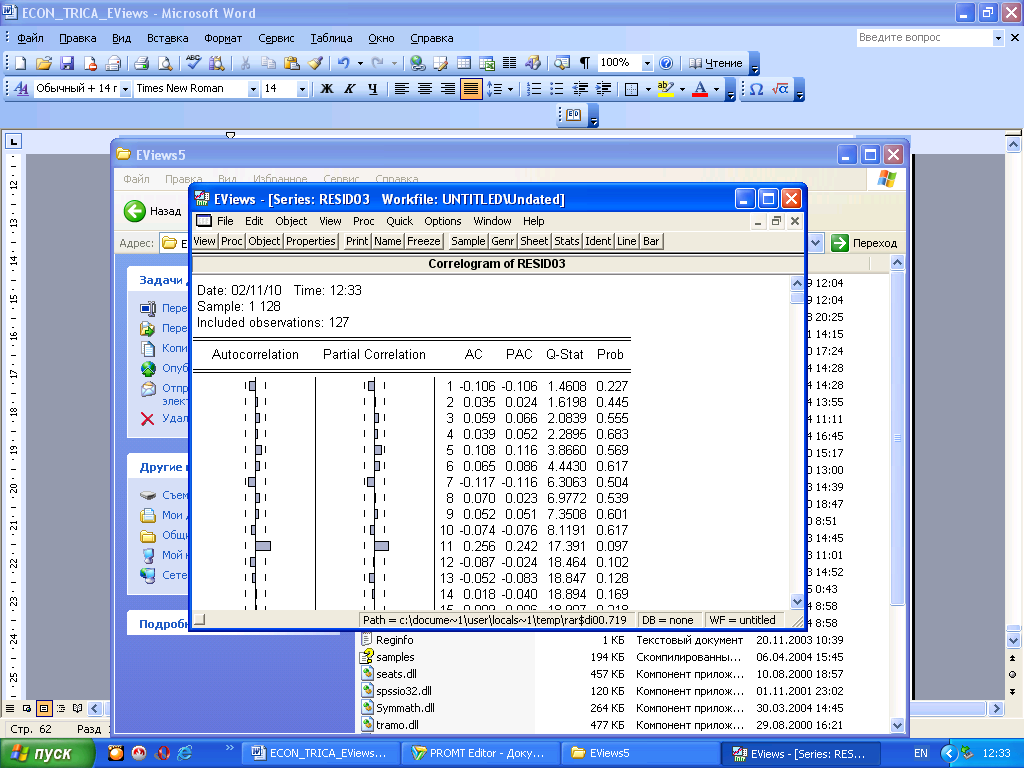
Рисунок 1.2 – Коррелограмма анализируемого ряда
На рисунке 1.2 последовательно изображено: в левой части рисунка помещены вертикальные графики автокорреляционной и частной автокорреляционной функций (вертикальные штриховые линии указывают доверительную область нуля), далее (первый столбик цифр) – порядок автокорреляции (s), затем значения соответствующих коэффициентов автокорреляции (AC) и частной автокорреляции (PAC). Последние два столбика цифр отражают значения Q-статистики и вероятностей, представляющих собой расчётные уровни значимости (Prob) для вычисленных значений Q-статистик. Из графиков и значений расчётных уровней значимости видно, что, по крайней мере, до 10-го порядка включительно, значения коэффициентов автокорреляции равны нулю (не выходят за пределы доверительной области нуля и все расчётные уровни значимости больше 0,05). На основании этого можем сделать вывод, что ряд, изображённый на рисунке 1.2, является стационарным (белым шумом).
1.2. Компоненты временного ряда
Как отмечалось, уровни временного ряда формируются под воздействием множества факторов, действующих в течение различных по протяжённости промежутков времени. Если основные статистические характеристики временного ряда зависят от времени, то такие ряды являются нестационарными.
Систематическую составляющую, действующую в течение длительного промежутка времени и формирующую основную тенденцию изменения уровней элементов временного ряда, называют трендовой составляющей или трендом. В дальнейшем будем обозначать её через Tt.
Регулярные колебания уровней элементов временного ряда, формирующиеся под воздействием систематически повторяющихся причин (обычно в течение года), называют сезонной составляющей. Будем обозначать её через St.
Различают также циклическую составляющую, формирующуюся под воздействием долговременно действующих (более года), но нерегулярных факторов, например, экономических циклов. Здесь мы их рассматривать не будем, отнеся к трендовой составляющей.
Удалив из уровней элементов временного рада трендовую и сезонную компоненты, получим случайную составляющую, формирующуюся под воздействием других, в том числе случайных, кратковременно действующих факторов. Будем обозначать её через It. Относительно случайной составляющей будем предполагать, что она следует процессу белого шума.
Если составляющие элементов временного ряда объединяются в виде произведения, то получаем мультипликативную модель временного ряда. Если составляющие элементов временного ряда объединяются в виде суммы, то получаем аддитивную модель временного ряда.
Одна из форм математической записи этих моделей следующая:
мультипликативная yt = Tt· St· It,
аддитивная yt = Tt+ St+ It.
Процесс разложения элементов временного ряда на составляющие называется декомпозицией временного ряда.
Если ряд имеет тренд, то он является нестационарным. В зависимости от принадлежности временного ряда к тому или иному классу различаются методы их анализа и прогнозирования. Прежде чем перейти к их рассмотрению, рассмотрим примеры различных типов временных рядов.
Стационарный временной ряд, имеющий только случайную компоненту, рассмотрен ранее (рисунок 1.1).
Рассмотрим пример нестационарного временного ряда, имеющего линейный тренд с наложенной на него случайной компонентой. Если временной ряд имеет чётко выраженный тренд в виде какой-либо функции от времени, то говорят, что имеем ряд с детерминированным трендом. Такой ряд представлен на рисунке 1.3.
Рисунок 1.3 – График временного ряда с детерминированным
линейным трендом
Построим кореллограмму этого ряда (рисунок 1.4).
Рисунок 1.4 – Коррелограмма анализируемого ряда
Как видим, коэффициенты автокорреляции выходят за пределы доверительной области нуля, постепенно убывая, что означает, что этот ряд нестационарный, о чём свидетельствуют и уровни значимости Q-статистики.
Рассмотрим график ряда со всеми тремя составляющими – трендовой, сезонной и случайной (рисунок 1.5). Здесь и график ряда, и коррелограмма, построены в другом статистическом пакете (Statgraphics Plus). В нашем случае длина сезонности равна четырём, что и отражено в коррелограмме (рисунок 1.6).
Рисунок 1.5 – Горизонтальный график временного ряда с сезонной составляющей и трендом
Как видим, наибольший коэффициент автокорреляции наблюдается при лаге, равном 4, это и указывает на сезонную составляющую, длина которой равна четырём. Наличие тренда отражено значимым коэффициентом автокорреляции первого порядка.
Рисунок 1.6 – Коррелограмма для временного ряда с сезонной составляющей и трендом
На рисунке 1.6 коррелограмма изображена в виде горизонтального графика, причём здесь показаны только коэффициенты автокорреляции без проверки гипотезы о стационарности ряда.
Из рассмотренного можно сделать вывод, что по виду коррелограммы можно судить о структуре временного ряда. Если ряд имеет детерминированный тренд, то несколько первых коэффициентов автокорреляции значимо отличны от нуля (выходят за пределы доверительной области нуля), а если при этом ещё имеется сезонная составляющая, то на лаге, равном длине сезонности, имеется «всплеск» коэффициента автокорреляции.
В зависимости от принадлежности временного ряда к тому или иному классу различаются методы их анализа и прогнозирования. Прежде чем перейти к их рассмотрению, введём показатели точности прогноза.
1.3. Показатели точности прогноза
Любой прогноз несёт на себе определённую степень ошибки, поэтому при проведении прогнозов на основе той или иной модели исследователь всегда имеет дело со случайными отклонениями прогнозных значений от их реальных текущих и будущих значений. Такие отклонения в случае правильной спецификации модели предполагаются распределёнными нормально, а мерой их рассеяния вокруг прогнозных значений служат различные показатели точности прогноза.
Рассмотрим некоторые из них. Пусть yt – реальные значения показателей временного ряда, а ft – прогнозные. Тогда ошибка прогноза в период времени t составит:
et = yt – ft.
Средняя ошибка прогноза (МЕ) определится из соотношения
и характеризует степень смещённости прогноза. В идеальном случае МЕ » 0. Если прогнозные значения в среднем завышены, то МЕ < 0, а если занижены, то МЕ > 0.
Средний квадрат ошибки прогноза (MSE) определяется из соотношения
.
Средняя абсолютная ошибка (МАЕ) вычисляется из соотношения:
.
MSE и МАЕ используются для сравнения процедур прогноза и подбора параметров сглаживания уровней элементов временного ряда.
Средняя абсолютная процентная ошибка (МРАЕ) вычисляется из соотношения:
и используется для оценки качества прогноза.
Если МРАЕ < 10%, то считается, что точность прогноза высокая, при 10% < МРАЕ < 20% – хорошая, если 20% < МРАЕ < 50%, то точность прогноза удовлетворительная и при МРАЕ > 50% – неудовлетворительная. МРАЕ вычисляется по ошибке прогноза на шаг вперёд.
Средняя процентная ошибка (МРЕ) вычисляется из соотношения:
и служит показателем смещённости прогноза (не должна превышать 5%).
Кроме того, в некоторых статистических пакетах прикладных программ корень квадратный из MSE называется стандартной ошибкой и обозначается RMSE.
Из разработанных и используемых в практике методов анализа временных рядов рассмотрим лишь несколько наиболее простых, часто используемых на практике и теоретически обоснованных.
1.4. Сглаживание уровней временных рядов
Этот метод анализа применяется в основном для выявления основной тенденции в развитии исследуемого явления и предназначен для устранения высокочастотных колебаний в уровнях временного ряда. Хотя с помощью этого метода можно устранить и сезонные колебания, выбрав в качестве интервала усреднения длину сезонности.
Среди множества различных вариантов этого метода наиболее простым является вычисление простой скользящей средней. При этом сначала выбирается длина интервала сглаживания и вычисленное значение средней арифметической на этом интервале в начале ряда присваивается его середине. Затем это действие сдвигается по уровням ряда на один элемент вправо и расчёты повторяются, т.е. вычисление средней арифметической как бы скользит по уровням ряда. Отсюда и название метода.
Данный метод наиболее эффективен при линейной динамике уровней ряда. В более общем случае используются методы взвешенной скользящей средней. Наиболее часто из них применяется метод экспоненциально взвешенной скользящей средней. В этом методе учитывается старение информации при удалении её от текущего момента времени.
Рассмотрим простую экспоненциально взвешенную среднюю. Пусть прогнозное значение для периода t рассчитывается по формуле
ft = 
yt + (1 - )yt-1 + (1 - )2 yt-2 +…+ (1 - )n yt- n + …,
где – показатель, характеризующий вес текущего наблюдения, называемый параметром сглаживания (0 < < 1).
Теоретически здесь предполагается бесконечный временной ряд с коэффициентами при лаговых значениях уровней временного ряда, убывающих по экспоненте. В силу того, что 0 < < 1, коэффициенты-веса при соответствующих элементах временного ряда быстро убывают, и достаточно несколько первых слагаемых этой суммы, чтобы получить результат с достаточной точностью.
Преобразуем это выражение. Вынесем за скобку (1 - ):
ft = yt + (1 - ) [ yt-1 + (1 - )yt-2 +…+ (1 - )n-1 yt-n + … ].
В квадратных скобках получили значение для ft- 1. Тогда можем записать:
ft = yt + (1 - )ft-1. (1.1)
Тем самым мы получили модель экспоненциально взвешенной скользящей средней. Из (1.1) следует, что для того, чтобы вычислить экспоненциально взвешенную скользящую среднюю нет необходимости вычислять сумму длинного числового ряда, необходимо знать только значение уровня временного ряда в текущем периоде и экспоненциально взвешенную скользящую среднюю за предыдущий период.
Отметим, что сумма весов в выражении экспоненциально взвешенной средней (как сумма бесконечно убывающей геометрической прогрессии) равна единице.
Параметр сглаживания обычно подбирается по минимальной ошибке прогноза. С этой целью перебираются возможные значения и для каждого из них рассчитываются экспоненциально взвешенные средние и для нихт – ошибка прогноза, например, MSE. Минимальная ошибка и определит константу сглаживания. При расчётах на ЭВМ особых проблем при подборе не возникает ввиду автоматизации таких расчётов. Возможен и ручной вариант подбора значения этой константы.
После простого преобразования модели (1.1) экспоненциально взвешенные скользящие средние могут быть представлены в виде
ft = ft-1+ (yt - ft-1).
Данная форма представления модели оправдывает её название как адаптивной модели прогнозирования. По этой модели прогноз на очередной период t+1 равен предыдущему прогнозу плюс доля ошибки предыдущего прогноза, т.е. в модели учитываются результаты предыдущих прогнозов, т.е. прогноз на очередной период как бы адаптируется к результатам предыдущих прогнозов.
Есть разные рекомендации по выбору возможных значений , основная из них заключается в том, что при анализе стационарных временных рядов параметр сглаживания не должен выходить за пределы интервала 0,05 – 0,3. Считается, что если ошибка прогноза уменьшается при выходе значения за пределы указанного интервала, то это означает, что речь идёт о не стационарном временном ряде.
Следует отметить, что, как следует из (1.1), прогнозные значения при увеличении более динамичны и в б о льшей мере отражают динамику исходных данных и, наоборот, чем меньше , тем прогнозные значения более сглажены. Поэтому, когда по ходу решения задачи требуется повысить чувствительность прогноза к динамике исходных данных, то высокие значения вполне оправданы.
Отметим, что при расчётах по модели (1.1) встаёт проблема определения прогнозного значения на начальный период (при t = 1, т.е. f0). Обычно за f0 берут либо y1, либо среднее значение нескольких первых членов ряда. Как правило, на конечный результат расчётов выбор начального значения f0 практически не сказывается.
Приведём пример использования экспоненциально взвешенных скользящих средних. Рассмотрим (рисунок 1.7). Верхняя левая часть этого рисунка – это график исходного ряда, верхняя правая – экспоненциально взвешенная скользящая средняя с = 0,6, нижняя левая – с = 0,3 и нижняя правая – с = 0,1. Как видим, чем больше , тем более гладкий ряд экспоненциально взвешенных скользящих средних.
Рисунок 1.7 – Экспоненциально взвешенные скользящие средние
1.5. Аналитическое выравнивание временных рядов
На практике часто приходится определять функциональную зависимость уровней временного ряда от времени. С этой целью сначала необходимо выполнить выравнивание уровней временного ряда, используя одну из возможных процедур, разработанных для этих целей. После этого вид динамики просматривается более чётко.
Процесс определения зависимости уровней временного ряда как функции от времени называется аналитическим выравниванием временных рядов. Обычно такую зависимость определяют, используя обычный метод наименьших квадратов, в котором в качестве независимой переменной выступает фактор времени. При таком подходе изменение исследуемого показателя связывают лишь с течением времени; считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени.
Прогнозирование исследуемого показателя на перспективу при этом осуществляется на основе экстраполяции, т.е. на продление в будущее тенденции, наблюдавшейся в прошлом, путём подстановки в аналитически выраженную зависимость от времени значений будущих тактов времени. При этом к такой форме зависимости предъявляются все те требования, которые разработаны для классического регрессионного анализа.
Для иллюстрации применения аналитического выравнивания временного ряда рассмотрим рисунок 1.8, в котором изображены графики реального временного ряда, выравненный временной ряд по линейному тренду и график остатков уравнения тренда. Необходимо помнить, что на подобных графиках помещены две вертикальные оси координат: правая – для исходной информации, левая – для остатков.
На рисунке 1.9 приведены уравнение линейного тренда, показатели его точности и адекватности. Ясно, что данное уравнение тренда неадекватно отражает динамику временного ряда(статистика Дарбина-Уотсона близка к нулю), но пока цель определения адекватного тренда и не ставилась (здесь иллюстрируется сама идея аналитического определения уравнения тренда).
Рисунок 1.8 – Графики уравнения линейного тренда
Рисунок 1.9 – Уравнение линейного тренда
Уравнение тренда в нашем случае имеет вид (с округлениями).
yt = 9,71 + 0,21t + et.
Здесь et – остатки, которые, как мы видим и по рисунку, и по статистике Дарбина – Уотсона, автокоррелированы (методы избавления от автокорреляции те же, что и в классическом регрессионном анализе).
Подставляя в это уравнение вместо t значения за пределами наблюдаемых значений (>50), будем получать прогнозные значения, вычисленные по тренду. При необходимости можно будет получить и интервальную оценку прогноза.
Здесь не приводится обсуждение разнообразия видов трендов, поскольку их разнообразие так велико, что только их перечень занял бы много места. При необходимости с этим можно ознакомиться в дополнительной литературе по эконометрике.
1.6. Проверка стабильности модели тренда (тест Чоу)
Идея этого теста связана с проверкой стабильности изучаемого процесса, в том числе для выявления стабильности тенденции временного ряда. Этот тест может быть реализован в двух вариантах. Один из них – Chow breakpoint test – основан на проверке гипотезы о сохранении значений всех коэффициентов модели при переходе от одного подпериода полного периода наблюдений к другому. Другой вариант теста Чоу (на качество прогноза – Chow forecast test) сравнивает качество прогноза, сделанного на основе оценивания модели на одной части периода, с качеством прогноза, сделанного на основе оценивания модели на всём периоде наблюдений.
Рассмотрим первый вариант. Допустим, что тенденция ряда имеет нестабильную тенденцию. Это значит, что, начиная с некоторого момента времени t = n1, происходит изменение характера динамики изучаемого показателя, что приводит к изменению параметров тренда, описывающего эту динамику. Это означает, что момент времени n1 сопровождается значительными изменениями ряда факторов, оказывающих воздействие на изучаемый показатель. При этом весь ряд динамики будем считать выборкой, которую можно разделить на две подвыборки: до момента n1 и после момента n1. При проведении теста предполагается, что на подвыборках может быть достигнута однородность информации.
Для проверки гипотезы о том, что исходная выборка однородна и разбиение её на две части не приведёт к значимому изменению оценок моделей, оценённых на подвыборках, находят параметры трёх уравнений тренда. Первое уравнение строится для всей совокупности наблюдений, второе и третье – для соответствующих выделенных подмножеств совокупности наблюдений. Для каждого из этих уравнений находят остаточную сумму квадратов SSE = Σei2. Для общего уравнения обозначим её через SSE0, а для уравнений по подмножествам – через SSE1 и SSE2 соответственно. Тогда равенство SSE0 = SSE1 + SSE2 выполняется, если оценки параметров всех трёх трендов совпадают (совокупность однородная).
В противном случае SSE0 > SSE1 + SSE2 и чем больше разница между разными частями этого неравенства, тем больше различие между двумя подмножествами с точки зрения значения оценок параметров уравнений трендов. Существенность различия проверяют с помощью F -критерия. Его фактическое значение находят по формуле
,
где m – число оцениваемых параметров уравнения тренда (без свободного члена), одинаковое для каждого уравнения. Если значение вычисленной статистики оказалось больше табличного (или, что всё равно, расчётный уровень значимости оказался меньше принятого), то гипотеза об однородности отклоняется и считается, что имеют место структурные сдвиги и целесообразно строить уравнение тренда для каждого подмножества в отдельности.
Рассмотренный критерий может быть применён для тестирования однородности выборки (проверки стабильности модели) при разбиении всей выборки на несколько подвыборок. В этом случае при проведении расчётов, например в EViews, надо указать точки деления выборки на подвыборки и тест проверит, есть ли существенное различие в указанных подвыборках.
Идея критерия Чоу на качества прогноза сходна с рассмотренным методом. Но есть и различия. Рассмотрим его подробнее.
Сначала оцениваются параметры модели тренда и значения уровней элементов временного ряда по всей совокупности наблюдений. Затем совокупность наблюдений разбивается на две части: по первой части оцениваются параметры модели тренда и по оценённой таким образом модели прогнозируются уровни элементов временного ряда для второй части выборки. После этого проверяется, значимо ли различаются оценённые значения уровней ряда для второй части выборки по двум моделям. Если модель стабильна, то это различие не должно быть значимым. Степень различия измеряет статистика
F =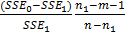 
,
где n1 – объём первой части выборки;
SSE0 – остаточная сумма квадратов модели, оценённой по всей выборке;
SSE1 – остаточная сумма квадратов модели, оценённой по первой части выборки объёма n1.
Если модель стабильна, то указанная статистика имеет распределение Фишера и гипотеза о стабильности отклоняется, если вычисленное значение этой статистики превышает табличное значение при заданном уровне значимости (или, что то же, если расчётный уровень значимости окажется меньше принятого).
Проиллюстрируем работу теста Чоу на примере проверки гипотезы об отсутствии структурных изменений в значении переменной lnGDP (поквартальные данные), уравнение линейного тренда дл