CPC
Тема: Анализ временных рядов
Проверила: Оспанова Г.К.
Выполнила: Мухаметжанова А. 346 ОМ
Астана 2014
Содержание
Введение
Классификация временных рядов
Методы анализа временных рядов
Заключение
Литература
Введение
Исследование динамики социально-экономических явлений, выявление и характеристика основных тенденций развития и моделей взаимосвязи дает основание для прогнозирования, то есть определения будущих размеров экономического явления.
Особенно актуальными становятся вопросы прогнозирования в условиях перехода на международные системы и методики учета и анализа социально-экономических явлений.
Важное место в системе учета занимают статистические методы. Применение и использование прогнозирования предполагает, что закономерность развития, действующая в прошлом, сохраняется и прогнозируемом будущем.
Таким образом, изучение методов анализа качества прогнозов является сегодня очень актуальным. Именно эта тема выбрана в качестве объекта исследования в данной работе.
Анализ временных рядов — совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогноза. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
Временной ряд — это упорядоченная по времени последовательность значений некоторой произвольной переменной величины. Каждое отдельное значение данной переменной называется отсчётом временного ряда. Тем самым, временной ряд существенным образом отличается от простой выборки данных.
Классификация временных рядов
Временные ряды классифицируются по следующим признакам.
1. По форме представления уровней:
Ø ряды абсолютных показателей;
Ø относительных показателей;
Ø средних величин.
2. По характеру временного параметра:
Ø моментные. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные периоды времени.
Ø интервальные временные ряды. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней.
3. По расстоянию между датами и интервалами времени:
Ø полные (равноотстоящие) – когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами.
Ø неполные (не равноотстоящие) – когда принцип равных интервалов не соблюдается.
4. В зависимости от наличия основной тенденции:
Ø стационарные ряды – в которых среднее значение и дисперсия постоянны.
Ø нестационарные – содержащие основную тенденцию развития.
Методы анализа временных рядов
Временные ряды исследуются с различными целями. В одном ряде случаях бывает достаточно получить описание характерных особенностей ряда, а в другом ряде случаев требуется не только предсказывать будущие значения временного ряда, но и управлять его поведением. Метод анализа временного ряда определяется, с одной стороны, целями анализа, а с другой стороны, вероятностной природой формирования его значений.
Методы анализа временных рядов.
1. Спектральный анализ. Позволяет находить периодические составляющие временного ряда.
2. Корреляционный анализ. Позволяет находить существенные периодические зависимости и соответствующие им задержки (лаги) как внутри одного ряда (автокорреляция), так и между несколькими рядами. (кросскорреляция)
3. Сезонная модель Бокса-Дженкинса. Применяется когда временной ряд содержит явно выраженный линейный тренд и сезонные составляющие. Позволяет предсказывать будущие значения ряда. Модель была предложена в связи с анализом авиаперевозок.
4. Прогноз экспоненциально взвешенным скользящим средним. Простейшая модель прогнозирования временного ряда. Применима во многих случаях. В том числе, охватывает модель ценообразования на основе случайных блужданий.
Цель спектрального анализа - разложить ряд на функции синусов и косинусов различных частот, для определения тех, появление которых особенно существенно и значимо. Один из возможных способов сделать это - решить задачу линейной множественной регрессии, где зависимая переменная - наблюдаемый временной ряд, а независимые переменные или регрессоры: функции синусов всех возможных (дискретных) частот. Такая модель линейной множественной регрессии может быть записана как:
xt = a0 + 
[ak*cos(
k*t) + bk*sin( k*t)] (для k = 1 до q)
Следующее общее понятие классического гармонического анализа в этом уравнении - (лямбда) -это круговая частота, выраженная в радианах в единицу времени, т.е. = 2*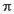 
* 
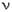k, где 
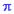- константа пи = 3.1416 и 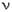k = k/q. Здесь важно осознать, что вычислительная задача подгонки функций синусов и косинусов разных длин к данным может быть решена с помощью множественной линейной регрессии. Заметим, что коэффициенты ak при косинусах и коэффициенты bk при синусах - это коэффициенты регрессии, показывающие степень, с которой соответствующие функции коррелируют с данными. Всего существует q различных синусов и косинусов; интуитивно ясно, что число функций синусов и косинусов не может быть больше числа данных в ряде. Не вдаваясь в подробности, отметим, если n - количество данных, то будет n/2+1 функций косинусов и n/2-1 функций синусов. Другими словами, различных синусоидальных волн будет столько же, сколько данных, и вы сможете полностью воспроизвести ряд по основным функциям.
В итоге, спектральный анализ определяет корреляцию функций синусов и косинусов различной частоты с наблюдаемыми данными. Если найденная корреляция (коэффициент при определенном синусе или косинусе) велика, то можно заключить, что существует строгая периодичность на соответствующей частоте в данных.
Анализ распределенных лагов - это специальный метод оценки запаздывающей зависимости между рядами. Например, предположим, вы производите компьютерные программы и хотите установить зависимость между числом запросов, поступивших от покупателей, и числом реальных заказов. Вы могли бы записывать эти данные ежемесячно в течение года и затем рассмотреть зависимость между двумя переменными: число запросов и число заказов зависит от запросов, но зависит с запаздыванием. Однако очевидно, что запросы предшествуют заказам, поэтому можно ожидать, что число заказов. Иными словами, в зависимости между числом запросов и числом продаж имеется временной сдвиг (лаг) (см. также автокорреляции и кросскорреляции).
Такого рода зависимости с запаздыванием особенно часто возникают в эконометрике. Например, доход от инвестиций в новое оборудование отчетливо проявится не сразу, а только через определенное время. Более высокий доход изменяет выбор жилья людьми; однако эта зависимость, очевидно, тоже проявляется с запаздыванием.
Во всех этих случаях, имеется независимая или объясняющая переменная, которая воздействует на зависимые переменные с некоторым запаздыванием (лагом). Метод распределенных лагов позволяет исследовать такого рода зависимость.
Общая модель
Пусть y - зависимая переменная, a независимая или объясняющая x. Эти переменные измеряются несколько раз в течение определенного отрезка времени. В некоторых учебниках по эконометрике зависимая переменная называется также эндогенной переменной, a зависимая или объясняемая переменная экзогенной переменной. Простейший способ описать зависимость между этими двумя переменными дает следующее линейное уравнение:
Yt =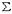 
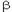i*xt-i
В этом уравнении значение зависимой переменной в момент времени t является линейной функцией переменной x, измеренной в моменты t, t-1, t-2 и т.д. Таким образом, зависимая переменная представляет собой линейные функции x и x, сдвинутых на 1, 2, и т.д. временные периоды. Бета коэффициенты (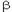 i) могут рассматриваться как параметры наклона в этом уравнении. Будем рассматривать это уравнение как специальный случай уравнения линейной регрессии. Если коэффициент переменной с определенным запаздыванием (лагом) значим, то можно заключить, что переменная y предсказывается (или объясняется) с запаздыванием.
Процедуры оценки параметров и прогнозирования, описанные в разделе, предполагают, что математическая модель процесса известна. В реальных данных часто нет отчетливо выраженных регулярных составляющих. Отдельные наблюдения содержат значительную ошибку, тогда как вы хотите не только выделить регулярные компоненты, но также построить прогноз. Методология АРПСС, разработанная Боксом и Дженкинсом (1976), позволяет это сделать. Данный метод чрезвычайно популярен во многих приложениях, и практика подтвердила его мощность и гибкость (Hoff, 1983; Pankratz, 1983; Vandaele, 1983). Однако из-за мощности и гибкости, АРПСС - сложный метод. Его не так просто использовать, и требуется большая практика, чтобы овладеть им. Хотя часто он дает удовлетворительные результаты, они зависят от квалификации пользователя (Bails and Peppers, 1982). Следующие разделы познакомят вас с его основными идеями. Для интересующихся кратким, рассчитанным на применение, (нематематическим) введением в АРПСС, рекомендуем книгу McCleary, Meidinger, and Hay (1980).
Модель АРПСС
Общая модель, предложенная Боксом и Дженкинсом (1976) включает как параметры авторегрессии, так и параметры скользящего среднего. Именно, имеется три типа параметров модели: параметры авто регрессии (p), порядок разности (d), параметры скользящего среднего (q). В обозначениях Бокса и Дженкинса модель записывается как АРПСС (p, d, q). Например, модель (0, 1, 2) содержит 0 (нуль) параметров авто регрессии (p) и 2 параметра скользящего среднего (q), которые вычисляются для ряда после взятия разности с лагом 1.
Как отмечено ранее, для модели АРПСС необходимо, чтобы ряд был стационарным, это означает, что его среднее постоянно, а выборочные дисперсия и автокорреляция не меняются во времени. Поэтому обычно необходимо брать разности ряда до тех пор, пока он не станет стационарным (часто также применяют логарифмическое преобразование для стабилизации дисперсии). Число разностей, которые были взяты, чтобы достичь стационарности, определяются параметром d (см. предыдущий раздел). Для того чтобы определить необходимый порядок разности, нужно исследовать график ряда и автокоррелограмму. Сильные изменения уровня (сильные скачки вверх или вниз) обычно требуют взятия несезонной разности первого порядка (лаг=1). Сильные изменения наклона требуют взятия разности второго порядка. Сезонная составляющая требует взятия соответствующей сезонной разности (см. ниже). Если имеется медленное убывание выборочных коэффициентов автокорреляции в зависимости от лага, обычно берут разность первого порядка. Однако следует помнить, что для некоторых временных рядов нужно брать разности небольшого порядка или вовсе не брать их. Заметим, что чрезмерное количество взятых разностей приводит к менее стабильным оценкам коэффициентов.
На этом этапе (который обычно называют идентификацией порядка модели, см. ниже) вы также должны решить, как много параметров авто регрессии (p) и скользящего среднего (q) должно присутствовать в эффективной и экономной модели процесса. (Экономность модели означает, что в ней имеется наименьшее число параметров и наибольшее число степеней свободы среди всех моделей, которые подгоняются к данным). На практике очень редко бывает, что число параметров p или q больше 2 (см. ниже более полное обсуждение).
Следующий, после идентификации, шаг (Оценивание) состоит в оценивании параметров модели (для чего используются процедуры минимизации функции потерь, см. ниже; более подробная информация о процедурах минимизации дана в разделе Нелинейное оценивание). Полученные оценки параметров используются на последнем этапе (Прогноз) для того, чтобы вычислить новые значения ряда и построить доверительный интервал для прогноза. Процесс оценивания проводится по преобразованным данным (подвергнутым применению разностного оператора). До построения прогноза нужно выполнить обратную операцию (интегрировать данные). Таким образом, прогноз методологии будет сравниваться с соответствующими исходными данными. На интегрирование данных указывает буква П в общем названии модели (АРПСС = Авто регрессионное Проинтегрированное Скользящее Среднее).
Дополнительно модели АРПСС могут содержать константу, интерпретация которой зависит от подгоняемой модели. Именно, если (1) в модели нет параметров авто регрессии, то константа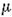 
есть среднее значение ряда, если (2) параметры авто регрессии имеются, то константа представляет собой свободный член. Если бралась разность ряда, то константа представляет собой среднее или свободный член преобразованного ряда. Например, если бралась первая разность (разность первого порядка), а параметров авто регрессии в модели нет, то константа представляет собой среднее значение преобразованного ряда и, следовательно, коэффициент наклона линейного тренда исходного.
Экспоненциальное сглаживание - это очень популярный метод прогнозирования многих временных рядов. Исторически метод был независимо открыт Броуном и Холтом.
Простое экспоненциальное сглаживание
Простая и прагматически ясная модель временного ряда имеет следующий вид:
Xt = b +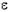 
t,
где b - константа и 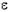(эпсилон) - случайная ошибка. Константа b относительно стабильна на каждом временном интервале, но может также медленно изменяться со временем. Один из интуитивно ясных способов выделения b состоит в том, чтобы использовать сглаживание скользящим средним, в котором последним наблюдениям приписываются большие веса, чем предпоследним, предпоследним большие веса, чем пред предпоследним и т.д. Простое экспоненциальное именно так и устроено. Здесь более старым наблюдениям приписываются экспоненциально убывающие веса, при этом, в отличие от скользящего среднего, учитываются все предшествующие наблюдения ряда, а не те, что попали в определенное окно. Точная формула простого экспоненциального сглаживания имеет следующий вид:
St =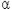 
*Xt + (1- 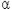)*St-1
Когда эта формула применяется рекурсивно, то каждое новое сглаженное значение (которое является также прогнозом) вычисляется как взвешенное среднее текущего наблюдения и сглаженного ряда. Очевидно, результат сглаживания зависит от параметра 
(альфа). Если равно 1, то предыдущие наблюдения полностью игнорируются. Если равно 0, то игнорируются текущие наблюдения. Значения между 0, 1 дают промежуточные результаты.
Эмпирические исследования Makridakis и др. (1982; Makridakis, 1983) показали, что весьма часто простое экспоненциальное сглаживание дает достаточно точный прогноз.
Выбор лучшего значения параметра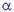 
(альфа)
Gardner (1985) обсуждает различные теоретические и эмпирические аргументы в пользу выбора определенного параметра сглаживания. Очевидно, из формулы, приведенной выше, следует, что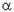 
должно попадать в интервал между 0 (нулем) и 1 (хотя Brenner et al., 1968, для дальнейшего применения анализа АРПСС считают, что 0< 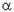<2). Gardner (1985) сообщает, что на практике обычно рекомендуется брать 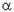меньше.30. Однако в исследовании Makridakis et al., (1982), 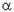большее.30, часто дает лучший прогноз. После обзора литературы, Gardner (1985) приходит к выводу, что лучше оценивать оптимально 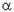по данным (см. ниже), чем просто "гадать" или использовать искусственные рекомендации.
Оценивание лучшего значения 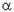с помощью данных. На практике параметр сглаживания часто ищется с поиском на сетке. Возможные значения параметра разбиваются сеткой с определенным шагом. Например, рассматривается сетка значений от 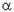= 0.1 до 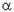= 0.9, с шагом 0.1. Затем выбирается 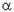, для которого сумма квадратов (или средних квадратов) остатков (наблюдаемые значения минус прогнозы на шаг вперед) является минимальной.
Индексы качества подгонки
Самый прямой способ оценки прогноза, полученного на основе определенного значения 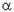- построить график наблюдаемых значений и прогнозов на один шаг вперед. Этот график включает в себя также остатки (отложенные на правой оси Y). Из графика ясно видно, на каких участках прогноз лучше или хуже.
Такая визуальная проверка точности прогноза часто дает наилучшие результаты. Имеются также другие меры ошибки, которые можно использовать для определения оптимального параметра 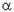(см. Makridakis, Wheelwright, and McGee, 1983):
Средняя ошибка. Средняя ошибка (СО) вычисляется простым усреднением ошибок на каждом шаге. Очевидным недостатком этой меры является то, что положительные и отрицательные ошибки аннулируют друг друга, поэтому она не является хорошим индикатором качества прогноза.
Средняя абсолютная ошибка. Средняя абсолютная ошибка (САО) вычисляется как среднее абсолютных ошибок. Если она равна 0 (нулю), то имеем совершенную подгонку (прогноз). В сравнении со средней квадратической ошибкой, эта мера "не придает слишком большого значения" выбросам.
Сумма квадратов ошибок (SSE), среднеквадратическая ошибка. Эти величины вычисляются как сумма (или среднее) квадратов ошибок. Это наиболее часто используемые индексы качества подгонки.
Относительная ошибка (ОО). Во всех предыдущих мерах использовались действительные значения ошибок. Представляется естественным выразить индексы качества подгонки в терминах относительных ошибок. Например, при прогнозе месячных продаж, которые могут сильно флуктуировать (например, по сезонам) из месяца в месяц, вы можете быть вполне удовлетворены прогнозом, если он имеет точность?10%. Иными словами, при прогнозировании абсолютная ошибка может быть не так интересна как относительная. Чтобы учесть относительную ошибку, было предложено несколько различных индексов (см. Makridakis, Wheelwright, and McGee, 1983). В первом относительная ошибка вычисляется как:
ООt = 100*(Xt - Ft)/Xt
где Xt - наблюдаемое значение в момент времени t, и Ft - прогноз (сглаженное значение).
Средняя относительная ошибка (СОО). Это значение вычисляется как среднее относительных ошибок.
Средняя абсолютная относительная ошибка (САОО). Как и в случае с обычной средней ошибкой отрицательные и положительные относительные ошибки будут подавлять друг друга. Поэтому для оценки качества подгонки в целом (для всего ряда) лучше использовать среднюю абсолютную относительную ошибку. Часто эта мера более выразительная, чем среднеквадратическая ошибка. Например, знание того, что точность прогноза ±5%, полезно само по себе, в то время как значение 30.8 для средней квадратической ошибки не может быть так просто проинтерпретировано.
Автоматический поиск лучшего параметра. Для минимизации средней квадратической ошибки, средней абсолютной ошибки или средней абсолютной относительной ошибки используется квази-ньютоновская процедура (та же, что и в АРПСС). В большинстве случаев эта процедура более эффективна, чем обычный перебор на сетке (особенно, если параметров сглаживания несколько), и оптимальное значение 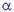можно быстро найти.
Первое сглаженное значение S0. Если вы взгляните снова на формулу простого экспоненциального сглаживания, то увидите, что следует иметь значение S0 для вычисления первого сглаженного значения (прогноза). В зависимости от выбора параметра 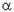(в частности, если 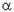близко к 0), начальное значение сглаженного процесса может оказать существенное воздействие на прогноз для многих последующих наблюдений. Как и в других рекомендациях по применению экспоненциального сглаживания, рекомендуется брать начальное значение, дающее наилучший прогноз. С другой стороны, влияние выбора уменьшается с длиной ряда и становится некритичным при большом числе наблюдений.
экономический временный ряд статистический
Заключение
Анализ временных рядов — совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогноза. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
Временные ряды исследуются с различными целями. Метод анализа временного ряда определяется, с одной стороны, целями анализа, а с другой стороны, вероятностной природой формирования его значений.
Основными методами исследования временных рядов являются:
Ø Спектральный анализ.
Ø Корреляционный анализ
Ø Сезонная модель Бокса-Дженкинса.
Ø Прогноз экспоненциально взвешенным скользящим средним.
Литература
1. Безручко Б. П., Смирнов Д. А. Математическое моделирование и хаотические временные ряды. — Саратов: ГосУНЦ "Колледж", 2005. — ISBN 5-94409-045-6
2. Блехман И. И., Мышкис А. Д., Пановко Н. Г., Прикладная математика: Предмет, логика, особенности подходов. С примерами из механики: Учебное пособие. — 3-е изд., испр. и доп. — М.: УРСС, 2006. — 376 с. ISBN 5-484-00163-3
3. Введение в математическое моделирование. Учебное пособие. Под ред. П. В. Трусова. — М.: Логос, 2004. — ISBN 5-94010-272-7
4. Горбань А. Н., Хлебопрос Р. Г., Демон Дарвина: Идея оптимальности и естественный отбор. — М: Наука. Гл ред. физ.-мат. лит., 1988. — 208 с. (Проблемы науки и технического прогресса) ISBN 5-02-013901-7 (Глава «Изготовление моделей»).
5. Журнал Математическое моделирование (основан в 1989 году)
6. Малков С. Ю., 2004. Математическое моделирование исторической динамики: подходы и модели // Моделирование социально-политической и экономической динамики / Ред. М. Г. Дмитриев. — М.: РГСУ. — с. 76-188.
7. Мышкис А. Д., Элементы теории математических моделей. — 3-е изд., испр. — М.: КомКнига, 2007. — 192 с ISBN 978-5-484-00953-4
8. Самарский А. А., Михайлов А. П. Математическое моделирование. Идеи. Методы. Примеры.. — 2-е изд., испр.. — М.: Физматлит, 2001. — ISBN 5-9221-0120-X
9. Советов Б. Я., Яковлев С. А., Моделирование систем: Учеб. для вузов — 3-е изд., перераб. и доп. — М.: Высш. шк., 2001. — 343 с. ISBN 5-06-003860-2
Размещено на Allbest.ru