Урок №118
Комбинированное занятие № 51
Тема: Уравнение касательной. Возрастание и убывание функции. Признаки возрастания и убывания функции.
Цель:
Учебная:
- познакомить обучающихся с применением производной;
Развивающая:
- формирование умений применять приемы сравнения, обобщения, выделения главного, логически излагать мысли, делать выводы, развивать речь, внимание и память.
Воспитательная:
- способствовать формированию умений применять приемы: сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.
Методы обучения: практическая работа, контрольная работа.
Оборудование: компьютер, проектор.
Тип урока: урок обобщения и систематизации знаний.
Формируемые на уроке ПК и ОК
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
План занятия.
1. Организационный момент.
2. Актуализация темы.
3. Уравнение касательной.
4. Возрастание и убывание функции.
5. Признаки возрастания и убывания функции.
6. Решение упражнений.
7. Домашнее задание.
8. Итоги занятия.
Ход занятия.
1. Организационный момент – приветствие, проверка посещаемости.
Актуализация темы.
Обучающиеся вспоминают, что такое предел функции.
Уравнение касательной.
ТЕОРЕМА. Пусть функция у = f (х) непрерывна на интервале (а; b) и имеет в точке х 0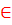 
(а; b) производную. Тогда график этой функции имеет в точке (х 0; f (х 0)) касательную, уравнение которой у – у 0 = k (х – х 0), где у 0 = f (х 0),
k = f ʹ(х 0).
Пример 1. Напишем уравнение касательной к графику функции f(x) = х 2, проходящей через точку графика с абсциссой х 0 = –2.
Функция f(x) = х 2 имеет производную f ʹ(x) = 2 х. Отсюда
у 0 = f (х 0) = (х 0)2 = (–2)2 = 4,
k = f ʹ(х 0) = 2 х 0 = 2 ∙ (–2) = – 4.
Согласно теореме, уравнение касательной имеет вид у – 4 = – 4 (х + 2),
т. е. у = – 4 х – 4.
Касательная к графику функции f (x) = х 2 в точке графика с абсциссой –2 изображена на рисунке ниже.
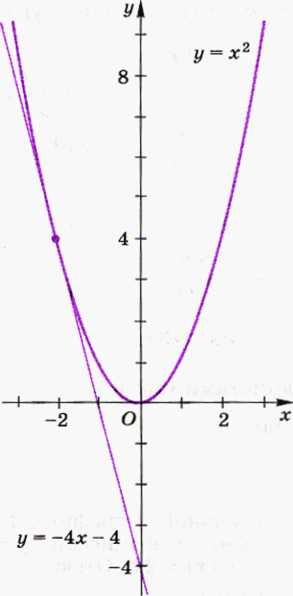
ПРИМЕР 2. Напишем уравнение касательной к графику функции
f (x) = – х 2 + 6 х – 7, параллельной прямой у = 4х + 5.
Вычислим угловой коэффициент k = f '(x 0) касательной к графику этой функции в точке с абсциссой х 0.
Так как f ʹ(х) = (– х 2 + 6х – 7)' = –2 х + 6, то k = f '(x 0) = –2 x 0+ 6.
По условию касательная должна быть параллельна прямой у = 4х + 5, следовательно, ее угловой коэффициент должен быть равен 4, т. е.
–2 x 0 + 6 = 4, откуда x 0 = 1.
Вычислим значение функции у = f (x) в точке x 0 = 1:
у 0 = f (х 0) = f (1) = –12 + 6 ∙ 1 – 7 = –2, тогда, согласно теореме, уравнение касательной имеет вид у + 2 = 4(х – 1), т. е. у = 4 х – 6.
Возрастание и убывание функции
Пусть функция f (x) непрерывна на промежутке I и имеет внутри промежутка производную f ʹ(х). Тогда:
1) если f ʹ(х) > 0 внутри промежутка I, то функция f возрастает на промежутке I;
2) если f ʹ(х) < 0 внутри промежутка I, то функция f убывает на промежутке I.
Утверждения 1 и 2 являются следствиями следующей теоремы:
ТЕОРЕМА. Пусть функция f (x) непрерывна на промежутке I и имеет производную f ʹ(х) в каждой точке внутри промежутка I. Тогда:
а) если f ʹ(х) > 0 для каждого х внутри промежутка I, то функция f (x) возрастает на промежутке I;
б) если f ʹ(х) < 0 для каждого х внутри промежутка I, то функция f (x) убывает на промежутке I;
в) если f ʹ(х) = 0 для каждого х внутри промежутка I, то функция f (x) постоянная (константа) на промежутке I.
Пример 1. Найдем промежутки возрастания функции
f (x) = x 3. (1)
Функция (1) непрерывна и имеет производную для всех х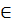 
R. Так как
f '(х) = (х 3)' = 3 х 2, то f (x) = 0 при х = 0 и f '(х) > 0 при х ≠ 0.
По утверждению 1 функция (1) возрастает на каждом из промежутков
(– 
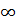; 0] и [0; + 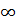). Но тогда функция (1) возрастает и на всем интервале
(– ; + ).
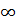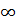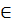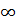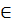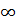В самом деле, пусть х 1 < х 2, тогда если х 2 (– ; 0] или х 1 [0; + ), то уже доказано, что f (x 1) < f (x 2). Остается случай f (x 1) < 0 < f (x 2). В этом случае из возрастания функции на промежутках (– 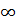; 0] и [0; + 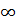) следует, что
f (x 1) < f (0) и f (0) < f (x 2), но тогда f (x 1) < f (x 2). Таким образом, функция (1) является возрастающей на всем интервале (– ; + ).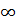
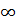ПРИМЕР 2. Найдем промежутки возрастания (убывания) функции
f (x) = ln(х 2 – 3). (2)
Функция (2) определена при х 2 – 3 > 0, т. е. на объединении интервалов
(– ; – 
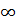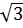) и (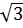; + 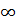). На каждом из этих интервалов функция (2) имеет производную. Так как
f '(х) =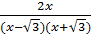 
,
то ни в одной из точек этих интервалов производная функции (2) не обращается в нуль.
Так как f '(х) > 0 для любых х > 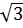и f '(х) < 0 для любых х < – 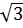, то по утверждениям 1 и 2 функция (2) возрастает на промежутке (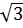; + 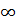) и убывает на промежутке (– 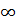; – 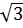). Она не определена на отрезке [– ; ].
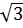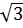Утверждения 1 и 2 позволяют определять, является ли критическая точка, в которой производная равна нулю, точкой локального максимума или точкой локального минимума.
Пусть функция f (x) имеет производную внутри промежутка I и критическая точка х 0 лежит внутри I, тогда:
а) если в точке х 0 производная меняет знак с «+» на «–», то х 0 – точка локального максимума;
б) если в точке х 0 производная меняет знак с «–» на «+», то х 0 – точка локального минимума.
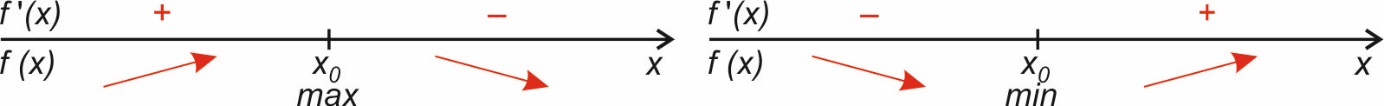
Пример 3. Найдем промежутки возрастания (убывания) и точки локального экстремума функции
f (x) = х 3 – 6 х 2 + 9 х – 1.
Функция f (x) имеет производную для всех х 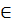R.
Так как f '(х) = (х 3 – 6 х 2 + 9 х – 1)' = 3 х 2 –12 х + 9 = 3(х – 1)(х – 3), то:
f '(х) = 0 при х = 1 и при х = 3;
f '(х) > 0 при х 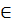(– 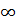; 1) и при х 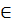(3; + );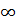
f '(х) < 0 при х 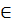(1; 3).
По утверждениям 1 и 2 функция f (x) возрастает на каждом из промежутков (– 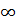; 1] и [3; + 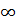), убывает на промежутке [1; 3] (рис.).
Следовательно, в точке х = 1 функция f (x) имеет локальный максимум, а в точке х = 3 – локальный минимум.
Домашнее задание
Учебник Башмакова, стр. 183-187
Учебник Никольского, 11 класс, §5.2, 5.5, №5.22(г), №5.50(в).
Итог урока
Обучающиеся отвечают на вопросы, что они сегодня изучили, что было понятно, а что нет.