| № | Вопросы и задания | Баллы |
| 1. | Какая сумма является десятичной записью числа? | |
| 2. | Обоснуйте содержание задания, используя понятие десятичной системы счисления и законы действий над числами. | |
| 3. | Выполните действия. | |
| Итого: |
| Вариант | Задание 1 | Задание 2 | Задание 3 |
| 1. | 724  5 5
| (29148:347+4095–312)  709 709
| |
| 2. | 342  6 6
| 1770048:504+2451  21–49978 21–49978
| |
| 3. | 784  3 3
| 14896:19  527–89795+5127 527–89795+5127
| |
| 4. | 921  2 2
| 54318–9705+8702:19  708 708
| |
| 5. | 548  7 7
| 527  216:4–19749+7997 216:4–19749+7997
| |
| 6. | 932  8 8
| (89777+78439):24–178  39 39
| |
| 7. | 324  4 4
| (325484-21524):408+395  709 709
| |
| 8. | 248  9 9
| 724  126:72+47954–48987 126:72+47954–48987
|
Проверочная работа №2
Запись чисел в системах счисления, отличных от десятичной
| № | Вопросы и задания | Баллы |
| 1. | Запишите числа 9, 38, 892, 1043 в р-ичной системе счисления. | |
| 2. | Запишите числа в порядке возрастания. | |
| 3. | При каком значении х верны равенства? | |
| Итого: |
| Вариант | Задание 1 | Задание 2 | Задание 3 |
| 1. | Р=2 | 24325, 34156, 11467 | 421х=111, 21х=7, х5=23 |
| 2. | Р=3 | 40859, 31368, 52436 | 111х=7, 256х=139, 244х=130 |
| 3. | Р=4 | 1221, 10435, 12134 | 23х=15, х3=121, 67х=55 |
| 4. | Р=5 | 21537, 1100112, 31425 | 222х=42, 564х=391, 276х=181 |
| 5. | Р=6 | 14728, 23657, 41235 | 5321х=1201, 1001х=9, 4123х=538 |
| 6. | Р=7 | 12468, 43256, 24315 | 2101х=64, 3344х=474, 10320х=312 |
| 7. | Р=8 | 32134, 12415, 22416 | 1425х=377, 872х=713, 34х=22 |
| 8. | Р=9 | 12507, 13809, 20256 | 351х=183, 643х=419, 251х=134 |
| 9. | Р=11 | 14178, 123255, 22123 | 324х=165, 312х=116, 521х=337 |
| 10. | Р=12 | 43678, 25437, 53236 | 126х=105, 343х=98, 123х=51 |
Проверочная работа №3
Арифметические действия над числами в различных системах счисления
| № п/п | Задания | Баллы |
| Найдите значение выражения и выполните проверку. | ||
| Выполните действия. | ||
| Выполните действия и запишите ответ в заданной системе счисления. | ||
| Итого: |
| Вариант | Задание 1 | Задание 2 | Задание 3 |
| 352678 + 53748 = | 6535167 + 5462367 – 20610217: 4237 · 3427 = | 1734528 + 3162278 = Х4 | |
| 210435 * 20455 = | (3489 · 269 + 343459: 549) – 18689 = | 353206: 526 = Х7 | |
| 103256 – 4536 = | (21023 · 213) + (10113: 123) + (20013 + 212203) – (12013 – 1223) = | 400456 – 55556 = Х7 | |
| 3204215: 425 = | 614557: 637 · 537 – 235467 + 5437 = | 3248 · 258 = Х5 | |
| 3365627 + 5643357 = | 455406: 536 · 4536 – (4536 + 5546) = | 303135: 425 = Х3 | |
| 345116 · 2456 = | 224445: 4315 · 3435 + 3445 – 4445 = | 325416 · 3426 = Х3 | |
| 104116 – 25456 = | 223125: 245 + 3415 · 235 – 43215 = | 310246 – 34216 = Х8 | |
| 3244125: 1245 = | 1111113: 12213 + 11213 · 1023 – 11113= | 7368 · 218 = Х7 | |
| 456378 + 434568 = | 6535167 + 5462367 – 20610217: 4237 · 3427 = | 176768 · 1348 = Х6 | |
| 231546 · 2136 = | 614557: 637 · 537 – 235467 + 5437 = | 345116 · 2456 = Х5 |
ТЕМА 2. ОСНОВЫТЕОРИИ ДЕЛИМОСТИ
Лекция 1. Делимость целых неотрицательных чисел
План
1. Отношение делимости и его свойства.
2. Делимость суммы, разности и произведения целых неотрицательных чисел.
3. Признаки делимости.
Содержание
1. На множестве целых неотрицательных чисел N0 рассмотрим отношение делимости.
Определение 1. Говорят, что целое неотрицательное число а делится на натуральное число b, если существует такое целое неотрицательное число q, что а = b · q.
Если а делится на b, то пишут: 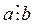 . Иногда говорят, что «а кратно b ». Обратным к отношению
. Иногда говорят, что «а кратно b ». Обратным к отношению 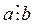 является отношение «b делит а ».
является отношение «b делит а ».
Отношение делимости 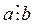 является бинарным отношением на множестве N0. Рассмотрим свойства, которыми оно обладает.
является бинарным отношением на множестве N0. Рассмотрим свойства, которыми оно обладает.
1. Отношение делимости рефлексивно, то есть
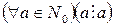 .
.
Справедливость этого свойства следует из того, что а = а · 1 и 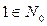 . Так что можно считать q = 1.
. Так что можно считать q = 1.
2. Отношение делимости антисимметрично, то есть
 .
.
Доказательство этого свойства проведем методом от противного. Предположим, что 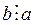 . Тогда, по теореме 22 о существовании и единственности частного, b ≥ а. Но по условию –
. Тогда, по теореме 22 о существовании и единственности частного, b ≥ а. Но по условию – 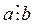 , и значит, а ≥ b. Выполнение обоих неравенств возможно только при а = b, что противоречит условию. Следовательно, справедливость свойства установлена.
, и значит, а ≥ b. Выполнение обоих неравенств возможно только при а = b, что противоречит условию. Следовательно, справедливость свойства установлена.
3. Отношение делимости транзитивно, то есть
 .
.
Действительно, поскольку 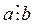 , то, по определению 1, существует такое
, то, по определению 1, существует такое  , что а = bq 1. Аналогично, существует
, что а = bq 1. Аналогично, существует 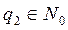 такое, что b = cq 2. Тогда
такое, что b = cq 2. Тогда 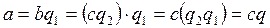 , где
, где  . Это и означает, что
. Это и означает, что  .
.
Таким образом, отношение делимости на множестве N0, обладая свойствами рефлексивности, антисимметричности и транзитивности, является отношением нестрогого порядка.
2. Рассмотрим ряд основных теорем, связанных с делимостью суммы, разности и произведения.
Теорема 1. Если каждое слагаемое суммы делится на натуральное число b, то и вся сумма делится на это число, то есть
 .
.
Доказательство. Пусть  . Тогда существуют
. Тогда существуют  такие, что выполняются равенства:
такие, что выполняются равенства:  . Из этих равенств следует, что
. Из этих равенств следует, что 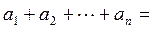
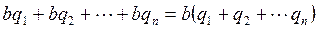 , где
, где  . По определению 1 отношения делимости это означает, что
. По определению 1 отношения делимости это означает, что 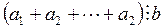 .
.
Теорема 2. Если каждое из чисел а и b делится на с и а ≥ b, то разность а – b делится на с, то есть
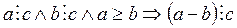 .
.
Доказательство. Пусть  и
и  . Тогда существуют
. Тогда существуют  такие, что
такие, что  и
и 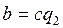 . Поскольку а ≥ b, то q 1 ≥ q 2. Таким образом, имеем
. Поскольку а ≥ b, то q 1 ≥ q 2. Таким образом, имеем  , где
, где  . Следовательно,
. Следовательно,  .
.
Теорема 3. Если хотя бы один из множителей произведения делится на натуральное число b, то и все произведение делится на это число, то есть
 .
.
Доказательство. Пусть 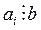 i = 1, 2,..., n, тогда существует
i = 1, 2,..., n, тогда существует  такое, что
такое, что  . Отсюда, используя коммутативный и ассоциативный законы умножения, можем записать:
. Отсюда, используя коммутативный и ассоциативный законы умножения, можем записать:  =
=  . Поскольку произведение
. Поскольку произведение 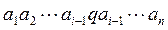 целых неотрицательных чисел является целым неотрицательным числом, то последнее равенство означает, что
целых неотрицательных чисел является целым неотрицательным числом, то последнее равенство означает, что 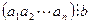 .
.
Теорема 4. Если в произведении ab множитель а делится на натуральное число m, а множитель b делится на натуральное число п, то произведение ab делится на произведение тп, то есть
 .
.
Доказательство. Пусть 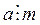 и
и 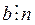 , тогда существуют
, тогда существуют  такие, что
такие, что 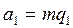 и
и  . Отсюда, на основании коммутативного и ассоциативного законов умножения, имеем ab = (mq 1)(nq 2) = (mn) (q 1 q 2) = (mn) q, где
. Отсюда, на основании коммутативного и ассоциативного законов умножения, имеем ab = (mq 1)(nq 2) = (mn) (q 1 q 2) = (mn) q, где  . Следовательно,
. Следовательно, 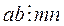 .
.
Теорема 5. Если в сумме одно слагаемое не делится на натуральное число b, а все остальные слагаемые делятся на это число, то и вся сумма на число b не делится.
Доказательство. Пусть 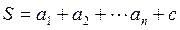 , где
, где  , но
, но  . Докажем, что
. Докажем, что 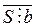 .
.
Предположим противное, то есть  . Тогда
. Тогда  , где
, где  и
и 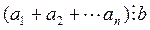 . По теореме 2 о делимости разности это означает, что
. По теореме 2 о делимости разности это означает, что 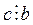 . Полученное противоречие и доказывает теорему.
. Полученное противоречие и доказывает теорему.
3. Иногда требуется установить, делится ли данное натуральное число а на натуральное число b, не производя самого деления. При этом оказываются полезными некоторые признаки.
Определение 2. Признаком делимости на число b называется правило, позволяющее по записи числа а ответить на вопрос о том, делится оно на b или нет, не производя самого деления.
Для вывода признаков делимости используем тот факт (см. теорему 1), что любое натуральное число х можно представить в виде
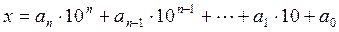 , (1)
, (1)
где 0 ≤ ai ≤ 9 (i = 0, 1,..., п), an ≠ 0.
Признак делимости на 2(5). Число х делится на 2(5) тогда и только тогда, когда на 2(5) делится число, образованное последней цифрой его десятичной записи:
 .
.
Доказательство необходимости. Пусть  . Поскольку
. Поскольку 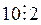 ,
, 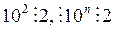 , то, по теоремам 3 и 1 о делимости произведения и суммы, можем утверждать, что в равенстве 1
, то, по теоремам 3 и 1 о делимости произведения и суммы, можем утверждать, что в равенстве 1  . Кроме того, по условию теоремы,
. Кроме того, по условию теоремы,  . Отсюда, по теореме 2 о делимости разности,
. Отсюда, по теореме 2 о делимости разности,  .
.
Доказательство достаточности. Пусть  . Поскольку
. Поскольку  , то, по теореме 1 о делимости суммы,
, то, по теореме 1 о делимости суммы,  .
.
Доказательство признака делимости на 5 не рассматриваем, поскольку оно проводится аналогично.
Признак делимости на 4(25). Число х делится на 4(25) тогда и только тогда, когда на 4(25) делится число, образованное двумя последними цифрами его десятичной записи:
 .
.
Доказательство необходимости. Пусть 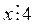 . Так как
. Так как 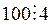 , то в равенстве (1) выражение
, то в равенстве (1) выражение 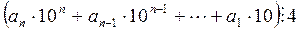 . Отсюда, по теореме о делимости разности,
. Отсюда, по теореме о делимости разности, 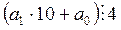 .
.
Доказательство достаточности. Пусть 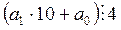 . Поскольку
. Поскольку 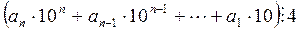 , то, по теореме о делимости суммы,
, то, по теореме о делимости суммы, 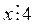 .
.
Доказательство признака делимости на 25 не приводим ввиду его аналогичности.
Признак делимости на 8(125). Число х делится на 8(125) тогда и только тогда, когда на 8(125) делится число, образованное тремя последними цифрами его десятичной записи.
 .
.
Доказательство проводится аналогично доказательству признаков делимости на 2 и 4 и рекомендуется читателю в качестве упражнения.
Признак делимости на 3(9). Число х делится на 3(9) тогда и только тогда, когда на 3(9) делится сумма однозначных чисел, образованных цифрами его десятичной записи:
 .
.
Доказательство необходимости. Заметим сначала, что все числа вида 10 n – 1, где  ,делятся на 3. Справедливость этого утверждения вытекает из равенства
,делятся на 3. Справедливость этого утверждения вытекает из равенства  .
.
Преобразуем число 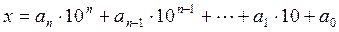 , прибавив и вычтя из него выражение
, прибавив и вычтя из него выражение  .
.
Тогда 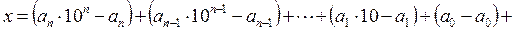
 .
.
После несложных преобразований можем записать равенство  .(2)
.(2)
По условию  . Кроме того, выражение
. Кроме того, выражение  , а значит, по теореме о делимости разности,
, а значит, по теореме о делимости разности,  .
.
Доказательство достаточности.
По условию,  . Так как
. Так как  , то, по теореме о делимости суммы, из равенства 2 следует, что
, то, по теореме о делимости суммы, из равенства 2 следует, что  . Аналогично доказывается признак делимости на 9.
. Аналогично доказывается признак делимости на 9.
Число признаков, приведенных выше, сравнительно невелико. На практике используется еще целый ряд признаков, обосновать которые мы сможем после рассмотрения соответствующего теоретического материала.
Лекция 2. Наибольший общий делитель и наименьшее общее кратное
План
1. Наибольший общий делитель и алгоритм Евклида.
2. Свойства наибольшего общего делителя.
3. Взаимно простые числа.
4. Наименьшее общее кратное.
Содержание
1. Если каждое из целых неотрицательных чисел а и b делится на число с, то число с называют общим делителем чисел. Чтобы найти общие делители чисел а и b, достаточно найти пересечение двух множеств: множества делителей числа а и множества делителей числа b. Это пересечение состоит из натуральных чисел, которые не могут превосходить меньшего из чисел а и b, а значит, в нем имеется наибольшее число. Это число называют наибольшим общим делителем чисел а и b.
Определение 3. Наибольшим общим делителем (НОД) чисел а и b называется самое большое натуральное число d, являющееся делителем для каждого из чисел а и b.
Наибольший общий делитель чисел а и b будем обозначать одним из символов – НОД(а; b)или (а; b).
Непосредственно из определения следует, что если хотя бы одно из чисел а и b отлично от нуля, то НОД(а; b) существует и является единственным. Возникает вопрос: как практически находить НОД?
Один из способов нахождения НОД вытекает непосредственно из определения 3. Действительно, можно было бы сначала найти все делители числа а, затем – числа b. После этого отобрать общие делители и выбрать из них наибольший. Такой путь, однако, был бы весьма нерациональным, особенно для больших чисел.
Другой, наиболее рациональный, способ нахождения НОД был предложен Евклидом (III в. до н.э.).
Теорема 6. Алгоритм Евклида. Если а разделить с остатком на b ≠ 0, затем разделить с остатком b на полученный остаток, затем разделить с остатком первый остаток на второй и т.д., то последний, отличный от нуля, остаток равен (а; b).
Доказательство. Проводя последовательно деления с остатком, указанные в формулировке теоремы, получим:
 |
(3)
Поскольку последовательность остатков является убывающей последовательностью целых неотрицательных чисел, то через конечное число шагов очередной остаток (например, rп +1) окажется равным нулю. Пусть rп – последний, отличный от нуля, остаток. Покажем, что rп = (а; b).
Прежде всего, докажем, что если а = bq + r, то (а; b) = (b; r).
Действительно, если  и
и  , то
, то 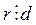 по теореме 2 о делимости разности. С другой стороны, если
по теореме 2 о делимости разности. С другой стороны, если  и
и 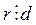 , то
, то  по теореме 1 о делимости суммы.
по теореме 1 о делимости суммы.
Таким образом, множества общих делителей чисел а и b равны, а значит, равны и их наибольшие общие делители, то есть (а; b) = (b; r).
Применяя доказанный факт к первому из равенств 3, получим
(а; b) = (b; r 1). (4)
Аналогично, из второго равенства последовательности (3)
(b; r 1) = (r 1; r 2). (5)
Продолжая аналогичныерассуждения, получим равенства:
 ; (6)
; (6)
 . (7)
. (7)
Исходя из равенств (4) – (7), можем записать: (а; b) = (b; r 1) = (r 1; r 2) =... = (rn- 2; rn- 1) = (rn- 1; rn) = (rn;0) = rn. Итак, (а; b) = rn. Теорема доказана.
Пример. Найти НОД(481; 703).
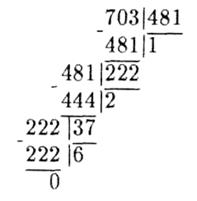 |
Мы определили и показали способ нахождения НОД двух чисел. Аналогично определяется НОД любого конечного множества целых неотрицательных чисел.
НОД чисел  обозначается одним из символов – НОД(
обозначается одним из символов – НОД( ) или (
) или ( ). Если
). Если 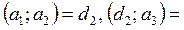
 , то (
, то ( ) = dn.
) = dn.
Пример. Найти НОД чисел 840, 720, 640 и 160.
1) НОД(840; 720) = 120;
2) НОД(120; 640) = 40;
3) НОД (40; 160) = 40.
Следовательно, НОД(840; 720; 640; 160) = 40.
2. Рассмотрим основные свойства НОД, выраженные следующими теоремами.
Теорема 7. НОД двух данных чисел делится на любой другой общий делитель этих чисел:
 .
.
Доказательство теоремы вытекает из алгоритма Евклида. Действительно, из первого равенства последовательности (3) следует, что если  и
и  , то
, то 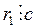 . Во втором равенстве
. Во втором равенстве  и
и 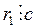 , а значит, и
, а значит, и 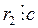 . Рассуждая аналогично, мы можем установить, что в правой части каждого из следующих равенств алгоритма вторые слагаемые должны делиться на с, то есть
. Рассуждая аналогично, мы можем установить, что в правой части каждого из следующих равенств алгоритма вторые слагаемые должны делиться на с, то есть 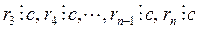 . Но rn = (а; b). Следовательно,
. Но rn = (а; b). Следовательно,  и теорема доказана.
и теорема доказана.
Теорема 8. Любой делитель НОД двух данных чисел является общим делителем этих чисел:
 .
.
Доказательство. Очевидно, что теорема 8 является обратной для теоремы 7. Пусть  . Докажем, что
. Докажем, что  и
и  .
.
По определениям делимости и НОД можем записать равенства:
 , где
, где  . (8)
. (8)
Кроме того, по условию теоремы, 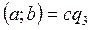 , где
, где 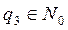 . Заменив в равенствах (8) НОД(а; b)произведением
. Заменив в равенствах (8) НОД(а; b)произведением 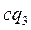 , получим равенства
, получим равенства  и
и 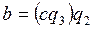 ,которые можно записать в виде
,которые можно записать в виде  ,
, 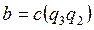 . Это означает, что
. Это означает, что  и
и  . Таким образом, теорема доказана.
. Таким образом, теорема доказана.
Теорема 9. Если каждое из двух данных чисел умножить на натуральное число, то НОД этих чисел умножится на то же число:
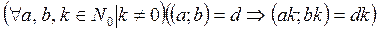 .
.
Доказательство. Пользуясь свойством монотонности умножения, умножим обе части каждого из равенств (3) на одно и то же число k. В полученных равенствах вместо натуральных чисел
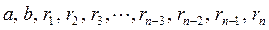
будут, соответственно, стоять новые числа:
 .
.
Значит, (ak; bk) = rnk, или (ak; bk)= dk,что и требовалось доказать.
Теорема 10. Если каждое из двух данных чисел разделить на натуральное число, то НОД этих чисел разделится на то же число:
 .
.
Доказательство. Поскольку данная теорема является обратной теореме 9, то для ее доказательства достаточно к последовательности равенств (3) алгоритма Евклида применить преобразования обратные тем, что были проведены в теореме 9.
3. Во многих вопросах теории делимости используются числа, не имеющие общих делителей, кроме единицы. Рассмотрим такие числа более подробно.
Определение 4. Если НОД чисел равен единице, то числа называются взаимно простыми.
 – взаимно просты
– взаимно просты  .
.
Если  – совокупность взаимно простых чисел, то отсюда не следует, что любые подмножества этой совокупности взаимно просты.
– совокупность взаимно простых чисел, то отсюда не следует, что любые подмножества этой совокупности взаимно просты.
Пример. Так, (35; 55; 77) = 1, но (35; 55) = 5, (55; 77) = 11, (35; 77) = 7.
Теорема 11. Если данные числа разделить на их НОД, то полученные частные будут числами взаимно простыми:
 .
.
Следует заметить, что символы  и
и  здесь представляют натуральные числа.
здесь представляют натуральные числа.
Справедливость теоремы 11 вытекает из теоремы 10. Действительно, если каждое из чисел а и b разделить на натуральное число d, то и НОД этих чисел разделится на d, а значит, будет равен 1.
Теорема 12. Если произведение двух чисел делится на число, взаимно простое с одним из множителей, то другой множитель делится на это число:

Доказательство. По условию теоремы, (а; с) = 1. Пользуясь теоремой 9, умножим каждое из чисел а и с на число b. Тогда НОД этих чисел также умножится на b, то есть (аb; сb) = b. По условию теоремы,  . Кроме того, очевидно, что
. Кроме того, очевидно, что  . Следовательно, с является общим делителем чисел ab и сb. Но тогда, по теореме 7, НОД этих чисел также делится на с, то есть
. Следовательно, с является общим делителем чисел ab и сb. Но тогда, по теореме 7, НОД этих чисел также делится на с, то есть  .
.
Теорема 13. (Признак делимости на составное число.) Если числа а и b взаимно просты, то число с делится на их произведение ab тогда и только тогда, когда с делится на а и на b:
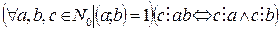 .
.
Доказательство. Необходимость вытекает из транзитивности отношения делимости. Так как 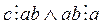 , то
, то  . Аналогично, из условия
. Аналогично, из условия 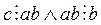 b следует, что
b следует, что  .
.
Достаточность. Пусть  и
и  , причем (а; b) = 1. Докажем, что
, причем (а; b) = 1. Докажем, что  . Так как
. Так как  , то с = aq 1, где
, то с = aq 1, где  . Зная, что
. Зная, что  , имеем
, имеем 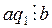 , где (а; b) = 1. По теореме 12 это означает, что
, где (а; b) = 1. По теореме 12 это означает, что 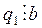 , то есть q l = bq 2, где
, то есть q l = bq 2, где 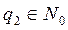 . Итак, с = aq 1 = a (bq 2) = (ab) q 2, то есть
. Итак, с = aq 1 = a (bq 2) = (ab) q 2, то есть  . Теорема полностью доказана.
. Теорема полностью доказана.
Из этой теоремы вытекает ряд признаков делимости на числа, каждое из которых является произведением двух взаимно простых чисел. Например:
1. Число х делится на 6 тогда и только тогда, когда оно делится на 2 и 3.
2. Число х делится на 36 тогда и только тогда, когда оно делится на 4 и 9.
Аналогично формулируются признаки делимости на числа 12, 15, 18, 24, 45 и др.
4. Пусть а и b – произвольные натуральные числа. Натуральное число m называется общим кратным этих чисел, если m делится на каждое из чисел а и b. Если m – общее кратное чисел а и b,то, по транзитивности отношения делимости, каждое из чисел 2 m, 3 m, 4 m,... также является общим кратным чисел а и b. Среди натуральных общих кратных, по принципу наименьшего числа, существует наименьшее общее кратное.
Определение 5. Наименьшим общим кратным (НОК) чисел а и b называется наименьшее натуральное число т, являющееся общим кратным этих чисел.
Наименьшее общее кратное чисел а и b будем обозначать одним из символов – НОК(а; b) или[ а; b ].
Примечание. Нуль, как известно, является общим кратным для любых натуральных чисел, но, по определению, НОК(а; b) > 0.
Теорема 14. Любое общее кратное двух чисел делится на их наименьшее общее кратное.
Доказательство теоремы проведем методом от противного. Пусть с – произвольное общее кратное чисел а и b, т = [ а; b ]. Предположим, что с не делится нацело на m. Тогда, разделив
с на m с остатком, получим с = mq + r, 0 ≤ r < m. Поскольку
с кратно а и b, mq кратно а и b, то, по теореме 2 о делимости разности, r кратно а и b. Но это противоречит тому, что m является НОК, ибо r < m. Полученное противоречие доказывает теорему.
Докажем теперь теорему, устанавливающую связь НОД и HОК двух чисел. Эта теорема дает практический способ нахождения НОК двух чисел.
Теорема 15. НОК и НОД двух натуральных чисел а и b связаны соотношением
аb = (а; b) · [ а; b ].
Доказательство. По определению НОД можем записать равенства а = (а; b) а 1, b = (а; b) b 1. Тогда
 и
и  .
.
Из последних равенств следует, что число  является общим кратным чисел а и b, а значит, по теореме 14, оно делится на [ а; b ].
является общим кратным чисел а и b, а значит, по теореме 14, оно делится на [ а; b ].
Следовательно, можем записать:
 . (9)
. (9)
Докажем теперь, что последнее равенство возможно только при q = 1.
По определению НОК можем записать: [ а; b ] = aq 1и [ а; b ] = bq 2. Подставляя новые выражения НОК в равенство (9), получим
 и
и 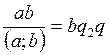 .
.
Из последних равенств, в свою очередь, имеем
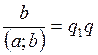 и
и  .
.
Отсюда 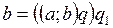 и
и  . Таким образом, выражение (а; b) q является общим делителем чисел а и b. Но это возможно только при q = 1.
. Таким образом, выражение (а; b) q является общим делителем чисел а и b. Но это возможно только при q = 1.
Итак, равенство (9) можем переписать в виде
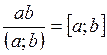 , или ab = (а; b) [ а; b ]
, или ab = (а; b) [ а; b ]
Теорема доказана.
Следствие. НОК двух взаимно простых чисел равно их произведению.
Пример. Найти НОК чисел 315 и 126.
НОК(315; 126) =  .
.
Мы рассмотрели определение и способ нахождения НОК двух чисел. Аналогично определяется НОК любого конечного множества чисел. НОК чисел  обозначают [
обозначают [  ] и находят по следующему правилу: сначала находят [ а 1; а 2] = m 2, затем – [ m 2; a 3] = m 3, [ m 3; a 4] = m 4, …, [ mn- 1; an ] = mn. Тогда [ a 1; a 2;...; an ] =mn.
] и находят по следующему правилу: сначала находят [ а 1; а 2] = m 2, затем – [ m 2; a 3] = m 3, [ m 3; a 4] = m 4, …, [ mn- 1; an ] = mn. Тогда [ a 1; a 2;...; an ] =mn.
Пример. Найти НОК чисел 30, 120, 72 и 64.
1) НОК(30; 120) = 120;
2) НОК(120; 72) =  ;
;
3) НОК(360;64) =  .
.
Следовательно, НОК(30; 120; 72; 64) = 2880.
Лекция 3. Простые и составные числа
План
1. Простые числа.
2. Распределение простых чисел в натуральном ряду.
3. Разложение чисел на простые множители.
Содержание
1. Каждое натуральное число р ≠ 1 имеет по крайней мере два делителя: 1 и p.
Определение 6. Натуральное число р ≥ 1 называется простым, если оно не имеет делителей, отличных от 1 и р.
Например, числа 7, 13, 19 являются простыми, так как каждое из них делится только само на себя и на единицу.
Определение 7. Натуральное число п ≥ 1 называется составным, если оно имеет более двух делителей.
Например, 12 – составное число, так как имеет делители: 1, 2, 3, 4, 6, 12.
Таким образом, по числу натуральных делителей множество N натуральных чисел разбивается на три непересекающихся класса:
I кл. – число 1 (один делитель);
II кл. – простые числа (два делителя);
III кл. – составные числа (более двух делителей).
Известно, что нуль делится на любое натуральное число, то есть имеет бесконечно много делителей. Поэтому множество N0 целых неотрицательных чисел по числу натуральных делителей разбивают на четыре непересекающихся класса. К трем вышеуказанным классам добавляется
IV кл. – число 0 (бесконечно много делителей).
Теорема 16. (О существовании простого делителя.)Если
d ≠ 1 – наименьший делитель натурального числа n > 1, то d – простое число.
Доказательство. Будем рассуждать методом от противного. Предположим, что d – составное число. Тогда, по определению 7, d делится на 1, d и некоторое число t, где 1 < t < d. Следовательно, имеем  и
и  , а по транзитивности отношения делимости это означает, что
, а по транзитивности отношения делимости это означает, что 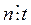 . Получили противоречие с тем, что d – наименьший делитель числа п. Тем самым теорема доказана.
. Получили противоречие с тем, что d – наименьший делитель числа п. Тем самым теорема доказана.
Один из первых вопросов, который возникает в связи с простыми числами, это вопрос о том, конечно или бесконечно множество простых чисел. Ответ на этот вопрос дает следующая теорема, доказанная еще Евклидом в 9-ой книге его знаменитых «Начал».
Теорема 17. Множество простых чисел бесконечно.
Доказательство. Проведем доказательство методом от противного. Предположим, что множество простых чисел конечно. Тогда элементы его можно занумеровать числами отрезка натурального ряда. Пусть 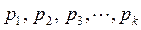 – все простые числа и других простых чисел нет. Рассмотрим число
– все простые числа и других простых чисел нет. Рассмотрим число
 .
.
Число п является натуральным и, значит, должно принадлежать одному из трех вышеупомянутых классов. Но  I кл., так как п > 1;
I кл., так как п > 1;  II кл., так как п больше любого простого числа pi (i = 1, 2,..., k). Остается предположить, что
II кл., так как п больше любого простого числа pi (i = 1, 2,..., k). Остается предположить, что  III кл., то есть n – составное число. Тогда, по теореме 16, п должно делиться хотя бы на одно из простых чисел pi (i = 1, 2,..., k). Пусть
III кл., то есть n – составное число. Тогда, по теореме 16, п должно делиться хотя бы на одно из простых чисел pi (i = 1, 2,..., k). Пусть  , 1 ≤ s ≤ k. Рассматривая равенство (10) замечаем, что в нем
, 1 ≤ s ≤ k. Рассматривая равенство (10) замечаем, что в нем  ,
,  , а значит, по теореме 2 о делимости разности,
, а значит, по теореме 2 о делимости разности, 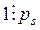 ,что невозможно. Полученное противоречи
,что невозможно. Полученное противоречи