Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное
Образовательное учреждение высшего образования
«тюменский ИНДУСТРИАЛЬНый университет»
Институт геологии и нефтегазодобычи
Кафедра «Геологии месторождений нефти и газа»
Математические методы
Моделирования в геологии
Методические указания
для лабораторных и самостоятельных занятий
студентов специальностей 21.05.02 «Прикладная геология»,
всех форм обучения
В. А. Белкина, Н.В. Санькова
Тюмень
ТюмГИУ
УДК 519.2
Белкина В.А. Математические методы моделирования в геологии [Текст]: Методические указания для лабораторных и самостоятельных работ / сост. В.А. Белкина, Н.В. Санькова – Тюмень: ТюмГИУ 2016.– 40 с.
Методические указания для лабораторных и самостоятельных работ рассмотрены и рекомендованы к изданию методическим семинаром кафедры «Геологии месторождений нефти и газа»
«04» апреля 2016 года, протокол № 7
Аннотация
Методические указания «Математические методы моделирования в геологии» предназначены для студентов, обучающихся по специальности 21.05.02 «Прикладная геология» всех форм обучения при изучении по дисциплины «Математические методы моделирования в геологии». Указанная дисциплина изучается в одном семестре.
В методических указаниях «Математические методы моделирования в геологии» приведено содержание основных тем дисциплины, указан перечень лабораторных работ. Даны методические указания по выполнению лабораторных работ.
© Федеральное государственное
бюджетное образовательное учреждение высшего образования
«Тюменский индустриальный
университет», 2016 г.
ВВЕДЕНИЕ
Высокие темпы развития нефтяной и газовой промышленности в Западной Сибири обуславливают необходимость ускоренного изучения геологического строения нефтяных залежей с целью сокращения сроков разведки и введения их в разработку. Все это требует оперативной обработки большого объема информации, что немыслимо без использования ЭВМ и математических методов.
С другой стороны, довольно богатый геологический материал, накопленный к настоящему времени, позволяет обработку полевых (эмпирических) данных вести в более сложных геологических моделях с большим числом параметров. В процессе геологической интерпретации все чаще привлекаются процедуры моделирования, применение которых невозможно без привлечения методов математической статистики и ЭВМ. Все это предъявляет довольно серьезные требования к математической подготовке будущих геологов, в частности, грамотному применению математических методов обработки и интерпретации результатов измерений.
В методическом указании рассматриваются методы статистической обработки наблюдений над отдельными признаками геологических объектов (задания 1-2) и методы изучения взаимосвязей между двумя признаками (задания 3-5). Для каждой работы подробно описан порядок её выполнения. Выполненные работы сдаются в электронном виде в соответствии с пунктами порядка выполнения работы.
В результате изучения дисциплины студент должен знать методы статистического анализа эмпирических данных и уметь использовать эти методы при решении геологических задач.
ПРАВИЛА ТЕХНИКИ БЕЗОПАСНОСТИ ПРИ
ПРОВЕДЕНИИ ЛАБОРАТОРНЫХ И САМОСТОЯТЕЛЬНЫХ РАБОТ
Оборудование. Лабораторные и самостоятельные работы выполняются на персональных компьютерах в среде программного комплекса Excel.
К выполнению лабораторных работ допускаются студенты, изучившие настоящие правила по технике безопасной работы на ПК, а также прошедшие инструктаж по технике безопасности на рабочем месте.
Во время работы в компьютерном классе запрещается:
- включать без разрешения оборудование;
- трогать разъемы соединительных кабелей и проводов (возможно поражение электрическим током);
- прикасаться к питающим проводам и устройствам заземления;
- прикасаться к экрану и к тыльной стороне монитора, клавиатуры;
- включать и выключать аппаратуру без указания преподавателя;
- работать в верхней одежде и влажными руками;
- находиться во время перемены в компьютерном классе без разрешения преподавателя;
- класть диски, книги, тетради и другие предметы на монитор и клавиатуру;
- устанавливать или копировать программы с дискет, дисков и флеш-носителей на компьютер, предварительно не проверив их антивирусом.
Во время работы в компьютерном классе:
- следите за исправностью аппаратуры и немедленно прекращайте работу при появлении необычного звука или самопроизвольного отключения аппаратуры;
- легко и быстро нажимайте на клавиши, не допуская резких ударов;
- не пользуйтесь клавиатурой и мышью, если не включен компьютер;
- работайте на клавиатуре чистыми руками;
- не пытайтесь самостоятельно устранить неисправность аппаратуры;
- при появлении запаха гари немедленно прекратите работу, выключите аппаратуру и сообщите об этом преподавателю.
Задание 1. Описание геологических объектов
1.1 Цель работы
Овладеть навыками нахождения точечных оценок статистических характеристик и построения гистограмм геологических и геофизических параметров.
1.2 Основные теоретические положения
Полное статистическое описание случайных величин дают функции распределения F(х) и плотности вероятностей Р(х). Но при решении ряда задач можно ограничиться параметрами распределений: математическим ожиданием a, дисперсией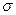 
2 (или средним квадратичным отклонением 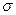), асимметрией, эксцессом и т. д. Все перечисленные функции и параметры – понятия теоретические.
При статистическом анализе геологических признаков по наблюденным значениям находят оценки (приближенные значения) функций F(х) или Р(х) и параметров a, 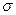2.
Для получения оценки функции Р(х), наблюденные значения какого-либо параметра Х (варианты) вначале сортируют по возрастанию и находят максимальную и минимальную варианты. Затем интервал, в котором лежат все замеренные значения Х, делят на более мелкие, частичные интервалы Dхi, число которых принимается не больше 20-25. И, наконец, определяется количество значений случайной величины Х, попавших в каждый i-ый частичный интервал ni. Обозначим за N – число всех измерений Х, тогда имеет место: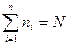 
. Величины ni называются частотами. Отношения: 
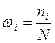называются относительными частотами. Они могут быть выражены в процентах: wi= 
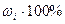. Величины wi показывают, какой процент измерений из общего объема наблюдений лежит в i-ом частичном интервале.
По выбору частичных интервалов сделаем следующие замечания. Лучше всего их принимать равными, так как только в этом случае лучше всего выявляется закономерность изменения частот с изменением значений Х. Кроме того, при неравных Dхi =1, 2,… применение многих более глубоких статистических приемов оказывается невозможным. Длину частичного интервала Dх следует брать с учетом объема измерений N, характера изменения частот и решаемых задач. Если окажется, что частоты соседних интервалов весьма значительно отличаются одна от другой, следует увеличить величину Dх.
Для придания построенным рядам более наглядного вида применяют их графическое изображение в виде гистограмм. Гистограммой частот называют ступенчатый график, на котором по оси абсцисс отложены частичные интервалы, а по оси ординат – соответствующие ni или wi. Плотностью частоты рni (или частости р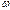 
i) называют отношение частоты ni (или частости 
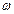i) к длине частичного интервала: рni= ni /Dх.
Построенные таблицы и графики дают первое представление о форме законов распределения. Следующая задача более глубокого изучения случайных величин основана на оценке параметров распределений. Одной из оценок математического ожидания является среднее арифметическое, определяемое по формуле: 
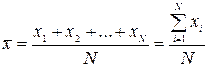. (1.1)
В качестве оценки дисперсии используется среднее арифметическое квадратов отклонений значений хi, i=1, 2,…, N от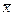 
:
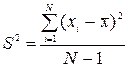. (1.2)
Среднее квадратичное отклонение S равно корню квадратному из дисперсии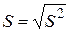 
.
1.3 Пример. Имеются данные искажений (помехи) годографов преломленных волн (мс), полученные в Пуровском районе
-6 -27 -14 -5 -2 7 0 -26 -13 -9 4 8 16 20 23 -10 -1 -7 7 5
-8 14 18 12 -17 0 -4 2 12 5 -9 -14 -16 -10 2 3 9 8 -2 1
-2 5 -9 -12 -10 2 3 5 2 9 5 10 9 1 2 9 -4 -8 -3 -6
-2 -6 -8 -2 3 8 -1 -12 -15 2 3 0 2 4 5 7 11 16 2 4
1 -2 -6 -9 -7 -6 -3 -6 -9 -2 6 13 10 7 9 -18 -1 1 -2 -5
Оценить параметры распределения: математическое ожидание, дисперсию и построить гистограмму, на которую нанести теоретическую кривую плотности нормального распределения с найденными оценками параметров распределения.
Статистическое описание начинается с нахождения минимальной и максимальной вариант, в рассматриваемом примере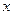 
min=-27, 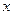max=23. Затем исходная выборка группируется в интервальную таблицу (табл. 1.1). Для этого вычисляется размах варьирования R = xmax- xmin, который делится на выбранное число интервалов k (k =10), длина каждого интервала Dх=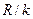 
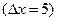округляется до ближайшего наибольшего целого числа. Затем находится число вариант в каждом интервале (табл. 1.1). На основе этой таблицы частот построена гистограмма (рис. 1.1).
Затем, по формулам (1.1) и (1.2) найдены точечные оценки параметров распределения: 
, 
, 
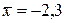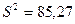. Полученные значения хорошо согласуются с гистограммой.
Для нахождения значений функции плотности нормального распределения с параметрам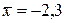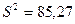и , и надо сделать следующее:
1. найти центры частичных интервалов по формуле:
хiц = (хi + хi+1)/2;
2. вычислить значения функции плотности нормального распределения в точках хiц по формуле:
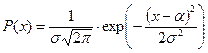
3. найденные значения yi умножить на Dх (для проверки найти сумму значений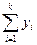 
, она должна не значимо отличаться от 1, в противном случае в предыдущих расчётах имеются ошибки);
4. на построенную гистограмму нанести второй ряд данных (вычисленный в пункте 3) и изменить тип диаграммы.
Таблица 1.1
| Границы интервалов | Частоты | Границы Интервалов | Частоты | Границы Интервалов | Частоты |
| -27, -22 -22, -17 -17, -12 | -12, -7 -7, -2 -2, 3 | 3, 8 8, 13 13, 18 18, 23 |
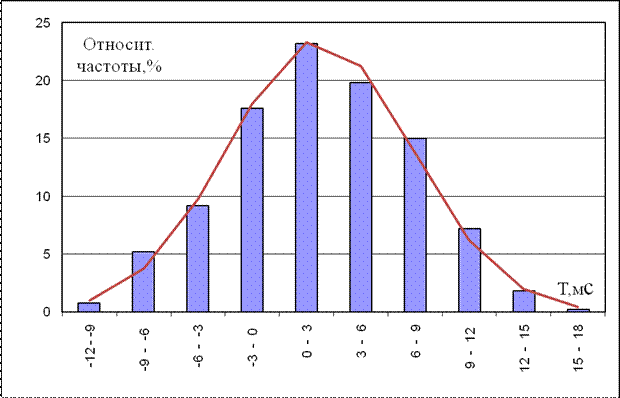
Рис. 1.1 Гистограмма относительных частот
1.5 Порядок выполнения заданий
1. С помощью датчиков случайных чисел сформировать выборочные совокупности объемом 1000 случайных чисел с параметрами распределений, приведенными в табл. 1.2. Сгенерировать три выборки с распределениями:
- нормальное,
- равномерное,
- Пуассоновское.
2. Вычислить значения x, S, S2 для каждой выборки (формулы 1.1, 1.2).
3. Построить гистограммы вышеуказанных случайных величин с наложением на них кривой распределения частот нормальной случайной величины, среднее значение и дисперсия которой определяется по выборке.
Замечание. При расчетах в Exсel результаты каждой случайной величины помещать на отдельном листе.
Варианты заданий
Варианты заданий приведены в табл. 1.2.
Таблица 1.2
Параметры распределений случайных величин
| № п/п | Нормальное | Равномерное | Пуассона | |
| Среднее значение | Стандартное отклонение | Интервал | Лямбда | |
| 0-12 | ||||
| 3,5 | 0-14 | |||
| 0-16 | ||||
| 4,5 | 0-18 | |||
| 0-20 | ||||
| 5,5 | 0-22 | |||
| 0-24 | ||||
| 6,5 | 0-26 | |||
| 0-28 | ||||
| 7,5 | 0-30 | |||
| 0-32 | ||||
| 8,5 | 0-34 | |||
| 0-36 | ||||
| 9,5 | 0-38 | |||
| 0-40 | ||||
| 5-15 | ||||
| 1-15 | ||||
| 4-16 | ||||
| 2-16 | ||||
| 3-18 | ||||
| 2-14 | ||||
| 1-17 | ||||
| 3-16 | ||||
| 4-20 | ||||
| 3-17 | ||||
| 3-19 | ||||
| 2-17 | ||||
| 3-19 | ||||
| 2-20 | ||||
| 3-21 |
1.6 Вопросы для самопроверки знаний
по лабораторной работе №1
1. Дать определение генеральной совокупности.
2. Дать определение выборочной совокупности.
3. Сформулировать алгоритм построения гистограммы.
4. Дать определение частоты, относительной частоты.
5. По какой формуле находится оценка математического ожидания нормально распределённой случайной величины?
6. По какой формуле находится оценка дисперсии нормально распределённой случайной величины?
7. Что называется модой и медианой вариационного ряда?
8. Назовите основные свойства нормального распределения.
9. Дать определение размаха варьирования.
10. Какими двумя статистическими характеристиками определяется нормальное распределение?
11. Какое распределение называется равномерным?
Задание 2. сравнение геологических объектов
2.1 Цель работы
Научиться методами математической статистики сравнивать средние и дисперсии геологических и геофизических признаков с целью выяснения случайности или неслучайности их различия.
2.2 Основные теоретические положения
В геологической практике часто возникает необходимость сравнения средних и дисперсий признаков с целью выяснения случайности или неслучайности их различия. Задачи такого рода решаются путём проверки статистических гипотез.
Гипотеза о равенстве дисперсий двух нормальных генеральных совокупностей: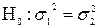 
при конкурирующей гипотезе: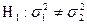 
проверяется с помощью критерия
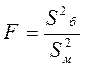. (2.1)
В условиях нулевой гипотезы величина F имеет распределение Фишера - Снедекора со степенями свободы k1=N1-1 и k2=N2-1, где N1–объем выборки, с большей дисперсией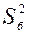 
, N2 – объем выборки с меньшей дисперсией 
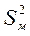. Обозначим значение критерия, вычисленное по данным наблюдений, через Fнабл. По таблице критических точек распределения Фишера-Снедекора (приложение 2) для уровня значимости 
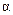/2 (вдвое меньше заданного) и числа степеней свободы k1 и k2 необходимо найти критическую точку Fкр( 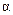/2, k1, k2). Если Fнабл.< Fкр( 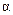/2, k1, k2), то нет основания отвергнуть нулевую гипотезу. Если Fнабл.>Fкр( 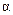/2, k1, k2) - нулевую гипотезу отвергают, другими словами, дисперсии нормальных генеральных совокупностей различаются значимо.
Гипотеза о равенстве двух средних для нормальных генеральных совокупностей, дисперсии которых неизвестны и, предположительно, одинаковы: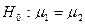 
при конкурирующей гипотезе: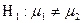 
проверяется с помощью критерия:
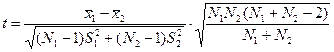, (2.2)
где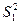 
, 
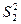- выборочные дисперси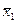и, 
и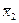 
- выборочные средние, найденные по независимым малым выборкам объема N1 и N2 соответственно.
В условиях нулевой гипотезы величина t имеет распределение Стьюдента с k=N1+N2-2 степенями свободы. Обозначим значение критерия, вычисленное по данным наблюдений, через tнабл. По таблице критических точек распределения Стьюдента (приложение 1) для заданного уровня значимости a и числа степеней свободы k необходимо найти критическую точку tкр(a; k). Если |tнабл.| < tкр(a; k) – отвергнуть нулевую гипотезу нет оснований. Если |tнабл.| > tкр(a; k) – нулевую гипотезу отвергают, другими словами, выборочные средние нормальных генеральных совокупностей различаются значимо.
2.3 Пример. Показать случайно или закономерно наблюдаемое различие средних значений глубин залегания (в м) подошвы соленосного комплекса Кунгура в Прикаспийской синеклизе по данным бурения и сейсморазведки (табл. 2.1).
Таблица 2.1
| Данные бурения | |||||||||
| Данные МОВ |
| Данные бурения | ||||||||||||
| Данные МОВ |
Решение: 1. Вычислим оценки средних и дисперсий по формулам (1.1) и (1.2):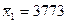 
; 
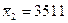м.; 
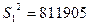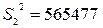м2; 
м2.
2. Проверим нулевую гипотезу о равенстве генеральных дисперсий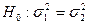 
. По формуле 2.1 вычислим Fнабл. Fнабл = 811905:565477=1,44. Зададимся уровнем значимости a=0,1, достаточным для решения практических задач геологии и по таблице приложения 2 при степенях свободы k1=21-1=20 и k2=21-1=20 найдем критическую точку Fкр(0,05; 20; 20)»2,13. Таким образом, с вероятностью 90 % различие дисперсий изучаемых совокупностей несущественно.
3. Сравним генеральные средние, проверив гипотезу 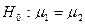. По формуле 2.2 вычислим t набл: t набл »0,97. По таблице приложения 1 для уровня значимости a=0,1 и числа степеней свободы k=21+21-2=40 найдем критическую точку tкр(0,1; 40)=1,68. Так как |tнабл| < tкр – отвергнуть нулевую гипотезу о равенстве генеральных средних нет оснований, другими словами, средние генеральных выборок различаются незначимо. Таким образом, с доверительной вероятностью 90% на современной стадии изученности средние значения глубин по данным бурения и сейсморазведки совпадают. Следовательно, наблюдаемые в таблице 2.1 различия глубин залегания подошвы соленосного комплекса кунгура в Прикаспийской синеклизе по данным бурения и сейсморазведки носят случайный характер.
2.4. Порядок выполнения задания
1. Привести полный текст варианта (данные приведены в табл. 2.2).
2. Вычислить выборочные средние и исправленные выборочные дисперсии и средние квадратичные отклонения.
3. Проверить нулевую гипотезу о равенстве генеральных дисперсий: вычислить Fнабл. по формуле 2.1, определить Fкр по таблице приложения 2, сравнить Fнабл. и Fкр и написать вывод.
4. Проверить нулевую гипотезу о равенстве двух средних нормальных генеральных совокупностей: вычислить tнабл. по формуле 2.2, определить tкр по таблице приложения 1, сравнить |tнабл.| и tкр.
5. Написать выводы о случайном или закономерном различии коллекторских свойств пород выбранных интервалов разреза скважины 3 Карайской площади.
2.5 Варианты
Показать, случайно или закономерно наблюдаемое различие в коллекторских свойствах пород выбранных интервалов разреза скважины 3 Карайской площади (данные приведены в табл. 2.2).
а) Сравнить значения открытой пористости в следующих интервалах пласта:
1. 2809,6-2816,6 и 2816,6-2839,8
2. 2809,6-2816,6 и 2839,8-2858,0
3. 2816,6-2839,8 и 2839,8-2858,0
4. 3001,2-3040,8 и 3040,8-3050,0
5. 3001,2-3040,8 и 3163,0-3173,0
6. 3040,8-3050,0 и 3163,0-3173,0
7. 2809,6-2816,6 и 3001,2-3040,8
8. 2839,8-2858,0 и 3001,2-3040,8
9. 2816,6-2839,8 и 3040,8-3050,0
10. 2816,6-2839,8 и 3001,2-3040,8
11. 2809,6-2816,6 и 3163,0-3173,0
12. 2839,8-2858,0 и 3040,8-3050,0
13. 2839,8-2858,0 и 3163,0-3173,0
б) Сравнить значения остаточной воды
в следующих интервалах пласта:
14. 2809,6-2816,6 и 3163,0-3173,0
15. 2809,6-2816,6 и 2816,6-2839,8
16. 2816,6-2839,8 и 3040,8-3050,0
17. 2809,6-2816,6 и 2839,8-2858,0
18. 3001,2-3040,8 и 3040,8-3050,0
19. 3001,2-3040,8 и 3163,0-3173,0
20. 3040,8-3050,0 и 3163,0-3173,0
21. 2809,6-2816,6 и 3040,8-3050,0
22. 2816,6-2839,8 и 2839,8-2858,0
23. 2839,8-2858,0 и 3001,2-3040,8
24. 2809,6-2816,6 и 3163,0-3173,0
25. 2839,8-2858,0 и 3040,8-3050,0
26. 2839,8-2858,0 и 3163,0-3173,0
Таблица 2.2
Скважина 3 Карайской площади
| Интервал пласта | Открытая пористость | Остаточ. вода | Интервал пласта | Открытая пористость | Остаточ. вода |
| 2809,6-2816,6 | 13,4 | 55,4 | 3001,2-3012,5 | 6,3 | 79,3 |
| -“- | 12,3 | 44,1 | -“- | 9,7 | 75,7 |
| -“- | 15,0 | 62,5 | -“- | 4,2 | 78,7 |
| -“- | 18,1 | 34,4 | -“- | 2,3 | 81,2 |
| -“- | 8,8 | 71,2 | -“- | 4,2 | 82,0 |
| -“- | 9,7 | 75,3 | -“- | 5,2 | 76,6 |
| -“- | 17,9 | 35,4 | -“- | 8,9 | 88,2 |
| -“- | 17,1 | 35,6 | 3027,0-3040,8 | 7,6 | 79,8 |
| -“- | 14,3 | 34,8 | -“- | 5,4 | 77,9 |
| -“- | 17,7 | 33,1 | -“- | 12,8 | 60,2 |
| -“- | 13,8 | 34,1 | -“- | 12,4 | 67,4 |
| -“- | 11,0 | 74,4 | -“- | 8,6 | 79,2 |
| -“- | 7,7 | 85,5 | -“- | 11,0 | 64,9 |
| -“- | 12,9 | 67,5 | -“- | 8,0 | 71,9 |
| -“- | 12,2 | 77,1 | -“- | 5,2 | 76,7 |
| -“- | 11,3 | 83,1 | -“- | 4,8 | 73,3 |
| -“- | 12,2 | 78,4 | -“- | 4,5 | 77,5 |
| 2816,6-2839,8 | 9,4 | 85,0 | -“- | 4,7 | 78,0 |
| -“- | 5,9 | 90,1 | -“- | 3,3 | 78,8 |
| -“- | 7,7 | 68,4 | -“- | 9,1 | 72,0 |
| -“- | 4,4 | 77,6 | -“- | 7,0 | 81,7 |
| -“- | 13,5 | 64,6 | -“- | 10,8 | 77,4 |
| -“- | 10,7 | 79,0 | -“- | 10,1 | 75,6 |
| -“- | 12,6 | 78,8 | -“- | 9,2 | 81,6 |
| -“- | 15,6 | 51,6 | -“- | 9,7 | 80,0 |
| -“- | 12,6 | 58,7 | -“- | 8,7 | 75,5 |
| -“- | 15,4 | 38,8 | -“- | 9,8 | 79,3 |
| -“- | 13,6 | 47,8 | 3040,8-3050,0 | 10,2 | 65,5 |
| -“- | 12,8 | 50,9 | -“- | 10,2 | 67,2 |
| -“- | 14,7 | 46,3 | -“- | 8,9 | 66,5 |
| 2839,8-2858,0 | 16,8 | 40,6 | -“- | 11,2 | 72,7 |
| -“- | 16,3 | 39,9 | -“- | 7,9 | 76,5 |
| -“- | 16,4 | 42,8 | -“- | 10,5 | 70,3 |
| -“- | 16,4 | 43,6 | -“- | 8,9 | 80,8 |
| -“- | 16,8 | 43,9 | -“- | 9,5 | 73,3 |
| -“- | 13,2 | 47,3 | -“- | 3,8 | 79,0 |
| -“- | 13,8 | 44,9 | -“- | 6,8 | 78,8 |
| -“- | 15,8 | 46,3 | -“- | 10,3 | 64,0 |
| -“- | 17,3 | 43,0 | -“- | 10,0 | 77,4 |
| -“- | 12,9 | 50,0 | 3163,0-3173,0 | 5,5 | 86,0 |
| -“- | 14,5 | 57,5 | -“- | 5,2 | 73,5 |
| -“- | 15,1 | -“- | 5,3 | 72,1 | |
| -“- | 15,4 | -“- | 5,9 | 76,0 | |
| -“- | 12,3 | 69,6 | -“- | 6,5 | 80,9 |
| -“- | 14,8 | 59,4 | -“- | 6,5 | 79,5 |
| -“- | 14,5 | 62,6 | -“- | 6,7 | 87,1 |
| -“- | 14,6 | 59,8 | -“- | 5,4 | 83,7 |
| -“- | 14,7 | 70,4 | -“- | 4,9 | 79,9 |
| -“- | 11,7 | 58,2 | -“- | 3,7 | 81,7 |
2.6 Вопросы для самопроверки знаний
по лабораторной работе №2
1. Дать определение статистической гипотезы.
2. Что называется статистическим критерием?
3. Сформулировать алгоритм применения любого статистического критерия для обработки экспериментальных данных.
4. Сформулировать правило применения критерия Фишера для проверки гипотезы о равенстве дисперсий двух нормальных генеральных совокупностей.
5. Сформулировать правило применения критерия Стьюдента для проверки гипотезы о равенстве средних значений двух нормальных генеральных совокупностей.
6. Какое распределение имеет величина F в критерии Фишера?
7. Какая статистическая характеристика описывает разброс точек вокруг математического ожидания?
8. Какое распределение имеет величина t в критерии Стьюдента?
9. Что называется уровнем значимости?
Задание 3. Количественная оценка тесноты
линейной связи между геологическими объектами
3.1 Цель работы
Научиться решать задачу определения тесноты линейной статистической зависимости между геологическими и петрофизическими параметрами.
3.2 Основные теоретические положения
Зависимости между величинами или явлениями могут быть двух видов: функциональные и статистические. Строгая функциональная зависимость между геологическими признаками практически никогда не реализуется, так как все параметры в геологии отягощены случайными ошибками. Последние слагаются из инструментальных ошибок, ошибок из-за приближенности модели, существенной неоднородности геологических объектов и т. д. Статистическая зависимость, в частности, может проявляться в том, что при изменении одной величины изменяется среднее значение другой величины, такую зависимость называют корреляционной. Примеров такого рода можно привести много. Известно, что такие параметры коллекторов, как открытая пористость и проницаемость связаны с содержанием в породе глинистого материала. Это обуславливает связь между естественным потенциалом скважины и выше названными параметрами. В практике весьма важно уметь изучать такую зависимость, ее характер и тесноту.
Для изучения статистической зависимости разработан специальный аппарат – корреляционный анализ. В частности, для оценки тесноты линейной связи используется коэффициент корреляции. Вычисляется коэффициент корреляции по формуле:
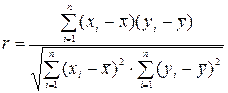, (3.1)
где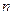 
– число измерений,
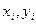- наблюденные значения.
Свойства коэффициента корреляции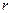 
таковы.
1. |r|≤1, величина безразмерная;
2. Если r=±1, то между случайными величинами существует функциональная линейная зависимость, то есть все точки лежат на прямой линии;
3. Чем дальше величина | r | от единицы и ближе к нулю, тем слабее эта связь:
а) 0,75≤ |r| <1 – связь тесная,
б) 0,50≤ |r| <0,75 - связь средней тесноты,
с) 0,25≤ |r| <0,50 – слабая линейная связь,
д) |r| <0,25 - связи нет;
4. Если значение r положительное, значит зависимость прямая, отрицательное r говорит о наличии обратной связи.
5. При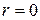 
линейная связь между признакам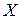и 
и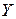 
отсутствует, но может существовать криволинейная корреляционная связь или нелинейная функциональная.
3.3 Пример. Зависимость относительной амплитуды потенциалов СП - aсп и относительной глинистости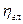 
для пласта АВ1 Нижневартовского района дается значениями, приведенными в табл. 3.1
Таблица 3.1
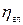
| 0,16 | 0,20 | 0,33 | 0,40 | 0,50 | 0,6 | 0,7 | 0,18 | 0,24 | 0,51 | 0,59 | 0,73 | 0,17 |
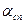
| 0,86 | 0,77 | 0,60 | 0,52 | 0,40 | 0,28 | 0,18 | 0,8 | 0,73 | 0,40 | 0,30 | 0,14 | 0,81 |
Из характера расположения точек можно предположить, что зависимость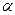 
сп=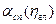 
линейная. Для проверки этой гипотезы найдем оценку значения коэффициента корреляции по формуле (3.1): r=-0,998. Полученное значение подтверждает правильность априорно выдвинутой гипотезы. На рис. 3.1 для наглядности, кроме наблюденных значений, приведена эмпирическая зависимость 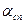от 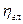в виде прямой линии 
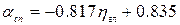, полученная методом наименьших квадратов (см. зад. 4).
3.4 Порядок выполнения задания
1. Вслед за условием задачи и данными в виде таблицы должен идти рисунок, на котором нанесены наблюденные значения.
2. На основе характера расположения точек на рисунке необходимо сформулировать гипотезу о виде эмпирической зависимости между изучаемыми параметрами.
3. Затем следует найти оценку коэффициента корреляции и сделать вывод о виде зависимости.
 |
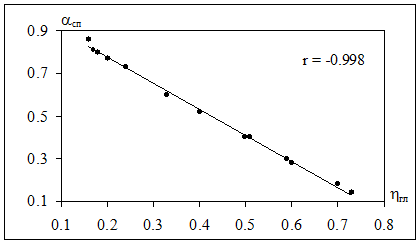Рис. 3.1 Эмпирическая линейная зависимость
3.4 Варианты заданий
1. Зависимость глубины залегания (км) кровли келловейских (Н2) и подошвы меловых (Н1) отложений Южного Мангышлака
| Н1 | 1,69 | 1,51 | 1,52 | 1,42 | 1,33 | 1,04 | 0,93 | 1,31 | 1,10 | 1,61 |
| Н2 | 2,10 | 1,87 | 1,91 | 1,80 | 1,70 | 1,28 | 1,06 | 1,60 | 1,30 | 1,99 |
2. Зависимость суммарной эффективной толщины Нэф (км) от общей толщины Н (км) юрского продуктивного комплекса Арало-Каспийского региона
| Н | 0,12 | 0,32 | 0,50 | 0,58 | 0,64 | 0,99 | 1,02 | 1,10 | 1,10 | 1,32 |
| Нэф | 0,05 | 0,13 | 0,16 | 0,20 | 0,20 | 0,29 | 0,32 | 0,33 | 0,34 | 0,38 |
3. Зависимость параметра насыщения Рн от удельного электрического сопротивления rп (Ом×м) нефтеносного пласта БС1 Усть-Балыкского месторождения
| rп | |||||||||||
| Рн |
4-6. Зависимость коэффициента пористости Кп (д.ед.) от коэффициента проницаемости Кпр (10-3×мкм2) ачимовских отложений одного из месторождений Западной Сибири
4.
| Кп | 0,118 | 0,129 | 0,125 | 0,136 | 0,137 | 0,134 | 0,127 | 0,121 | 0,116 | 0,125 |
| Кпр | 0,156 | 0,198 | 0,184 | 0,231 | 0,239 | 0,221 | 0,191 | 0,166 | 0,148 | 0,182 |
5.
| Кп | 0,133 | 0,131 | 0,127 | 0,12 | 0,126 | 0,119 | 0,12 | 0,125 | 0,14 | 0,119 |
| Кпр | 0,216 | 0,207 | 0,192 | 0,163 | 0,189 | 0,159 | 0,165 | 0,184 | 0,252 | 0,161 |
6.
| Кп | 0,113 | 0,127 | 0,128 | 0,135 | 0,121 | 0,120 | 0,129 | 0,126 | 0,120 | 0,127 |
| Кпр | 0,138 | 0,193 | 0,197 | 0,225 | 0,168 | 0,163 | 0,202 | 0,189 | 0,165 | 0,190 |
7. Зависимость пористости m (%) по керну от коэффициента остаточного водонасыщения Кво (%) пласта БС1 Западно-Сургутского месторождения (средние по скважинам)
| Кво | 0,14 | 0,26 | 0,35 | 0,48 | 0,59 | 0,72 | 0,89 | 0,79 | 0,85 | 0,91 |
| m | 0,25 | 0,24 | 0,23 | 0,22 | 0,21 | 0,19 | 0,19 | 0,19 | 0,18 | 0,18 |
8. Зависимость открытой пористости чистых песчаников mnr от глубины Н (км) для продуктивных пластов Нижневартовского свода
| Н | 1,0 | 1,1 | 1,2 | 1,6 | 1,9 | 2,0 | 2,1 | 2,3 | 2,4 | 2,5 | 1,8 | 1,3 |
| mпч | 0,38 | 0,37 | 0,36 | 0,30 | 0,27 | 0,26 | 0,26 | 0,22 | 0,22 | 0,20 | 0,28 | 0,33 |
9. Зависимость пластового давления Рпл (МПа) от гидростатического давления Рг для продуктивных пластов месторождений нефти и газа Западной Сибири
| Рг | 6,13 | 32,25 | 7,30 | 30,11 | 12,23 | 9,74 | 9,21 | 25,55 | 18,83 |
| Рпл | 6,00 | 32,51 | 7,33 | 29,93 | 12,40 | 9,74 | 9,12 | 25,64 | 18,93 |
10. Зависимость коэффициента проницаемости Кпр (10-3×мкм2) от содержания сильно измененных полевых шпатов Си.п.ш. (%) в породах Западно-Сибирских месторождений
| Си.п.ш. | |||||||||||
| Кпр |
11-13. Зависимость среднесуточного дебита скважины qi (т/сут) в текущем i-том году от дебита qi-1 скважины в предыдущем (i-1)-м году. Ниже приведены среднесуточные дебиты трех скважин по годам
| Год | |||||||||||||
| q | 90,0 | 82,0 | 68,7 | 56,3 | 48,8 | 38,5 | 32,4 | 25,0 | 19,0 | 13,0 | |||
| q | 85,0 | 70,7 | 65,5 | 56,4 | 45,4 | 38,2 | 32,2 | 28,4 | 23,6 |
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2021-02-06 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд