Понятие производной – фундаментальное понятие математического анализа, с помощью которого исследуются процессы и явления в природных, социальных и экономических науках. Изучение разных процессов (механическое движение, химические реакции, расширение жидкости при нагревании и др.) приводят к необходимости вычисления скорости изменения различных величин, т.е., к понятию производной.
Задача 1
Мгновенная скорость прямолинейного движения материальной точки.
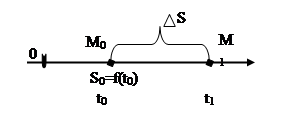
Материальная точка М двигается прямолинейно по закону S=f(t) и в момент времени Пусть за произвольно выбранный промежуток Тогда
За промежуток
Чтобы наиболее точно найти надо Мгновенной скоростью точки, двигающейся прямолинейно, в момент времени
где
Т.е.
| Задача 2
Касательная к кривой.
Касательной АТ к графику функции y=f(x) в точке А называется предельное положение секущей АМ, когда точка М, двигаясь по кривой графика y=f(x), приближается к точке А. Поставим задачу: провести секущую к графику функции y=f(x) в точке А( Касательная – это прямая с общим уравнением y=kx+b, где k=tg Пусть в точке А(
 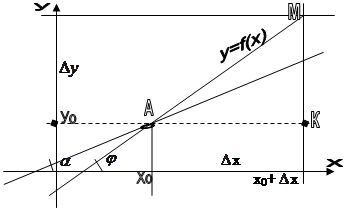
Для этого: 1. аргументу 2. Найдем отношение
3. Если Предельным положением секущей МА является касательная АТ, а угла -угол наклона касательной АТК положительному направления оси ОХ. Тогда
|
Решая обе задачи, поступали по одному и тому же плану:
1) независимой переменной х задавали приращение 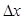 и находили соответствующее приращение
и находили соответствующее приращение 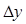 =
= 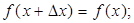
2) находили отношение 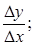
3) находили 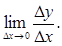
Т.к. такой план приходилось реализовывать неоднократно, и часто его реализация сложна и громоздка, то было введено новое понятие:
Производной функции y=f(x) в точке 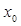 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
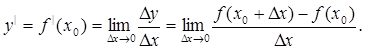
«ТАБЛИЦА ПРОИЗВОДНЫХ»
1. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ:
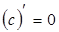
| 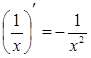
| 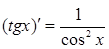
|
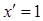
| 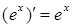
| 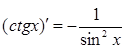
|
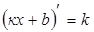
| 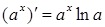
| 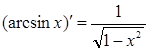
|
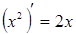
| 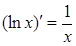 
| 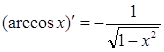
|
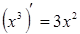
| 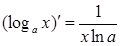
| 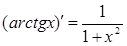
|
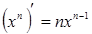
| 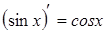
| 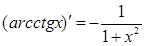
|
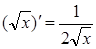
| 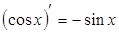
|
2. ТЕОРЕМЫО ПРОИЗВОДНЫХ:
1. Производная суммы-разности двух функций:
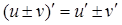
2. Производная произведения двух функций:
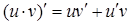
3. Вынесение числового множителя за знак производной:
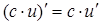 , где с -число.
, где с -число.
4. Производная частного двух функций:
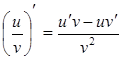 .
.
3. СЛОЖНАЯ ФУНКЦИЯ y = f (g (x)), где y=f (u), u=g (x):
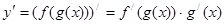
4. ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ 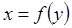 :
:
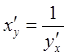 .
.
5. ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ НЕЯВНО F (x; y)=0:
Для нахождения производной по х функции у дифференцируем обе части равенства F (x; y(х))=0, учитывая, что у зависит от х, т.е., рассматриваем ее как сложную функцию, а затем получившееся равенство разрешаем относительно 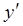 .
.
6. ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ:

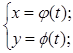
 , где t – параметр, находится по формуле
, где t – параметр, находится по формуле 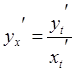 .
.
7. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ:
Так как производная функции с одной переменной также является функцией с одной переменной, то от нее также можно находить производную, которую называют производной второго порядка: 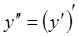 . Аналогично определяют производные более высоких порядков.
. Аналогично определяют производные более высоких порядков.
ПРИМЕРЫ. Нахождение производных различных функций.
Пользуясь таблицей производных и теоремами о производных, вычислить производные следующих функций:
Пример 1: Пользуемся теоремами о производной суммы и о вынесении постоянного множителя за знак производной, а затем таблицей производных элементарных функций.
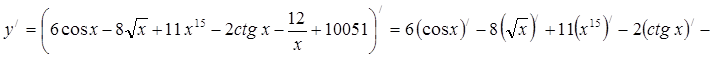
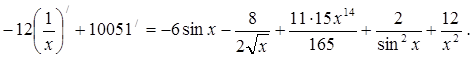
Пример 2: Пользуемся теоремой о производной произведения, а затем таблицей производных элементарных функций.
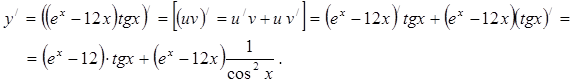
Пример 3. Пользуемся теоремой о производной частного, а затем таблицей производных элементарных функций.
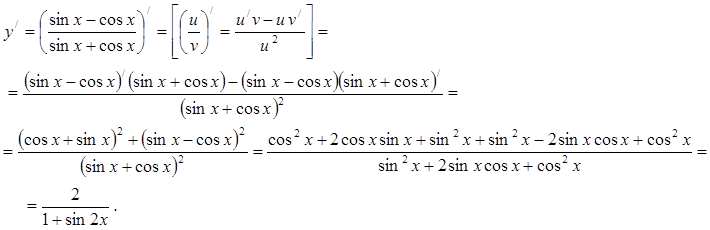
Пример 4. Сложная функция и ее производная:
Каждая сложная функция представляет собой комбинацию двух, трех и более элементарных функций. Если использованы две функции, то одна из них, y=f (u), называется внешней, а другая, u=g (x), - внутренней функцией. Тогда из формулы производной сложной функции 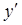 =(f (g (x)))`=f `(g (x)) g`(x) следует, что производную внешней функции надо умножить на производную внутренней функции, причем, при нахождении производной внешней функции используем таблицу производных элементарных функций, учитывая, что вместо аргумента х она содержит функцию.
=(f (g (x)))`=f `(g (x)) g`(x) следует, что производную внешней функции надо умножить на производную внутренней функции, причем, при нахождении производной внешней функции используем таблицу производных элементарных функций, учитывая, что вместо аргумента х она содержит функцию.
1. 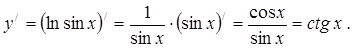
2. 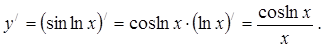
3. 
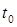 заняла положение
заняла положение 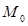 и прошла путь
и прошла путь 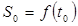 . Найдем скорость точки в момент времени
. Найдем скорость точки в момент времени 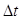 , начиная с
, начиная с 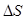 и заняла положение
и заняла положение 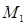 .
.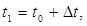
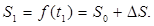
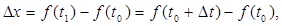 a
a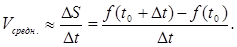
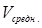 ,
,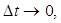 тогда
тогда 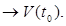
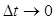 .
. 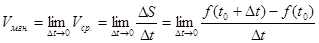
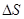 - приращение пути.
- приращение пути.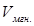 прямолинейно двигающейся точки есть предел отношения приращения пути
прямолинейно двигающейся точки есть предел отношения приращения пути 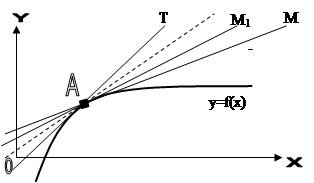
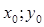 ).
).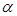 , где
, где 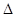 y
y
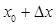 , и найдем соответствующее значение функции
, и найдем соответствующее значение функции 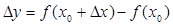 .
.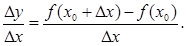 Из
Из 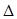 АМК имеем:
АМК имеем: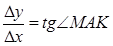 , но
, но 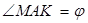 - углу наклона секущей АМ к положительному направлению оси ОХ, значит
- углу наклона секущей АМ к положительному направлению оси ОХ, значит 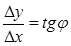 .
.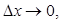 то
то 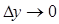 и М
и М 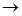 А (двигаясь по кривой
А (двигаясь по кривой 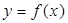 ).
).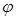 -угол
-угол 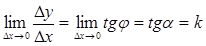 - угловой коэффициент касательной.
- угловой коэффициент касательной.