Лекция 8
Критерий Гурвица.

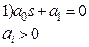
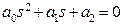


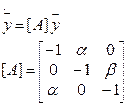

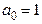
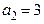
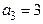
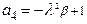
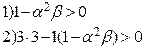


Недостатки алгебраических критериев:
1. Большой объем вычислительных работ.
2. Сложность выражений при установлении влияния параметров САР на устойчивость (особенно при высоких порядках).
Частотные критерии устойчивости (ЧКУ)
В большинстве случаев ЧКУ используется в качестве графоаналитических критериев, что обеспечивает наглядность инженерных расчетов.
В основе ЧКУ лежит принцип аргумента:

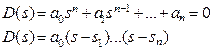
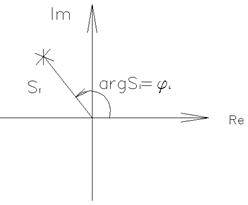
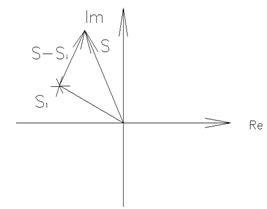
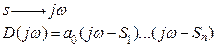 (1)
(1)
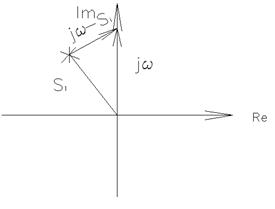
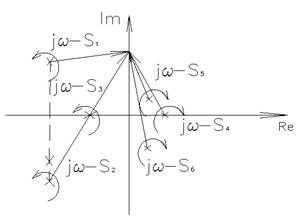
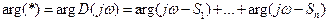
Вектора будут поворачиваться (приω от -∞ до +∞):
1) Те, что слева (устойчивые) – на угол π против часовой стрелки (на +π)
2) Правые – наπ по часовой (на –π)
Пусть мы имеем k неустойчивость корней и n-k устойчивость.
Определение принципа аргумента
Разность n-k корней уравнения D(S)=0? Находящихся в левой полуплоскости и k корней в правой полуплоскости, умноженная на π, отражает собой изменение аргумента вектора D(jω) при возрастании частоты от -∞ до +∞.

Для устойчивости системы должны потребовать k=0!
Тогда 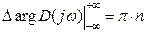
Частотный критерий устойчивости Михайлова
(основан на рассмотрении поведения годографа, определяемого характеристическим уравнением замкнутой системы).
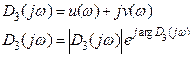
 содержит ω в четной степени (v–в нечетной)
содержит ω в четной степени (v–в нечетной)
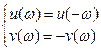
Вследствие этого, можно рассмотреть изменение ω только от 0 до ∞. Так как вторая ветвь является зеркальным отражением относительно оси абсцисс

Годограф D3(jω) – (характеристическая) кривая Михайлова. Для устойчивости замкнутой системы необходимо и достаточно, чтобы вектор D3(jω), описываемый своим концом кривую Михайлова, при изменении частоты от 0 до ∞, начав свое движение с положительной действительной оси и вращаясь против часовой стрелки последовательно проходил nквадрантов, нигде не обращался в ноль.

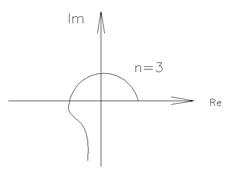
Доп.
Угол φ должен быть монотонно возрастающим
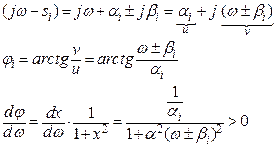
Значит φ-монотонно возрастающая функция

Примеры.
1) 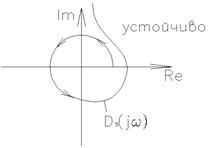 π против часовой стрелки
π против часовой стрелки
2) φ возрастает
3) Δ=5π/2
4) Не обращается в ноль
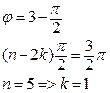


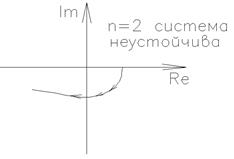
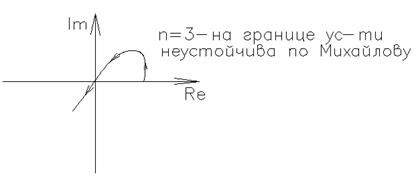
Второй вариант анализа устойчивости системы с использованием
Системы ЧКУ Михайлова
D3(jω)=u(ω)+j∙v(ω)
Можно судить об устойчивости по расположению корней  .
.
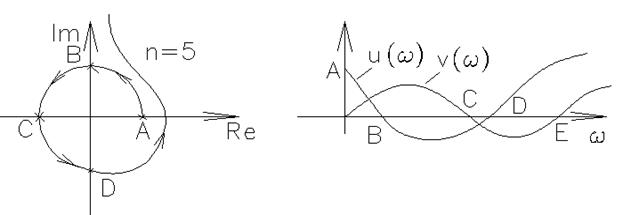
Для устойчивости системы вектор D3(jω) в соответствии с критерием Михайлова последовательно проходит n квадрантов. При этом поочередно будут обращаться в ноль то вещественная (U(ω), то мнимая (v(ω)) части D3(jω)). Следовательно, корни уравнений u(ω)=0 и v(ω)=0 должны обладать свойством перемежаемости.

Пример.
S5+S4+7S3+4S2+10S+3=0
Не изображая годограф, по критерию Михайлова сделать вывод об устойчивости.

| u | √3 | ||||
| v | √2 | √5 |
=>система устойчива

| u | √0,01 | √14 | ||||
| v | 1/√3 | √3 |
Критерий Найквиста для статических и астатических систем
Позволяет установить по АФХ разомкнутых систем необходимое и достаточное условие устойчивости замкнутых систем.
Его еще называют амплитудно-фазовым критерием устойчивости.
Имеем разомкнутую систему


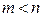
Замкнем систему:
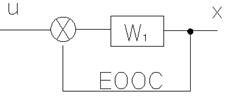
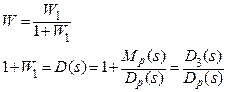
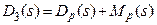 - характеристический полином для замкнутой системы
- характеристический полином для замкнутой системы
 . Нас всегда интересуют полюсы (корни знаменателя).
. Нас всегда интересуют полюсы (корни знаменателя).
У них один порядок (n)
Обозначим корни характеристических уравнений для:
· Замкнутой системы àS’i
· Разомкнутой à Si

K – разом.
K’– замкн.
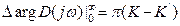
Найквист предложил:
Рассмотрим D(jω) в виде
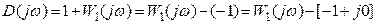
Рассмотрим 2 варианта:
1. Разомкнутая система устойчива. K=0 (все корни слева).
Чтобы замкнутая система была устойчива, необходимо, чтобы приращение аргумента вектора D=-πk’=0=>k’=0
Если разомкнутая система устойчива, то для устойчивости замкн. необходимо, чтобы АФК разомкнутой системы не охватывало критическую точку (-1;0)

Приращение φ=0
2). Разомкнутая система неудобства. Тогда для устойчивости в замкнутом состояни и необходимо и достаточно, чтобы все корни замкнутой системы были слева => 
Неустойчивая разомкнутая система с k корнями в правой полуплоскости, будет устойчива в замкнутом состоянии, если АФК разомкнутой системы при возрастании ω от 0 до ∞. Охватит критическую точку против часовой стрелки 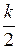 раз.
раз.
1) K=2

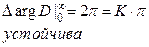
2) K=1

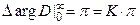
Устойчива (в замкнутом состоянии).
3) K=1
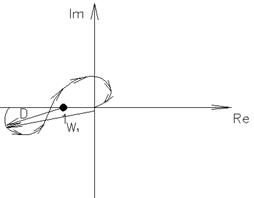
Приращение по часовой стрелке => -π
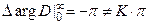
Неустойчива.
4) K=2
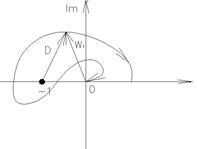
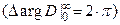
Астатические системы

 - степень астатизма
- степень астатизма
 ω=0 W1(∞)à∞
ω=0 W1(∞)à∞
Разрывная функция (при переходе через 0)
Появляется неопределенность при устойчивом приращении аргумента вектора D.
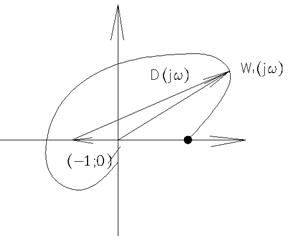
В этом случае АФЧХ вектора W1(jω) уходит в ∞ при подходе к нулевой частоте (с обеих сторон).
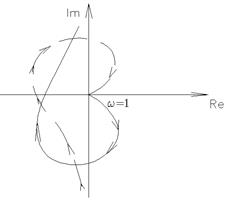
Это делает невозможным непосредственное применение критерия Найквиста.
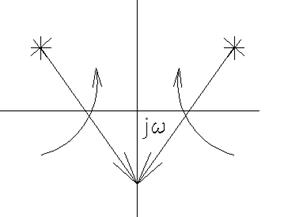
Как поворачивается сам jω-?
Прием:
Полюс обходят справа по окружности бесконечно малого радиуса.
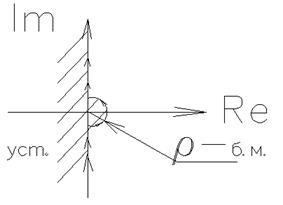
Тогда вместо S=0 à 
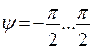
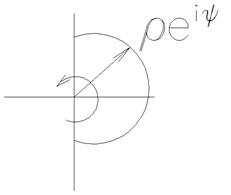
Подставим в знаменатель:

Тогда
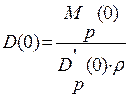
Видно, что обход полюса в начале координат против часовой стрелки соответствует переходу годографа по часовой стрелке.

Формулировка критерия Найквиста – та же, что и для статических систем. Но необходимо дополнить АФХ системы окружностью бесконечно большого радиуса с тем, чтобы 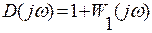 при ω от -∞ до +∞ перемещалось по часовой стрелке.
при ω от -∞ до +∞ перемещалось по часовой стрелке.
Если ω – от 0 до ∞, то ∆φ=  для
для 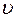 =1
=1
=  для
для  =2
=2
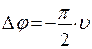
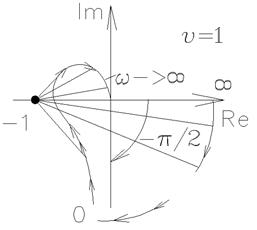
Разомкнутая –устойчива =>замкнутая-устойчивая.
Остальные – как для статической.
