ГЛАВА IV
МЕТОДЫКОРРЕЛЯЦИОННОГО
И РЕГРЕССИОННОГО АНАЛИЗОВ
1. Выборочный коэффициент корреляции. Методы корреляционного и регрессионного анализов широко применяются для выявления и описания зависимостей между случайными величинами по экспериментальным данным. Для экспериментального изучения зависимости между случайными величинами X и Y производят некоторое количество n независимых опытов. Результат i -го опыта дает пару значений 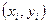 , i = 1, 2, …, п.
, i = 1, 2, …, п.
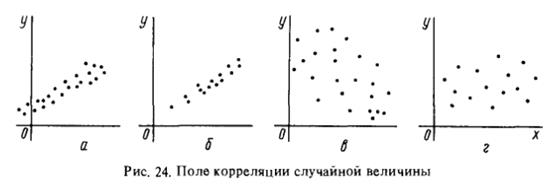
О наличии или отсутствии корреляции между двумя случайными величинами качественно можно судить по виду поля корреляции, нанеся точки 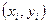 на координатную плоскость. Положительная корреляция между случайными величинами представлена на рис. 24, а. Еще более ярко выраженная корреляция, близкая к линейной функциональной, показана на рис. 24, б. На рис. 24, в приведен пример сравнительно слабой отрицательной корреляции, а на рис. 24, г — пример фактически некоррелированных случайных величин.
на координатную плоскость. Положительная корреляция между случайными величинами представлена на рис. 24, а. Еще более ярко выраженная корреляция, близкая к линейной функциональной, показана на рис. 24, б. На рис. 24, в приведен пример сравнительно слабой отрицательной корреляции, а на рис. 24, г — пример фактически некоррелированных случайных величин.
Для количественной оценки тесноты связи служит выборочный коэффициент корреляции.
Как было показано (см. гл. II), состоятельными и несмещенными оценками для математических ожиданий 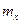 и
и  служат выборочные средние:
служат выборочные средние:


Состоятельными и несмещенными оценками дисперсий  и
и  служат выборочные дисперсии:
служат выборочные дисперсии:


Наконец, состоятельной и несмещенной оценкой ковариации 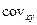 служит выборочная ковариация:
служит выборочная ковариация:

По этим оценкам получают выборочный коэффициент корреляции:
 (IV.1)
(IV.1)
Выборочный коэффициент корреляции  дает состоятельную, но смещенную оценку для коэффициента корреляции генеральной совокупности, эта оценка имеет смещение, равное
дает состоятельную, но смещенную оценку для коэффициента корреляции генеральной совокупности, эта оценка имеет смещение, равное  . Величина смещения убывает обратно пропорционально числу опытов n и при
. Величина смещения убывает обратно пропорционально числу опытов n и при  составляет менее 1%.
составляет менее 1%.
Выборочный коэффициент корреляции 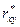 , так же как и
, так же как и  — коэффициент корреляции генеральной совокупности, по абсолютной величине не превосходит единицы:
— коэффициент корреляции генеральной совокупности, по абсолютной величине не превосходит единицы:

Выборочный коэффициент корреляции не изменяется при изменении начала отсчета и масштаба величин X и Y (см. свойства коэффициента корреляции генеральной совокупности, с. 25). Это свойство позволяет существенно упростить вычисления.
Коэффициент корреляции одинаково отмечает долю случайности и криволинейность связи между X и Y. Зависимость между X и Y может быть близкой к функциональной, но существенно нелинейной, а коэффициент корреляции будет значительно меньше единицы.
При достаточно большом объеме выборки n выборочный коэффициент корреляции  приближенно равен генеральному коэффициенту
приближенно равен генеральному коэффициенту 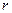 . Однако оценить возникающую при этом погрешность затруднительно. Для этого нужно знать распределение
. Однако оценить возникающую при этом погрешность затруднительно. Для этого нужно знать распределение  как случайной величины. Это распределение зависит от генерального коэффициента корреляции
как случайной величины. Это распределение зависит от генерального коэффициента корреляции 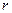 , который неизвестен. Для проверки гипотезы об отсутствии корреляции необходимо проверять, значимо ли отличается
, который неизвестен. Для проверки гипотезы об отсутствии корреляции необходимо проверять, значимо ли отличается  от нуля. Для проверки нулевой гипотезы H°:
от нуля. Для проверки нулевой гипотезы H°: 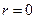 можно использовать нормальное распределение со стандартом:
можно использовать нормальное распределение со стандартом:
 (IV.2)
(IV.2)
Если в качестве доверительной вероятности взять  , коэффициент корреляции находится в следующих доверительных границах:
, коэффициент корреляции находится в следующих доверительных границах:
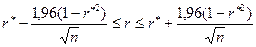 (IV.3)
(IV.3)
С вероятностью 0,95 можно утверждать, что зависимость между случайными величинами существует, если 0 не содержится внутри доверительного интервала, т. е. если
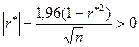 (IV.4)
(IV.4)
При малом числе экспериментов и сравнительно высокой корреляции распределение коэффициента корреляции существенно отличается от нормального (рис. 25, a).Для построения доверительного интервала можно воспользоваться преобразованием Фишера:
 (IV.5)
(IV.5)
отсюда
 (IV.6)
(IV.6)
Распределение z является почти неизменным по форме при меняющихся  и n и c возрастанием n быстро приближается к нормальному (рис. 25, б)со средним, равным
и n и c возрастанием n быстро приближается к нормальному (рис. 25, б)со средним, равным
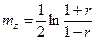 (IV.7)
(IV.7)
и со стандартом
 (IV.8)
(IV.8)
Тогда с доверительной вероятностью 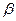 значение неизвестного
значение неизвестного  находится в пределах
находится в пределах
 (IV.9)
(IV.9)
где 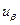 — квантиль нормального распределения. При доверительной вероятности
— квантиль нормального распределения. При доверительной вероятности  ,
, 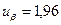 , отсюда
, отсюда
 (IV.10)
(IV.10)
После нахождения доверительных границ для 
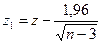 (IV.11)
(IV.11)
и
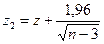
можно найти доверительные границы для генерального коэффициента корреляции, подставляя  и
и  в формулу (IV.5).
в формулу (IV.5).

2. Коэффициенты частной корреляции. При исследовании зависимости величины у от двух факторов 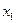 и
и  наличие корреляции между у и
наличие корреляции между у и  и корреляции между
и корреляции между 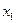 и
и  будет влиять на корреляцию между у и
будет влиять на корреляцию между у и 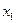 . Для того чтобы устранить влияние
. Для того чтобы устранить влияние  ,необходимо измерить корреляцию между у и
,необходимо измерить корреляцию между у и 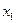 , когда
, когда  постоянно. Для этой цели в статистике применяют частные коэффициенты корреляции:
постоянно. Для этой цели в статистике применяют частные коэффициенты корреляции:
 (IV.12)
(IV.12)
 (IV.13)
(IV.13)
Частный коэффициент корреляции 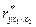 оценивает степень влияния фактора
оценивает степень влияния фактора 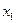 на у при условии, что влияние
на у при условии, что влияние  на у исключено. В обозначении частного коэффициента корреляции этот исключенный фактор поставлен в индексе после точки. При изучении зависимости у от трех факторов
на у исключено. В обозначении частного коэффициента корреляции этот исключенный фактор поставлен в индексе после точки. При изучении зависимости у от трех факторов 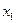 ,
,  и
и  частный коэффициент корреляции между у и
частный коэффициент корреляции между у и 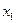 при условии, что
при условии, что  и
и  будут постоянными, можно вычислить по формуле
будут постоянными, можно вычислить по формуле
 (IV.14)
(IV.14)
При переходе от парных коэффициентов корреляции к частным может существенно измениться не только величина коэффициента корреляции, но и знак. Проиллюстрируем это на примере.
Исследовалась скорость коррозии (K)образцов стали, содержащих серу (S), фосфор (Р) и медь (Cu) в растворе лимонной кислоты.
На основании выборки из 39 опытов были получены значения коэффициентов парной корреляции:

По формуле (IV.12) найдем частные коэффициенты корреляции, исключив влияние одного из факторов:

Сопоставление величин парных и частных коэффициентов корреляции показывает, что влияние, например, фосфора на скорость коррозии при постоянном содержании меди больше, чем при переменном, а влияние фосфора на скорость коррозии при постоянном содержании серы меньше, чем при переменном:

Частные коэффициенты корреляции, вычисленные по формуле (IV.14) в предположении, что устранено влияние двух факторов, приведены ниже:
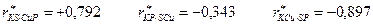
Коэффициент парной корреляции между скоростью коррозии и содержанием фосфора при меняющихся концентрациях меди и серы положительный  ; частный коэффициент корреляции
; частный коэффициент корреляции  .
.
Таким образом, анализ корреляции дал возможность установить характер и степень влияния количества серы, фосфора и меди, содержащихся в стали, на скорость ее коррозии в растворе лимонной кислоты.
В общем случае для расчета коэффициентов частной корреляции можно воспользоваться выборочной корреляционной матрицей:

Коэффициент частной корреляции между 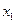 и у определится по формуле
и у определится по формуле
 (IV.15)
(IV.15)
где  — минор, получаемый вычеркиванием i -й строки и столбца y;
— минор, получаемый вычеркиванием i -й строки и столбца y; 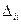 и
и  — минор, получаемый вычеркиванием i -й (j -й) строки и i -го (j -го) столбца. Например, для корреляционной матрицы
— минор, получаемый вычеркиванием i -й (j -й) строки и i -го (j -го) столбца. Например, для корреляционной матрицы
 (IV.16)
(IV.16)
коэффициент частной корреляции  между
между 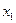 и у определится следующим образом:
и у определится следующим образом:
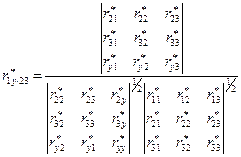 (IV.17)
(IV.17)
При интерпретации результатов корреляционного анализа нужно иметь в виду, что коэффициент корреляции — чисто статистический показатель. Он не содержит предположения, что изучаемые величины находятся в причинно-следственной связи. Поэтому любая трактовка корреляционной зависимости должна основываться на информации физико-химического характера.
3. Приближенная регрессия. Метод наименьших квадратов. Для характеристики формы связи при изучении корреляционной зависимостипользуются уравнением приближенной регрессии. Задача ставится такимобразом: по данной выборке объема n найти уравнение приближеннойрегрессии и оценить допускаемую при этом ошибку. Эта задача решаетсяметодами регрессионного и корреляционного анализа. Уравнение приближенной регрессии существенно зависит от выбираемого метода приближения. В качестве такого метода обычно выбирают метод наименьшихквадратов. Пусть задан некоторый класс функций f (x),накладывающихна выборку одинаковое число связей l. Число связей l равно числунеопределенных коэффициентов, входящих в аналитическое выражениеэтой функции. Чаще всего используют многочлены различной степени.Наилучшее уравнение приближенной регрессии дает та функция израссматриваемого класса, для которой сумма квадратов имеет наименьшее значение
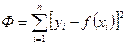 (IV.18)
(IV.18)
При нормальном распределении случайных величин метод наименьших квадратов обосновывается в теории вероятностей как частный случай принципа максимума правдоподобия.
Предположим, что уравнение истинной регрессии выражается формулой 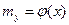 , а экспериментальные точки отклоняются от этой зависимости вследствие случайных ошибок измерения. Допустим, что ошибки измерения подчиняются нормальному закону распределения. Тогда результат i -го опыта есть случайная величина
, а экспериментальные точки отклоняются от этой зависимости вследствие случайных ошибок измерения. Допустим, что ошибки измерения подчиняются нормальному закону распределения. Тогда результат i -го опыта есть случайная величина 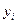 , распределенная по нормальному закону с математическим ожиданием
, распределенная по нормальному закону с математическим ожиданием  и средним квадратичным отклонением
и средним квадратичным отклонением  , характеризующим ошибку воспроизводимости.
, характеризующим ошибку воспроизводимости.
Полагая, что все эксперименты равноточны, имеем:

Тогда нормальный закон, по которому распределена величина 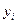 ,можно записать в виде
,можно записать в виде
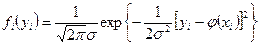
В результате опыта — ряда измерений — произошло следующее событие: случайные величины  ,
, 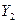 , …,
, …,  приняли совокупность значений
приняли совокупность значений 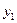 ,
,  , …,
, …,  . В соответствии с принципом максимального правдоподобия (см. гл. II, с. 30) подберем так математические ожидания
. В соответствии с принципом максимального правдоподобия (см. гл. II, с. 30) подберем так математические ожидания  ,
,  , …,
, …,  , чтобы вероятность этого события Р была максимальна.
, чтобы вероятность этого события Р была максимальна.
Вероятность  того, что случайная величина
того, что случайная величина 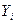 попадет в интервал
попадет в интервал  ,
,  в первом приближении, равна:
в первом приближении, равна:

Найдем вероятность того, что система независимых случайных величин 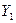 ,
, 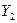 , …,
, …,  примет совокупность значений из интервалов
примет совокупность значений из интервалов  ,
,  ,
,  :
:
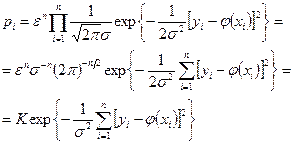
где K — коэффициент, не зависящий от  .
.
Очевидно, что при заданном  максимум вероятности Р получится в случае, когда стоящая в показателе степени экспоненты сумма минимальна, т.е.
максимум вероятности Р получится в случае, когда стоящая в показателе степени экспоненты сумма минимальна, т.е.
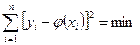
По методу наименьших квадратов можно обрабатывать любые экспериментальные данные, однако оптимальность этой процедуры доказывается только для нормального распределения. При этом можно говорить о достаточных статистиках, т. е. таких функциях от результатов наблюдений (оценках для параметров генеральной совокупности), при помощи которых извлекается вся информация об этих параметрах, содержащаяся в эксперименте.
Задача определения коэффициентов уравнения регрессии по методу наименьших квадратов сводится практически к определению минимума функции многих переменных. Если
 (IV.19)
(IV.19)
есть функция дифференцируемая и требуется выбрать  ,
,  ,
,  так, чтобы
так, чтобы
 (IV.20)
(IV.20)
необходимым условием минимума  является выполнение равенств
является выполнение равенств
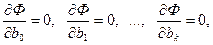 (IV.21)
(IV.21)
или
 (IV.22)
(IV.22)
После преобразования
 (IV.23)
(IV.23)
Система уравнений (IV.23) содержит столько же уравнений, сколько неизвестных коэффициентов  ,
,  ,
,  , …,
, …, 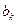 входит в уравнение регрессии, и называется в математической статистике системой нормальных уравнений.
входит в уравнение регрессии, и называется в математической статистике системой нормальных уравнений.
Функция 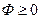 при любых
при любых  ,
, 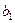 ,
,  , …,
, …, 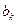 , следовательно, у нее обязательно должен существовать хотя бы один минимум. Поэтому если система нормальных уравнений имеет единственное решение, то оно и является минимумом для функции Ф.
, следовательно, у нее обязательно должен существовать хотя бы один минимум. Поэтому если система нормальных уравнений имеет единственное решение, то оно и является минимумом для функции Ф.
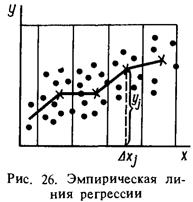
При изучении зависимости от одного переменного параметра полезно для определения вида уравнения регрессии построить эмпирическую линию регрессии. Для этого весь диапазон изменения x на поле корреляции (рис. 26) разбивается на k равных интервалов 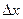 .Все точки, попавшие в данный интервал
.Все точки, попавшие в данный интервал  , относят к его середине
, относят к его середине 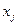 . Для этого подсчитывают частные средние
. Для этого подсчитывают частные средние 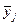 для каждого интервала
для каждого интервала
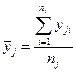 (IV.24)
(IV.24)
где 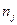 – число точек в интервале
– число точек в интервале  ; при этом
; при этом
 (IV.25)
(IV.25)
n – объем выборки. Затем последовательно соединяют точки 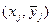 отрезками прямой. Полученная ломаная называется эмпирической линией регрессии y по x. По виду эмпирической линии регрессии можно подобрать уравнение регрессии
отрезками прямой. Полученная ломаная называется эмпирической линией регрессии y по x. По виду эмпирической линии регрессии можно подобрать уравнение регрессии  .
.
 4. Линейная регрессия от одного параметра. Требуется определить по методу наименьших квадратов коэффициенты линейного уравнения регрессии
4. Линейная регрессия от одного параметра. Требуется определить по методу наименьших квадратов коэффициенты линейного уравнения регрессии
 (IV.25)
(IV.25)
по выборке объема n. Система нормальных уравнений при этом имеет вид

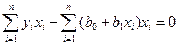
или
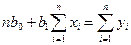
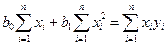 (IV.27)
(IV.27)
Коэффициенты  и
и 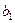 легко найти при помощи определителей:
легко найти при помощи определителей:
 (IV.28)
(IV.28)
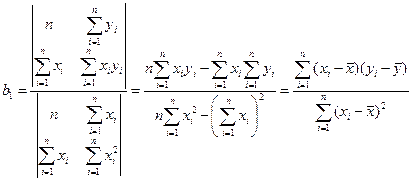 (IV.29)
(IV.29)
 проще найти по известному
проще найти по известному 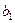 из первого уравнения системы:
из первого уравнения системы:
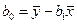 (IV.30)
(IV.30)
Уравнение (IV.30) показывает, что между коэффициентами  и
и 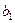 существует корреляционная зависимость. Для оценки силы линейной связи (IV.26) вычисляется коэффициент корреляции
существует корреляционная зависимость. Для оценки силы линейной связи (IV.26) вычисляется коэффициент корреляции  :
:
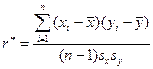 (IV.31)
(IV.31)
где 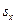 и
и 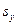 – выборочные среднеквадратические отклонения
– выборочные среднеквадратические отклонения
Из уравнений (IV.29) и (IV.31) имеем
 (IV.32)
(IV.32)
Пример 1. Требуется определить зависимость растворимости хлорида бария в воде (у) и присутствия хлорида кальция (x) при 70°С. Объем выборки  . Экспериментальные данные приведены ниже:
. Экспериментальные данные приведены ниже:
 , %............ 0 5 8 10 15 20
, %............ 0 5 8 10 15 20
у (растворимость BaCl2, %).... 32 25 20 17 11 5
Решение. Определим коэффициенты уравнения линейной регрессии вида

Коэффициент 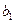 определим по формуле (IV.29),
определим по формуле (IV.29),  - по формуле (IV.30). Для этого экспериментальные данные и результаты расчета представим в виде таблицы.
- по формуле (IV.30). Для этого экспериментальные данные и результаты расчета представим в виде таблицы.
| Номер опыта | x | у | 
| xy | 
| 
| 
|
| ∑ |
Проверку вычислений можно провести по формуле
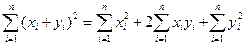 (IV.33)
(IV.33)
В данном примере имеем  , т.е. вычисления проведены правильно.
, т.е. вычисления проведены правильно.
Используем полученные в таблице суммы для определения коэффициентов  и
и 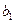 :
:
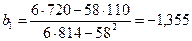 ;
;  .
.
По формуле (IV.32) определим выборочный коэффициент корреляции
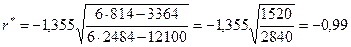
Коэффициент корреляции очень близок к единице, следовательно, зависимость между x и y является практически линейной в изученном диапазоне и имеет вид
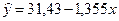
После того как уравнение регрессии найдено, необходимо провести статистический анализ результатов. Этот анализ заключается в проверке всех коэффициентов регрессии в сравнении с ошибкой воспроизводимости и адекватности уравнения. Такое исследование называется регриссионным анализом. Примем при произведении регрессионного анализа следующие допущения:
1. Входной параметр x измеряется с пренебрежимо малой ошибкой по сравнению с ошибкой в определении y. Большая ошибка у объясняется наличием в каждом процессе невыявленных переменных, не вошедших в уравнение регрессии.
2. Результаты наблюдении 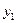 ,
, 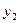 , …,
, …,  над выходной величиной у представляют собой независимые, нормально распределенные случайные величины.
над выходной величиной у представляют собой независимые, нормально распределенные случайные величины.
3. При проведении эксперимента с объемом выборки n при условии, что каждый опыт повторен m раз, i = 1, 2, …, n. выборочные дисперсии 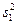 ,
,  , …,
, …, 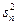 должны быть однородны.
должны быть однородны.
Однородность дисперсий при одинаковом числе степеней свободы проверяют по критерию Кохрена, а при разном – по критерию Бартлете. Определенная по параллельным опятам дисперсия воспроизводимости  необходима для оценки значимости коэффициентов уравнения регрессии и проверки адекватности уравнения эксперименту.
необходима для оценки значимости коэффициентов уравнения регрессии и проверки адекватности уравнения эксперименту.
Оценку значимости коэффициентов производится по критерию Стьюдента
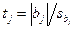 (IV.34)
(IV.34)
где 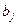 – j -й коэффициент уравнения регрессии;
– j -й коэффициент уравнения регрессии;  – среднее квадратичное отклонение j -го коэффициента.
– среднее квадратичное отклонение j -го коэффициента.
Если 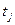 больше табличного
больше табличного  для выбранного уровня значимости р и числа степеней свободы
для выбранного уровня значимости р и числа степеней свободы 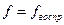 , то коэффициент
, то коэффициент 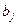 значимо отличается от нуля;
значимо отличается от нуля;  определяется по закону накопления ошибок (II.36)
определяется по закону накопления ошибок (II.36)
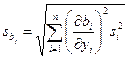 (IV.35)
(IV.35)
Если выборочные дисперсии 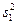 ,
,  , …,
, …, 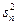 однородны, получим
однородны, получим
 (IV.36)
(IV.36)
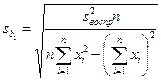 (IV.37)
(IV.37)
Незначимые коэффициенты исключаются из уравнения регрессии. Оставшиеся коэффициенты пересчитываются заново, поскольку коэффициенты закоррелированы друг с другом. Адекватность уравнения проверяется по критерию Фишера:
 (IV.38)
(IV.38)
где 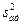 – дисперсия адекватности:
– дисперсия адекватности:  – дисперсия воспроизводимости;
– дисперсия воспроизводимости;
 (IV.39)
(IV.39)
 – сумма квадратов адекватности;
– сумма квадратов адекватности;
 (IV.40)
(IV.40)
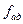 – число степеней свободы дисперсии адекватности;
– число степеней свободы дисперсии адекватности;
 (IV.41)
(IV.41)
l – число коэффициентов в уравнении регрессии;
 – сумма квадратов, связанная с дисперсией воспроизводимости
– сумма квадратов, связанная с дисперсией воспроизводимости  ,
,
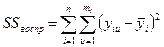 (IV.42)
(IV.42)
 (IV.43)
(IV.43)
 (IV.44)
(IV.44)
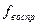 – число степеней свободы дисперсии воспроизводимости;
– число степеней свободы дисперсии воспроизводимости;
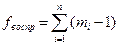 (IV.45)
(IV.45)
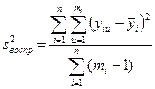 (IV.46)
(IV.46)
 – остаточная сумма квадратов;
– остаточная сумма квадратов;
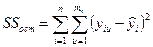 (IV.47)
(IV.47)
 (IV.48)
(IV.48)
 - число степеней свободы остаточной дисперсии
- число степеней свободы остаточной дисперсии  ;
;
 (IV.49)
(IV.49)
Если:
 (IV.50)
(IV.50)
окажется меньше табличного значения  для уровня значимости p и числа степеней свободы
для уровня значимости p и числа степеней свободы 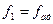 и
и  , уравнение адекватно эксперименту.
, уравнение адекватно эксперименту.
Для одинакового числа опытов  вычисления упрощаются:
вычисления упрощаются:
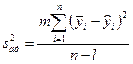 (IV.51)
(IV.51)
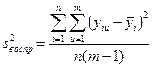 (IV.52)
(IV.52)
Если опыты проведены без параллельных, а для получения дисперсии воспроизводимости проделана серия из m опытов, тогда
 (IV.53)
(IV.53)
 (IV.54)
(IV.54)
 (IV.55)
(IV.55)
При отсутствии параллельных опытов и дисперсий воспроизводимости можно оценить качество аппроксимации принятым уравнением, сравнив  и дисперсию относительно среднего
и дисперсию относительно среднего  :
:
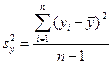 (IV.56)
(IV.56)
по критерию Фишера:
 (IV.57)
(IV.57)
В этом случае критерий Фишера показывает, во сколько раз уменьшается рассеяние относительно полученного уравнения регрессии по сравнению с рассеянием относительно среднего. Чем больше значение F превышает табличное  для выбранного уровня значимости p и чисел степеней свободы
для выбранного уровня значимости p и чисел степеней свободы 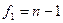 и
и  , тем эффективнее уравнение регрессии.
, тем эффективнее уравнение регрессии.
5. Параболическая регрессия. Если уравнение регрессии представляет собой полином некоторой степени, то при применении метода наименьших квадратов коэффициенты этого полинома находят решением системы линейных уравнений. Например, требуется определить по методу наименьших квадратов коэффициенты квадратичной функции – параболы второго порядка:
 (IV.58)
(IV.58)
При этом
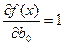


и система нормальных уравнений имеет вид:
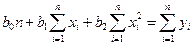
 (IV.59)
(IV.59)
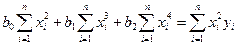
Аналогичными по структуре уравнениями будут определяться коэффициенты любого порядка.
Адекватности уравнения регрессии эксперименту добиваются повышением степени полинома. При этом в связи с наличием корреляции между коэффициентами все коэффициенты регрессии нужно вычислять заново. При переходе от k -й степени полинома к  -й в правой части уравнения регрессии добавляется одно слагаемое вида
-й в правой части уравнения регрессии добавляется одно слагаемое вида  , но все
, но все  коэффициента приходится рассчитывать заново. В качестве критерия при вычислениях рассматривается остаточная дисперсия:
коэффициента приходится рассчитывать заново. В качестве критерия при вычислениях рассматривается остаточная дисперсия:

Как только  перестанет быть значимо меньше
перестанет быть значимо меньше  увеличение степени k нужно прекратить. Значимость различия между
увеличение степени k нужно прекратить. Значимость различия между  и
и  проверяется по критерию Фишера:
проверяется по критерию Фишера:
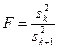
Если полученное F -отношение меньше табличного  для выбранного уровня значимости и чисел степеней свободы
для выбранного уровня значимости и чисел степеней свободы 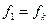 и
и  увеличение степени k нужно прекратить.
увеличение степени k нужно прекратить.
6. Полиномы Чебышева. Уравнение регрессии, выраженное через полиномы Чебышева имеет вид
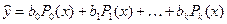 (IV.60)
(IV.60)
где 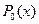 ,
,  , …,
, …,  – ортогональные полиномы Чебышева на множестве точек
– ортогональные полиномы Чебышева на множестве точек 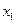 ,
,  , …,
, …,  . Это означает, что для всех
. Это означает, что для всех  выполняются соотношения
выполняются соотношения
 (IV.61)
(IV.61)
где  зависит только от объема выборки n. Зная многочлены Чебышева
зависит только от объема выборки n. Зная многочлены Чебышева 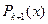 , при каждом увеличении степени уравнения регрессии необходимо вычислять только коэффициент
, при каждом увеличении степени уравнения регрессии необходимо вычислять только коэффициент 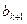 . Многочлены Чебышева определяются по формулам
. Многочлены Чебышева определяются по формулам
 (IV.62)
(IV.62)
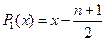 (IV.63)
(IV.63)
…………………………
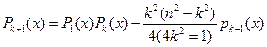 (IV.64)
(IV.64)
Например,
 (IV.65)
(IV.65)
 (IV.66)
(IV.66)
 (IV.67)
(IV.67)
Определяя коэффициенты  ,
, 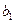 , …,
, …, 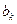 уравнения регрессии (IV.60) по методу наименьших квадратов, получим
уравнения регрессии (IV.60) по методу наименьших квадратов, получим

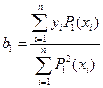
……………………. (IV.68)
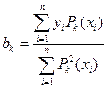
Вычисленные по формулам (IV.68) коэффициенты 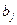 не зависят от того, каков будет порядок определяемого уравнения регрессии. При нахождении уравнения регрессии методом последовательных уточнений используются все ранее найденные
не зависят от того, каков будет порядок определяемого уравнения регрессии. При нахождении уравнения регрессии методом последовательных уточнений используются все ранее найденные  . Повышение порядка уравнения регрессии на 1 приводит к определению только одного коэффициента. При этом удобными получаются формулы для расчета остаточной дисперсии для уравнения регрессии k -го порядка:
. Повышение порядка уравнения регрессии на 1 приводит к определению только одного коэффициента. При этом удобными получаются формулы для расчета остаточной дисперсии для уравнения регрессии k -го порядка:
 (IV.69)
(IV.69)
где суммы квадратов отклонений  определяются по рекуррентной формуле
определяются по рекуррентной формуле
 (IV.70)
(IV.70)
Необходимо только заранее подсчитать  :
:
 (IV.71)
(IV.71)
При равноотстоящих значений аргумента
 ;
;  ; ………;
; ………;  ,
,
где h – шаг интерполяции, вычисления коэффициентов облегчаются. Сделаем замену переменных:
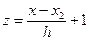 (IV.72)
(IV.72)
Тогда каждое значение 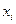 заменяется своим номером, т.е.
заменяется своим номером, т.е.  . Определим коэффициенты уравнения регрессии вида
. Определим коэффициенты уравнения регрессии вида
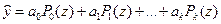 (IV.73)
(IV.73)
где
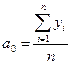 (IV.74)
(IV.74)
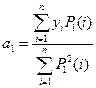 (IV.75)
(IV.75)
…………………
 (IV.76)
(IV.76)
Суммы, стоящие в знаменателе, можно определить по сокращенной формуле:
 (IV.77)
(IV.77)
где  – произведение всех нечетных чисел от 1 до
– произведение всех нечетных чисел от 1 до  включительно. В частности,
включительно. В частности,
 (IV.78)
(IV.78)
 (IV.79)
(IV.79)
 (IV.80)
(IV.80)
 (IV.81)
(IV.81)
Эти суммы используются и для вычисления сумм 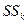 , нужных для определения остаточной дисперсии:
, нужных для определения остаточной дисперсии:
 (IV.82)
(IV.82)
После получения уравнения регрессий (IV.73) переменную z опять заменяют первоначальной переменной х.
Пример 2. Требуется определить зависимость степени диссоциации а иодида водорода от температуры t. Экспериментальные данные приведены ниже:
t,0С.... 280 300 320 340 360 380 400 420 440 460 480
a..... 0,178 0,182 0,186 0,191 0,196 0,202 0,207 0,213 0,220 0,228 0,236
Объем выборки  . Температура фиксировалась через равные интервалы 200
. Температура фиксировалась через равные интервалы 200 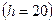 .
.
Решение. Применим метод ортогональных