При этом необходимо учитывать ошибки, возникающие при измерении характеристик объекта.
Требуется построить зависимость (модель)
W = f (x),
которая описывает характеристики изучаемой системы.
Это уравнение называется уравнением регрессии и описывает поверхность (гиперповерхность) отклика, характеризующую эмпирическую модель.
Обычно предполагается, что имеющиеся экспериментальные данные дают достаточно информации для воссоздания математического описания объекта.
На рис. 2.2 показано решение задачи идентификации для некоторого набора данных, полученное с помощью линейной регрессионной зависимости:
W= a + bx.
Идентификацию модели начинают с выбора формы модели, т.е. вида f (x).
При этом на практике может встретиться два случая:
1)
 |
Форма математической модели известна заранее, а задача идентификации сводится к определению коэффициентов этой модели. Так, описание ряда затухающих или развивающихся процессов дается зависимостями экспоненциального типа (Рис.2.3). Задача исследования - определение коэффициентов a, b.
2) Форма математической модели заранее неизвестна. В этом случае для идентификации модели используются отрезки бесконечных рядов, а задача заключается в определение числа членов ряда и коэффициентов при этих членах. Модель может быть представлена в виде:
,
где fq (xi) – некоторые заданные функции; b qi – коэффициенты регрессии; q = 0, 1,…, l.
В одномерном случае (k = 1) уравнение принимает вид:
.
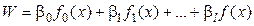Конкретный вид модели зависит от выбора функций fq (x), по которым производится разложение W. Например, при описании колебательных процессов удобно использовать ряд Фурье:
(Рис. 2.4).
Часто в качестве функций f 0(x), f 1(x), f 2(x),…, fl (x) выступают степенные функции: х 0, х 1, х 2,…, хl. Если ограничиться первыми членами разложения, то уравнения сведутся к линейным, квадратичным и другим полиномиальным моделям.
Обычно берут количество экспериментальных точек значительно больше, чем количество коэффициентов регрессии. В этом случае нельзя построить поверхность отклика, проходящую через все экспериментальные точки. Да этого и не требуется. При этом, однако, можно построить приближенную модель, обеспечивающую в некотором смысле наилучшее совпадение с экспериментальными данными.
Например, прямая a построена по 10-ти экспериментальным точкам методом наименьших квадратов (Рис.2.5); кривая b – квадратичная модель; с – полиномиальная модель 3-го порядка достаточно хорошо соответствует исходному экспериментальному материалу, хотя проходит не через все экспериментальные точки.
Таким образом, для любой экспериментальной выборки могут быть предложены различные модели идентификации. Конкретная форма модели зависит от выбора функций fq(x) и количества членов ряда.
Сама постановка задачи идентификации включает в себя элемент неопределенности, возможность множественности решений. Важно выбрать лучшее или, по крайней мере, достаточно хорошее из этих решений.
Для оценки точности модели естественно использовать величины отклонений, полученных в эксперименте величин Wi и их оценок Wmi, предсказанных моделью:
e j = Wi – Wmi.
Исключительное распространение получил метод наименьших квадратов отклонений реальных значений оцениваемой величины от значений, предсказанных моделью.
Задание 2.2. Провести идентификацию эмпирической математической модели.
А) Предполагается, что процесс описывается одномерным уравнением 2-го порядка:
W = a 0 + a 1 x + a 2 x 2, 0 £ x £ 10.
Б) Предполагается, что процесс описывается одномерным уравнением 3-го порядка:
W = a 0 + a 1 x + a 2 x 2+ a 3 x 3 0 £ x £ 10.
Считаем, что величина х измеряется точно, а W – с ошибкой e, имеющей нормальное распределение с нулевым математическим ожиданием и единичной дисперсией М (e) = 0, s2(e) = 1. Проверить адекватность модели методом Фишера и сравнить модели А) и Б) графически с моделью линейной регрессии.
Исходные данные: Таблица 2.1
| i | |||||||||||
| x | |||||||||||
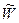
| 20,81 | 33,95 | 40,39 | 50,6 | 59,3 | 59,7 | 56,1 | 86,8 | 73,9 | 94,6 |
Решение:
А) Предполагается, что процесс описывается одномерным уравнением 2-го порядка
Wm2 = a 0 + a 1 x + a 2 x 2, 0 £ x £ 10.
Таблица 2.2
| i | x |  (Wv)
| W m2(Wm2) | e |
| 20,81 | 24,511 | -3,701 | ||
| 33,95 | 32,098 | 1,852 | ||
| 40,39 | 39,601 | 0,789 | ||
| 50,6 | 47,02 | 3,58 | ||
| 59,3 | 54,355 | 4,945 | ||
| 59,7 | 61,606 | -1,906 | ||
| 56,1 | 68,773 | -12,673 | ||
| 86,8 | 75,856 | 10,944 | ||
| 73,9 | 82,855 | -8,955 | ||
| 94,6 | 89,77 | 4,83 | ||
| 96,601 | 0,399 |
Метод наименьших квадратов заключается в том, что неизвестные (искомые) коэффициенты а0, а1, а2 должны минимизировать функцию, представляющую собой сумму квадратов невязок ei:
.
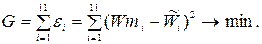Минимум некоторой функции, как известно, находится в точке 
, где все частные производные этой функции по переменным а 0, а 1, а 2равны нулю.
Введем исходные данные в программе Maxima:
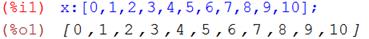
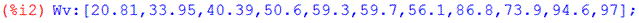
Для определения частных производных, распишем функцию G через её предполагаемый вид:
.
Возьмём от функции G производные по а 0, а 1, а 2:
;
;
.
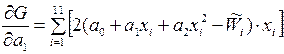Приравняв эти производные нулю и произведя некоторые преобразования, получим систему линейных алгебраических уравнений третьего порядка с тремя неизвестными.
Для решения этой системы вычисляем все производные и указанные в ней суммы по известным данным из табл. 2.1.
Решаем полученную систему в программе Maxima:
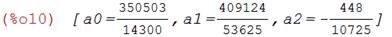
Коэффициенты а 0, а 1, а 2:
а 0=24,511; а 1=7,629; а 2 = –0,042.
Таким образом, математическая модель будет иметь вид:
Wm = 24,511+ 7,629 x – 0,042 x 2. (1)
Проверим адекватность модели методом Фишера. Подставляя в математическую модель (1) заданные значения x i, заполним четвёртый и пятый столбцы таблицы 2.2.
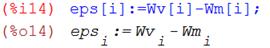
Определим число степеней свободы системы по формуле
fs = n – m – 1,
где n= 11 – количество экспериментальных точек; m = 3 – количество неизвестных коэффициентов. То есть fs = 11 – 3 – 1 = 7.
Выборочная дисперсия вычисляется по формуле:
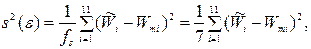
Критерий Фишера вычисляется по формуле:
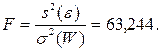
По статистическим таблицам при 5%-м уровне риска (a = 0,05) находим пороговое значение критерия Фишера
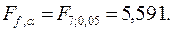
Так как полученное значение F больше критического (порогового), гипотеза об адекватности модели реальному процессу не принимается.
Б) Предполагается, что процесс описывается одномерным уравнением 3-го порядка:
W = a 0 + a 1 x + a 2 x 2+ а 3 х 3, 0 £ x £ 10.
Таблица 2.3
| i | x | (Wv)
| W m3(Wm3) | e |
| 20,81 | 21,736 | -0,926 | ||
| 33,95 | 32,653 | 1,297 | ||
| 40,39 | 41,636 | -1,246 | ||
| 50,6 | 49,147 | 1,453 | ||
| 59,3 | 55,648 | 3,652 | ||
| 59,7 | 61,601 | -1,901 | ||
| 56,1 | 67,468 | -11,368 | ||
| 86,8 | 73,711 | 13,089 | ||
| 73,9 | 80,792 | -6,892 | ||
| 94,6 | 89,173 | 5,427 | ||
| 99,316 | -2,316 |
Введем исходные данные в программе Maxima:
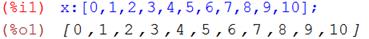
В случае кубической зависимости Wm3 = a 0 + a 1 x + a 2 x 2+ а 3 х 3, имеем:
.
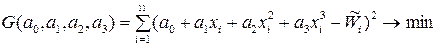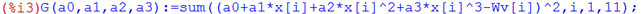
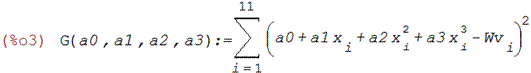
Возьмём от функции G производные по а 0, а 1, а 2, а 3:
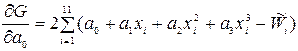
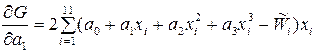
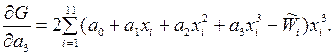
Приравняв их нулю и произведя некоторые преобразования, получим нормальную систему уравнений следующего вида:
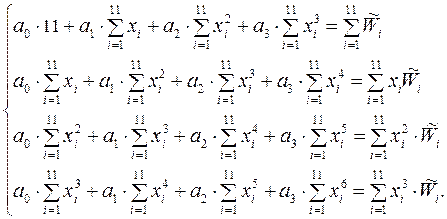
Для составления этой системы вычисляем все производные и указанные в ней суммы по известным данным из табл. 2.1.
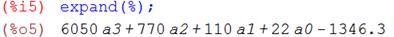
G 0 = -1346,3 + 22 a 0 +110 a 1 + 770 a 2 + 6050 a 3.
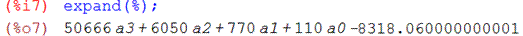
G 1 = -8318,06 + 110 a 0 +770 a 1 + 6050 a 2 + 50666 a 3
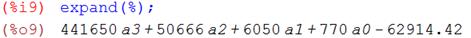
G 2 = -62914,42 + 770 a 0 +6050 a 1 + 50666 a 2 + 441650 a 3.
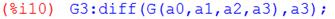
G 3 = -517342,34 + 6050 a 0 +50666 a 1 + 441650 a 2 + 3956810 a 3.
Решая полученную систему в программе Maxima, получим:
Коэффициенты а 0, а 1, а 2, а 3:
а 0=21,736; а 1=12,038; а 2 = –1,198, а 3= 0,077.
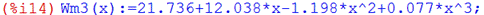
Математическая модель будет иметь вид:
Wm3= 21,736 + 12,038 x -1,198 x 2 + 0,077 х 3. (2)
Проверим адекватность модели методом Фишера. Подставляя в математическую модель (2) заданные значения x i, заполним четвёртый и пятый столбцы таблицы 2.3.
Определим число степеней свободы системы по формуле:
fs = n – m – 1,
где n= 11 – количество экспериментальных точек; m =4 – количество неизвестных коэффициентов, т.е. fs = 11 – 3 – 4 = 6.
Выборочная дисперсия вычисляется по формуле:
Критерий Фишера вычисляется по формуле:
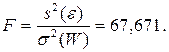
По статистическим таблицам при 5%-м уровне риска (a = 0,05) находим пороговое значение критерия Фишера
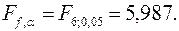
Так как полученное значение F больше критического (порогового), гипотеза об адекватности модели реальному процессу не принимается.
Проведём графически сравнение моделей квадратной и кубической с помощью линейной регрессии.
А) Модель квадратная:
Wm2 = 24,511+ 7,629 x – 0,042 x 2.
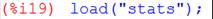
Рис.2.2.А. Модель квадратная
Б) Модель кубическая:
Wm3= 21,736 + 12,038 x -1,198 x 2 + 0,077 х 3.
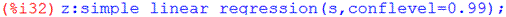
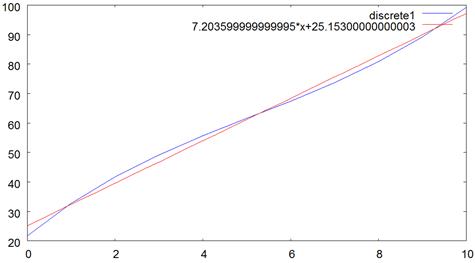
Рис.2.2.Б. Модель кубическая
Выводы: Как видно из графика: модель квадратная практически совпадает с линейной регрессией, а модель кубическая имеет небольшие отклонения от линии регрессии, значит, обе модели адекватны описываемому процессу.
Ответ:
А) Wm2 = 25,75+ 7,011 x – 0,06 x 2;
Б) Wm3= 21,736 + 12,038 x -1,198 x 2 + 0,077 х 3.