В чем сложность приема письменного деления на двух и трехзначные числа? Укажите последовательность изучения частных случаев деления, которые рассматриваются в учебниках математики начальных классов при знакомстве учащихся с алгоритмом письменного деления на 2-х и 3-хзначное число. Приведите рассуждения учеников в каждом из названных случаев.
Деление на двузначные и трёхзначные разрядные числа. Подготовкой к введению новых приёмов деления будет повторение приёмов деления без остатка на 10, 100 и 1000, введение приёмов деления с остатком на эти числа, а также изучение свойства деления числа на произведение.
Пусть требуется разделить:
Первое неполное делимое-498 дес., значит, в частном будет 2 цифры. Узнаем, сколько десятков будет в частном: разделим 498 на 10 и полученное частное 49 разделим на 6, поучится 8. Узнаем сколько десятков разделили: умножим 60 на 8, получится 480. Узнаем, сколько десятков осталось разделить: вычтем 480 из 498, получится 18. Нельзя 18 десятков разделить на 60 так, чтобы получились десятки, значит, цифра десятков подобрана правильно. Образуем второе неполное делимое: 18 дес-это 180 ед.
При делении многозначных чисел на двузначное и трёхзначное число пользуются свойством деления суммы на число. Для нахождения цифр частного пользуются приёмом замены делителя разрядным числом.
Приознакомление с делением на двузначное число сначала решаются примеры на деление без остатка и с остатком трёхзначных чисел, когда цифру частного находят в результате одной пробы и когда в частном получают однозначное число. Здесь ученики знакомятся с приёмом замены делителя ближайшим разрядным числом. 315:63.
Чтобы найти цифру частного, заменим делитель ближайшим меньшим разрядным числом 60 и будем делить 315 на 60, для этого достаточно разделить 31 на 6, получим 5. Цифра 5 не окончательная а пробная, потому что надо было 315 делить на 63, а не на 60. Цифру 5 проверим: умножим 63 на 5 (устно), получим 315, значит, цифра 5 верна.
Далее рассматриваются случаи деления четырёх-, пяти- и шестизначных чисел на двузначные, когда цифра частного получается в результате одной пробы.
Опыт показывает, что при письменном делении на двузначное число целесообразнее в большинстве случаев заменять делитель ближайшим меньшим разрядным числом. При этом меньше изменений вносить в делитель: сохраняется число десятков, изменяется только число простых единиц.
Приём деления на трёхзначное число аналогичен приёму деления на двузначное. Например, при делении на 643 делитель заменяем числом 600 и цифры частного находим путём последовательного деления числа на 100 и на 6. Цифра частного проверяется устно, и в этом основная трудность деления. Можно объяснить детям, что при трёхзначном делителе нет надобности умножать на цифру частного всё трёхзначное число. Достаточно умножить только две цифры высших разрядов и сопоставить полученный результат с неполным делимым. Такого рода устные вычисления учащимся доступны.
Навыки письменного деления, особенно деления на двузначное и трёхзначное число, являются сложными.
Теоретическая основа: 1) алгоритм письменного деления на однозначное и круглое число, 2) алгоритм письменного вычитания, 3) свойство деления суммы на число.
На подготовительном этапе повторяют теоретическую основу.
Затем на специальном уроке знакомят с приёмом деления на двухзначное число.
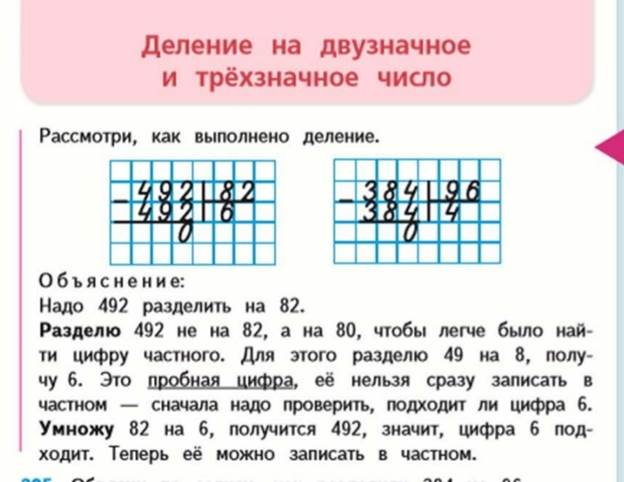
Для этого используют тот же алгоритм, что на 1 и 2 этапах, но в процессе рассуждения меняется этап подбора цифры частного. Он усложняется, т.к. делят, например, на 82 и в уме это сделать очень сложно, поэтому округляют 82 до 80 и сначала делят на 10, потом на 8. Цифру частного называют пробной цифрой.
Сначала разбирают наиболее простые случаи, когда:
а) в частном получается однозначное число, причем число проб равно 1,
М4М ч.2, стр.57
т.е. пробная цифра сразу подходит.
б) в частном получаем двузначное число, но число проб равно 1.

М4М ч.2, стр.59
в) вводим понятие «пробная цифра частного», т.е. рассматриваем случаи, когда при округлении делителя получаем такую цифру, которая не подходит, следовательно, её нужно либо увеличить, либо уменьшить. Её называют пробной цифрой.

М4М ч.2, стр.61
г) деление на трёхзначное число, когда в частном одна цифра и число проб равно 1.

М4М ч.2, стр.72
д) деление на трёхзначное число в частном две цифры и число проб равно 1.

М4М ч.2, стр.73
е) деление на трёхзначное число, когда число проб больше 1

М4М, ч.2, стр. 73
Далее до конца 4 класса отрабатывают вычислительные умения и навыки по данной теме.
Рассмотрим данные случаи в различных учебниках:
а) в частном получается однозначное число, причем число проб равно 1.

М4А ч.1, стр.128
б) в частном получаем двузначное число, но число проб равно 1.

М4А ч.1, стр.132

М4П ч.1, стр.37
в) вводим понятие «пробная цифра частного», т.е. рассматриваем случаи, когда при округлении делителя получаем такую цифру, которая не подходит, следовательно, её нужно либо увеличить, либо уменьшить. Её называют пробной цифрой.

М4А ч.1, стр.126
г) деление на трёхзначное число, когда в частном одна цифра и число проб равно 1.
Данного случая нет в других учебниках.
д) деление на трёхзначное число в частном две цифры и число проб равно 1.

М4А ч.1, стр.134
е) деление на трёхзначное число, когда число проб больше 1

М4А ч.1, стр.130

М4Д, ч.3, с.32
(случай, когда при округлении делителя получаем такую цифру, которая не подходит, следовательно, её нужно либо увеличить)

М4Д, ч.3, с.34
(в частном получаем двузначное число, но число проб равно 1)

М4Д, ч.3, с.46
(936: 312 - деление на трёхзначное число, когда в частном одна цифра и число проб равно 1)
(1024:128 - деление на трёхзначное число, когда число проб больше 1)
По программе Демидовой вводят 4 случая.