Свойство монотонности: АÍВ Þ d(A) £ d(B) для любых конечных упорядоченного множества В и его непустого подмножества А.
Доказательство:
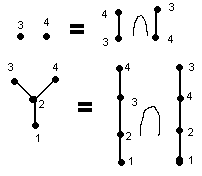
Пусть < B, ≤ >- конечное упорядоченное множество размерности n. Имеем, 
для линейных порядков £i на В. На подмножестве А рассмотрим индуцированный порядок 
из В, т.е. ограничение отношения £ на А.
Рассмотрим ограничения линейных порядков £i на А – они также линейны и в пересечении дадут порядок .
Значит, по определению размерности упорядоченного множества размерность <A, > не превосходит n.
Ч.т.д.
Свойство размерности дизъюнктивного объединения: Пусть А и В – конечные упорядоченные множества и X=A 
B. Тогда d(X)=max(d(A), d(B)), если хотя бы одно из множеств А или В не является цепью, и d(X)=2, если А и В – цепи.
Доказательство:
Дизъюнктивным объединением упорядоченных множеств А и В (А 
В) называется упорядоченное множество, состоящее из непересекающихся объединяемых множеств, на каждом из которых сохраняется свой порядок, а элементы из разных множеств попарно несравнимы.
Пусть <A, £> и <B, > - конечные упорядоченные множества.
Порядок на А 
для линейных порядков £i, а порядок на В 
для линейных порядков 
.
Пусть для определённости n³m и n³2.
В результате объединения А и В получается упорядоченное множество, состоящее из всех элементов А и всех элементов В. Значит, одному линейному порядку на А В соответствует два линейных порядка: один для А £i и один для В . Линейные порядки на А В должны содержать все n линейных порядков £i и все m линейных порядков , чтобы в пересечении они дали множество А 
В.
Первый линейный порядок на А Вопределим следующим образом:
£1 … 
.
Т.е. мы взяли первый линейный порядок на А и приписали к нему справа первый линейный порядок на В.
Второй линейный порядок на А Вполучим, взяв из множества А линейный порядок £2, а из множества В, если m³2, то линейный порядок 
, если же m=1, то линейный порядок 
. Но сейчас линейный порядок из множества А поместим за линейным порядком из множества В, для того, чтобы элементы из разных множеств были попарно несравнимы:
… £2, где j=1 при m=1 и j=2 при m³2.
Аналогичным образом будем получать остальные линейные порядки на А В:
£i …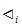 
при i£m
£i …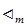 
при i>m.
Получим n линейных порядков, пересечение которых даёт множество А В. Т.е.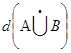 
=n=max(d(A), d(B)).
Ч.т.д.
Теорема 2. Размерность прямого произведения двух конечных упорядоченных множеств А и В меньше либо равна сумме их размерностей:
.
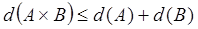Доказательство:
Дадим сначала несколько определений.
Пусть даны конечные упорядоченные множества <А, £> и <В, £>, размерности которых соответственно равны m и n. Поэтому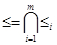 
, для некоторых линейных порядков £i на А и 
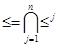для линейных порядков на В.
Определим покоординатно порядок на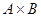 
:
(a, b)<(c, d) Û (a < c и b £ d) или (a £ c и b < d).
Определим m линейных порядков на 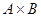по первой компоненте:
(a, b)<i(c, d) Û a<i c или (a=c и b<1 d) для i=1,…,m. (*)
Аналогично определим n линейных порядков на 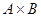по второй компоненте:
(a, b)<j(c, d) Û b<j d или (b=d и a<1 c) для j=1,…,n. (**)
Исходя из этих определений, порядок на 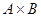можно определить и следующим образом:
(a, b)<(c, d)Û(a<ic и b£j d) или (a£I c и b<j d) (***)
для i=1,…,m и для j=1,…,n.
Для завершения доказательства достаточно показать, что имеет место равенство:
Тогда по определению размерности конечного упорядоченного множества получим 
.
Требуется доказать, что для любых (a,b) и (c,d) из :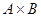
(a, b)<(c, d) Û(a, b)<i(c, d) и (a, b)<j(c, d).
Для " (a,b) и (c,d) из 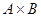не умоляя общности, будем считать, что
(a, b)<(c, d)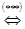 
(a<I c и b£j d) или (a£I c и b<j d) для i=1,…,m и для j=1,…,n.
Отсюда вследствие того, что x£y выполняется тогда и только тогда, когда x<y или x=y, следует равносильность:
Û(a<I c и b<j d) или (a<I c и b=d) или (a=c и b<j d)
для i=1,…,m и для j=1,…,n
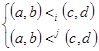
для i=1,…,m и для j=1,…,n.
Эта система равносильна тому, что элементы (a,b) и (c,d) сравнимы как по первой, так и по второй компоненте. И порядок на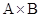 
равен пересечению его линейных порядков.
А т.к. размерность – это наименьшее число линейных порядков, дающих в пересечении множество, то 
.
Ч.т.д.
Теорема 3. Если А и В – не одноэлементные множества, причём А- решётка, а В –цепь, то размерность их прямого произведения на единицу больше размерности решётки:
.
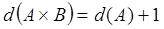Доказательство:
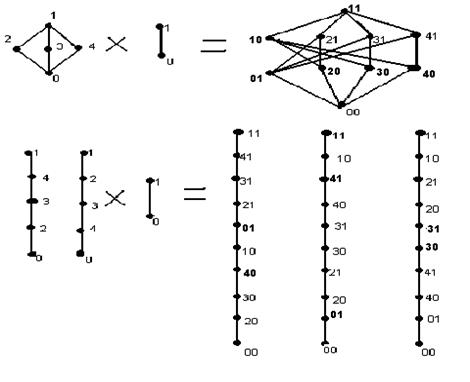
(по теореме 2).
Покажем, что выполняется и 
.
Возьмём любую цепь Z из множества цепей, пересечение которых образует решётку. Каждой такой цепи (а их 
) во множестве цепей, пересечение которых образует множество 
, будет соответствовать своя цепь, все первые компоненты которой находятся в таком же соответствии, как и элементы цепи Z.
Но во множестве среди вторых компонент должны сохраняться и соотношения, которые присутствуют в цепи В. Значит, во множестве цепей, пересечение которых образует множество , появится еще одна цепь.
Ч.т.д.
Теорема 4. 
решётка X, размерности n.
Доказательство:
Возьмём n не одноэлементных цепей А1, А2,…,Аn и рассмотрим множество X=A1 
A2 … An= 
. (n-1) раз применяя теорему 3 получаем, что d(X)=n.
Ч.т.д.
Теорема 5. Размерность множества всех подмножеств ß(M) множества М равна мощности множества М, т.е.
d(ß(M))= 
.
Доказательство:
1) Покажем, что ß(M) @ 
, где D={0,1}.
- будем рассматривать, как множество n-ок, состоящих из 0 и 1.
М={1,2,3,…,n}.
2) Чтобы доказать, что ß(M) и изоморфны, нужно установить взаимно однозначное соответствие.
Т.е. нужно показать, что для любого подмножества X множества М существует n-ка, состоящая из 0 и 1. И для любой n-ки существует подмножество Y множества М.
3) Выделим во множестве М подмножество X и составим по нему n-ку таким образом:
на место 1-ой компоненты n-ки поставим 1, если первый элемент множества М входит и в его подмножество X;
и 0, если 1-ый элемент множества М не входит в подмножество X.
Аналогичным образом определим все остальные компоненты n-ки.
Из нашего примера:
X (0,1,1,0,1,0…0)
n компонент
4) И, наоборот, возьмём произвольную n-ку. Например, (0,1,0,1,0…0). И поставим ей в соответствие подмножество Y множества М по тому же принципу:
если к-ая компонента равна 1, то к-ый элемент множества М входит в подмножество Y;
если же к-ая компонента равна 0, то к-ый элемент множества М не входит в подмножество Y.
Из примера получаем подмножество Y={2,4}.
5) Т.о. из ß(M)@ следует, что d(ß(M))=d() 
n
Получили, что d(ß(M))= 
.
Ч.т.д.
Литература
1. Беран Л. Упорядоченные множества: Популярные лекции по математике. Вып. 55. – М.: Наука, 1981.
2. Биркгоф Г. Теория решёток. – М.: Наука, 1984.
3. Вечтомов Е. М. Теория решёток: учебно-методическая разработка спецкурса. – Киров: КГПИ, 1995.
4. Гретцер Г. Общая теория решёток. – М.: Мир, 1982.
5. Оре О. Теория графов. - М.: Наука, 1980.