Ответ: 2r.
Задача 2: (Демонстрационный вариант ГИА 2013г.)
Основание АС равнобедренного треугольника АВС равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания АС. Найдите радиус окружности, вписанной в треугольник АВС.
Дано: Равнобедренный треугольник АВС, АС=12, Вневписанная окружность радиусом 8. Вписанная в треугольник окружность.(Рис.5).
Найти: Найдите радиус окружности, вписанной в треугольник АВС.
Решение:
Пусть О центр, ОМ радиус вневписанной окружности.О2 – центр, О2Н- радиус вписанной окружности.(Рис.5). ОМ=8.
По свойству вневписанной окружности, центр окружности лежит на пересечении биссектрис внешних углов, поэтому <МАО=<ОАС. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника АВС => <ВАО2=<О2АС => треугольник ОАО2 – прямоугольный. ВТ –перпендикуляр к АС, т.к. биссектриса в равнобедренном треугольнике является высотой => АТ - высота прямоугольного треугольника ОАО2.
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой => АТ2=ТО2∙ТО, ТО2=  => Т О2 = 4,5
=> Т О2 = 4,5
Ответ: 4,5
Задача 3 (Пробный ЕГЭ от 18.12 2013г.)[6]
Радиусы двух вневписанных окружностей прямоугольного треугольника 7 и 17. Найти расстояние между их центрами.
Случай1: одна из окружностей касается гипотенузы, а другая –катета.
Дано: Треугольник АВС- прямоугольный, <В=900. Вневписанные окружности (О1;r) и (О2;R), где r-7см, R-17.(Рис.6).
Найти: О1О2
Решение:
МС=ВМ+ВС=7+17=24. О1К=МС=24, О2К= 17-7=10. Из прямоугольного
∆О1КО2 по теореме Пифагора: О1О2=  см.
см.
Случай 2: обе окружности касаются катетов (Рис.7).
Решение:
Найдём диагонали квадратов: О1В=  см, О2В=
см, О2В= 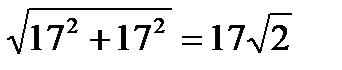 см.
см.
О1О2=7  +17
+17  =24
=24  см.
см.
Ответ. 26см и 24  см.
см.
Свойства вневписанной окружности
1. Каждый из отрезков касательных, проведённых из вершины треугольника, противоположной стороне касания вневписанной окружности, равен полупериметру треугольника.
Дано: Треугольник АВС (Рис.8). Вневписанная окружность с центром в точке О касается стороны ВС.
Доказать:
1. МВ=ВК, КС=СN. 2. AM=AN=p, где р - полупериметр треугольника АВС.
Доказательство.
Понадобится теорема о касательных: «Отрезки касательных, проведённых из одной точки к одной окружности, равны».
Из точки А проведены к одной окружности две касательные, значит, АМ=АN. Аналогично МВ=ВК, СN=КС, как отрезки касательных к этой же окружности соответственно из точек В и С. Получим: АМ=АВ+МВ, АN=АС+СN, АМ+АN=АВ+МВ+АС+СN=(АВ+АС)+(МВ+СN)=
(АВ+АС)+(ВК+КС)=АВ+АС+ВС=Р. Получим: АМ= АN=р.
Итак, каждый из отрезков касательных, проведённых из вершины треугольника, противоположной стороне касания вневписанной окружности, равен полупериметру треугольника.
Следствие: BK=BM=AM–AB=p-c; CN=CK=AN–CN=p-b. (Рис.9).
2. Длины сторон треугольника, и радиусы вписанной и вневписанной окружностей, связаны соотношением:

Доказательство. На рисунке 10 вписанная и вневписанная окружности с центрами О и О1.
Точки О и О1 лежат на биссектрисе угла А. ОL и O1M - радиусы окружностей, проведённые в точку касания, значит ОL и O1M перпендикулярны одной прямой АМ  ОL и O1M параллельны, а треугольники АОL и АО1М подобны. Получим:
ОL и O1M параллельны, а треугольники АОL и АО1М подобны. Получим:  .
.
Т.к. OL=r, O1M=R, AM=p, р-а=AL то  , где а – длина стороны касания вневписанной окружности, R – радиус вневписанной окружности, r – радиус вписанной окружности, p- полупериметр треугольника.
, где а – длина стороны касания вневписанной окружности, R – радиус вневписанной окружности, r – радиус вписанной окружности, p- полупериметр треугольника.
3. Радиус вневписанной окружности, касающейся данной стороны треугольника, равен отношению площади треугольника к разности полупериметра и этой стороны: ra =  , rb=
, rb=  , rc=
, rc=  .
.
Дано: ▲АВС. Вневписанная окружность(Оа ; ra). Рисунок 11. Доказать ra = 
 Решение: S=SABC=SAOaC+SBOaC–SBOaC = ×(b+c–a)=ra×(p–a), ra=
Решение: S=SABC=SAOaC+SBOaC–SBOaC = ×(b+c–a)=ra×(p–a), ra=  .
.
 => Т О2 = 4,5
=> Т О2 = 4,5 см.
см. см, О2В=
см, О2В= 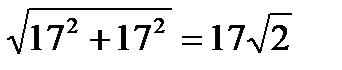 см.
см. +17
+17  =24
=24  см.
см. см.
см.
 ОL и O1M параллельны, а треугольники АОL и АО1М подобны. Получим:
ОL и O1M параллельны, а треугольники АОL и АО1М подобны. Получим:  .
. , где а – длина стороны касания вневписанной окружности, R – радиус вневписанной окружности, r – радиус вписанной окружности, p- полупериметр треугольника.
, где а – длина стороны касания вневписанной окружности, R – радиус вневписанной окружности, r – радиус вписанной окружности, p- полупериметр треугольника. , rb=
, rb=  , rc=
, rc=  .
.
 Решение: S=SABC=SAOaC+SBOaC–SBOaC = ×(b+c–a)=ra×(p–a), ra=
Решение: S=SABC=SAOaC+SBOaC–SBOaC = ×(b+c–a)=ra×(p–a), ra=  .
.