Диаграммы Венна (по аналогии с кругами Эйлера) – это схематическое изображение действий с множествами. Опять же предупреждаю, что я рассмотрю не все операции:
1) Пересечение множеств характеризуется логической связкой И и обозначается значком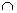 
Пересечением множеств 
и 
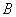называется множество 
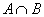, каждый элемент которого принадлежит и множеству , и множеству 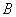. Грубо говоря, пересечение – это общая часть множеств:
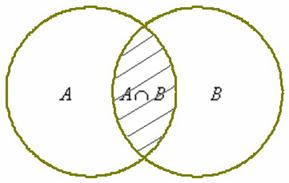
Так, например, для множеств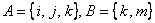 
:
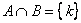
Если у множеств нет одинаковых элементов, то их пересечение пусто. Такой пример нам только что встретился при рассмотрении числовых множеств:
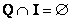
Множества рациональных и иррациональных чисел можно схематически изобразить двумя непересекающимися кругами.
Операция пересечения применима и для бОльшего количества множеств, в частности в Википедии есть хороший пример пересечения множеств букв трёх алфавитов.
2) Объединение множеств характеризуется логической связкой ИЛИ и обозначается значком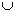 
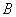Объединением множеств и называется множество 
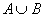, каждый элемент которого принадлежит множеству или множеству :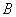
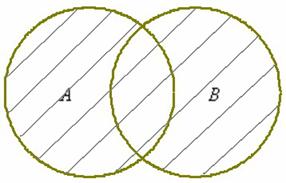
Запишем объединение множеств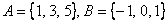 
:
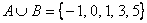– грубо говоря, тут нужно перечислить все элементы множеств и 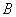, причём одинаковые элементы (в данном случае единица на пересечении множеств) следует указать один раз.
Но множества, разумеется, могут и не пересекаться, как это имеет место быть с рациональными и иррациональными числами:
В этом случае можно изобразить два непересекающихся заштрихованных круга.
Операция объединения применима и для бОльшего количества множеств, например, если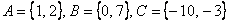 
, то:
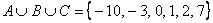, при этом числа вовсе не обязательно располагать в порядке возрастания (это я сделал исключительно из эстетических соображений). Не мудрствуя лукаво, результат можно записать и так:
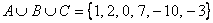
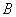3) Разностью множеств и называют множество 
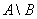, каждый элемент которого принадлежит множеству и не принадлежит множеству :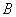
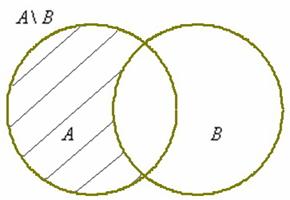
Разность 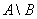читаются следующим образом: «а без бэ». И рассуждать можно точно так же: рассмотрим множества 
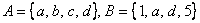. Чтобы записать разность 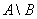, нужно из множества «выбросить» все элементы, которые есть во множестве :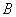
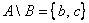
Пример с числовыми множествами:
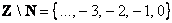– здесь из множества целых чисел исключены все натуральные, да и сама запись 
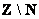так и читается: «множество целых чисел без множества натуральных».
Зеркально: разностью множеств 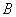и называют множество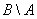 
, каждый элемент которого принадлежит множеству 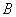и не принадлежит множеству :
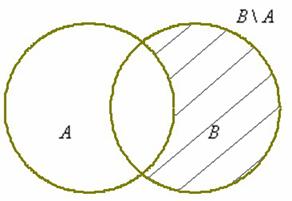
Для тех же множеств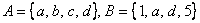
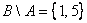– из множества 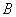«выброшено» то, что есть во множестве .
А вот эта разность оказывается пуста: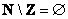 
. И в самом деле – если из множества натуральных чисел исключить целые числа, то, собственно, ничего и не останется:)
Кроме того, иногда рассматривают симметрическую разность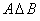 
, которая объединяет оба «полумесяца»:
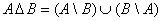– иными словами, это «всё, кроме пересечения множеств».
4) Декартовым (прямым) произведением множеств и 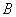называется множество 
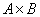всех упорядоченных пар 
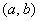, в которых элемент 
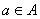, а элемент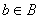 
Запишем декартово произведение множеств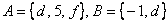 
:
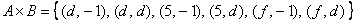– перечисление пар удобно осуществлять по следующему алгоритму: «сначала к 1-му элементу множества последовательно присоединяем каждый элемент множества 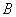, затем ко 2-му элементу множества присоединяем каждый элемент множества 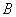, затем к 3-му элементу множества присоединяем каждый элемент множества »: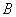
Зеркально: декартовым произведением множеств 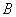и называется множество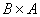 
всех упорядоченных пар 
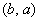, в которых 
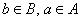. В нашем примере:
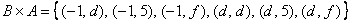– здесь схема записи аналогична: сначала к «минус единице» последовательно присоединяем все элементы множества , затем к «дэ» – те же самые элементы:
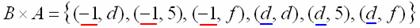
Но это чисто для удобства – и в том, и в другом случае пары можно перечислить в каком угодно порядке – здесь важно записать все возможные пары.
А теперь гвоздь программы: декартово произведение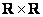 
– это есть ни что иное, как множество точек 
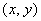нашей родной декартовой системы координат 
.
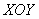Задание для самостоятельного закрепления материала:
Выполнить операции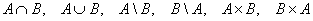 
, если:
1) 
;
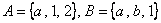2) 
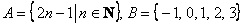
Множество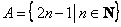 
удобно расписать перечислением его элементов.
И пунктик с промежутками действительных чисел:
3) 
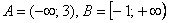
Напоминаю, что квадратная скобка означает включение числа в промежуток, а круглая – его невключение, то есть «минус единица» принадлежит множеству 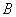, а «тройка» не принадлежит множеству . Постарайтесь разобраться, что представляет собой декартово произведение данных множеств. Если возникнут затруднения, выполните чертёж;)
Краткое решение задачи в конце урока.
Отображение множеств
Отображение множества во множество 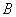– это правило, по которому каждому элементу множества ставится в соответствие элемент (или элементы) множества 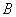. В том случае если в соответствие ставится единственный элемент, то данное правило называется однозначно определённой функцией или просто функцией.
Функцию, как многие знают, чаще всего обозначают буквой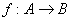 
– она ставит в соответствие каждому элементу 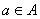единственное значение 
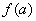, принадлежащее множеству .
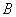Ну а сейчас я снова побеспокою множество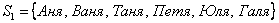 
студентов 1-го ряда и предложу им 6 тем для рефератов (множество 
):
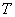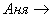Векторы
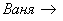Матрицы
Определители
Комплексные числа (о, да!)
Теория пределов
Что такое производная?
Установленное (добровольно или принудительно =)) правило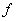 
ставит в соответствие каждому студенту 
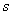множества 
единственную тему реферата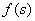 
множества .
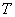…а вы, наверное, и представить себе не могли, что сыграете роль аргумента функции =) =)
Элементы множества образуют область определения функции (обозначается через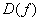 
), а элементы множества 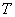– область значений функции (обозначается через 
).
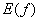Построенное отображение множеств имеет очень важную характеристику: оно является взаимно-однозначным или биективным (биекцией). В данном примере это означает, что каждому студенту поставлена в соответствие одна уникальная тема реферата, и обратно – за каждой темой реферата закреплён один и только один студент.
Однако не следует думать, что всякое отображение биективно. Если на 1-й ряд (к множеству ) добавить 7-го студента, то взаимно-однозначное соответствие пропадёт – либо один из студентов останется без темы (отображения не будет вообще), либо какая-то тема достанется сразу двум студентам. Обратная ситуация: если к множеству 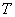добавить седьмую тему, то взаимнооднозначность отображения тоже будет утрачена – одна из тем останется невостребованной.
Уважаемые студенты на 1-м ряду, не расстраивайтесь – остальные 20 человек после пар пойдут прибирать территорию университета от осенней листвы. Завхоз выдаст двадцать голиков, после чего будет установлено взаимно-однозначное соответствие между основной частью группы и мётлами…, а Вольдемар ещё и в магазин сбегать успеет =)
Теперь разберёмся со «школьной» функцией одной переменной. Пожалуйста, загляните на страницу Функции и графики (отроется на соседней вкладке), и в Примере 1 найдите график линейной функции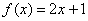 
.
Задумаемся, что это такое? Это правило 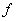, которое каждому элементу 
области определения (в данном случае это все значения «икс») ставит в соответствие единственное значение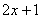 
. С теоретико-множественной точки зрения, здесь происходит отображение множества действительных чисел во множество действительных чисел:
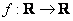
Первое множество мы по-обывательски называем «иксами» (независимая переменная или аргумент), а второе – «игреками» (зависимая переменная или функция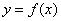 
).
Далее взглянем на старую знакомую параболу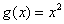 
. Здесь правило 
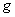каждому значению «икс» ставит в соответствие его квадрат, и имеет место отображение:
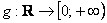
Итак, что же такое функция одной переменной? Функция одной переменной – это правило 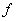, которое каждому значению независимой переменной из области определения ставит в соответствие одно и только одно значение .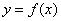
Как уже отмечалось в примере со студентами, не всякая функция является взаимно-однозначной. Так, например, у функции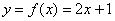 
каждому «иксу» области определения соответствует свой уникальный «игрек», и наоборот – по любому значению «игрек» мы сможем однозначно восстановить «икс». Таким образом, это биективная функция.
! На всякий случай ликвидирую возможное недопонимание: моя постоянная оговорка об области определения не случайна! Функция может быть определена далеко не при всех «икс», и, кроме того, может быть взаимно-однозначной и в этом случае. Типичный пример: 
А вот у квадратичной функции не наблюдается ничего подобного, во-первых:
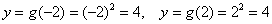– то есть, различные значения «икс» отобразились в одно и то же значение «игрек»; и во-вторых: если кто-то вычислил значение функции и сообщил нам, что 
, то не понятно – этот «игрек» получен при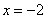 
или при 
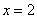? Что и говорить, взаимной однозначностью здесь даже не пахнет.
Задание 2: просмотреть графики основных элементарных функций и выписать на листок биективные функции. Список для сверки в конце этого урока.
Мощность множества
Интуиция подсказывает, что термин характеризует размер множества, а именно количество его элементов. И интуиция нас не обманывает!
Мощность пустого множества равна нулю.
Мощность множества 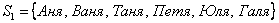равна шести.
Мощность множества букв русского алфавита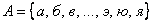 
равна тридцати трём.
И вообще – мощность любого конечного множества равно количеству элементов данного множества.
…возможно, не все до конца понимают, что такое конечное множество – если начать пересчитывать элементы этого множества, то рано или поздно счёт завершится. Что называется, и китайцы когда-нибудь закончатся.
Само собой, множества можно сравнивать по мощности и их равенство в этом смысле называется равномощностью. Равномощность определяется следующим образом:
Два множества являются равномощными, если между ними можно установить взаимно-однозначное соответствие.
Множество студентов равномощно множеству 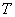тем рефератов, множество букв русского алфавита равномощно любому множеству из 33 элементов и т.д. Заметьте, что именно любому множеству из 33 элементов – в данном случае имеет значение лишь их количество. Буквы русского алфавита можно сопоставить не только с множеством номеров
1, 2, 3, …, 32, 33, но и вообще со стадом в 33 коровы.
Гораздо более интересно обстоят дела с бесконечными множествами. Бесконечности тоже бывают разными! ...зелёными и красными Самые «маленькие» бесконечные множества – это счётные множества. Если совсем просто, элементы такого множества можно пронумеровать. Эталонный пример – это множество натуральных чисел 
. Да – оно бесконечно, однако у каждого его элемента в ПРИНЦИПЕ есть номер.
Примеров очень много. В частности, счётным является множество всех чётных натуральных чисел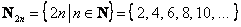 
. Как это доказать? Нужно установить его взаимно-однозначное соответствие с множеством натуральных чисел или попросту пронумеровывать элементы:
Взаимно-однозначное соответствие установлено, следовательно, множества равномощны и множество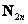 
счётно. Парадоксально, но с точки зрения мощности – чётных натуральных чисел столько же, сколько и натуральных!
Множество целых чисел тоже счётно. Его элементы можно занумеровать, например, так:
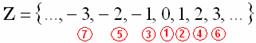
Более того, счётно и множество рациональных чисел 
. Поскольку числитель – это целое число (а их, как только что показано, можно пронумеровать), а знаменатель – натуральное число, то рано или поздно мы «доберёмся» до любой рациональной дроби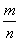 
и присвоим ей номер.
А вот множество действительных чисел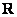 
уже несчётно, т.е. его элементы пронумеровать невозможно. Данный факт строго доказывается в теории множеств, но, в общем-то, он и так очевиден – во множестве 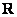содержится тьма иррациональных чисел с бесконечными дробными «хвостами», в которых не наблюдается никакой закономерности.
Мощность множества действительных чисел также называют континуумом, и по сравнению со счётными множествами это «более бесконечное» множество.
Поскольку между множеством 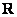и числовой прямой существует взаимно-однозначное соответствие (см. выше), то множество точек числовой прямой тоже несчётно. И более того, что на километровом, что на миллиметровом отрезке – точек столько же! Классический пример:
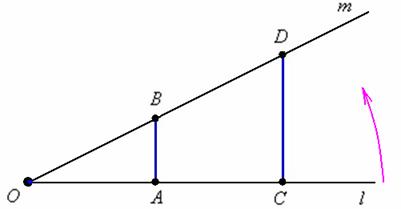
Поворачивая луч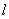 
против часовой стрелки до его совмещения с лучом 
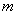мы установим взаимно-однозначное соответствие между точками синих отрезков. Таким образом, на отрезке 
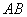столько же точек, сколько и на отрезке и 
!
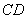Данный парадокс, видимо, связан с загадкой бесконечности… но мы сейчас не будем забивать голову проблемами мироздания, ибо на очереди основы математической логики, а не философия =)
Спасибо за внимание и успехов вам в учёбе!
Решение заданий:
Задание 1
1)
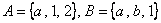
2)
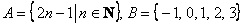
– это множество нечётных натуральных чисел: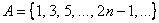 
3)
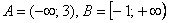
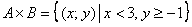– все точки 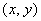координатной плоскости 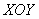, удовлетворяющие двум указанным неравенствам. Аналогично:
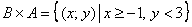
Задание 2 Взаимно-однозначные функции на иллюстрациях урока Функции и графики:
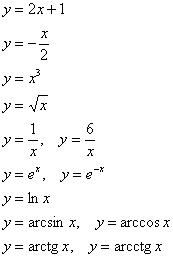
Автор: Емелин Александр