Позиционные и непозиционные системы счисления.

Понятие числа является фундаментальным как для математики, так и для информатики. С числами связано еще одно важное понятие — система счисления.

Система счисления — это способ изображения чисел и соответствующие ему правила действий над числами.

Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить нанепозиционные и позиционные.

В древние времена, когда люди начали считать, появилась потребность в записи чисел. Первоначально количество предметов отображали равным количеством каких-нибудь значков: насечек, черточек, точек.

Изучение археологами «записок» времен палеолита на кости, камне, дереве показало, что люди стремились группировать отметки по 3, 5, 7, 10 штук. Такая группировка облегчала счет. Люди учились считать не только единицами, но и тройками, пятерками и пр. Поскольку первым вычислительным инструментом учеловека были пальцы, поэтому и счет чаще всего вели группами по 5 или по 10 предметов.

В дальнейшем свое название получили десяток десятков (сотня), десяток сотен (тысяча) и так далее. Такие узловые числа для удобства записи стали обозначать особыми значками — цифрами. Если при подсчете предметов их оказывалось 2 сотни, 5 десятков и еще 4 предмета, то при записи этой величины дважды повторяли знак сотни, пять раз — знак десятков и четыре раза знак единицы.

В таких системах счисления от положения знака в записи числа не зависит величина, которую он обозначает; поэтому они называются непозиционными системами счисления.

Непозиционными системами пользовались древние египтяне, греки, римляне и некоторые другие народы древности.

На Руси вплоть до XVIII века, использовалась непозиционная система славянских цифр. Буквы кириллицы (славянского алфавита) имели цифровое значение, если над ними ставился специальный знак ~ титло. Например Ã — 1, 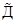— 4, 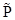— 100.

Непозиционные системы счисления были более или менее пригодны для выполнения сложения и вычитания, но совсем не удобны при умножении и делении.

Идея позиционной системы счисления впервые возникла в древнем Вавилоне.

В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции.

Количество используемых цифр называется основанием позиционной системы счисления.

Система счисления, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, так как запись любых чисел производится с помощью десяти цифр:

0,1, 2, 3, 4, 5, 6, 7, 8, 9.

Хотя десятичную систему принято называть арабской, но зародилась она в Индии, в V веке. В Европе об этой системе узнали в XII веке из арабских научных трактатов, которые были переведены на латынь. Этим и объясняется название «арабские цифры». Однако широкое распространение в науке и в обиходе десятичная позиционная система получила только в XVIвеке. Эта система позволяет легко выполнять любые арифметические вычисления, записывать числа любой величины. Распространение арабской системы дало мощный толчок развитию мате­матики.

С позиционной десятичной системой счисления вы знакомы с раннего детства, только, возможно, не знали, что она так называется.

Позиционный тип этой системы легко понять на примере любого многозначного числа. Например, в числе 333 первая тройка означает три сотни, вторая — три десятка, третья — три единицы. Одна и та же цифра в зависимости от позиции в записи числа обозначает разные величины.

 

333 = 3x100 + 3x10 + 3.

Еще пример:

32478 = 3 х 10000 + 2 х 1000 + 4 х 100 + 7 х 10 + 8 =

= 3 х 10⁴ + 2 х 10³ + 4 х 10² + 7 х 10¹ + 8 х 10⁰.

Отсюда видно, что всякое десятичное число можно представить как сумму произведений составляющих его цифр на соответствующие степени десятки. То же самое относится и к десятичным дробям.

26,387 = 2 х 10¹ + 6 х 10⁰+ 3 х 10^-1 + 8 х 10^-2 + 7 х 10^-3

Системы счисления, используемые в ЭВМ

Очевидно, число «десять» — не единственно возможное основание позиционной системы. Известный русский мате­матик Н.Н.Лузин так выразился по этому поводу: «Пре­имущества десятичной системы не математические, а зоо­логические. Если бы у нас на руках было не десять пальцев, а восемь, то человечество пользовалось бы восьмеричной системой».

За основание позиционной системы счисления можно принять любое натуральное число большее 1. Упомянутая выше вавилонская система имела основание 60. Следы этой системы сохранились до наших дней в порядке счета единиц времени (1 час = 60 мин, 1 мин = 60 с).

Для записи чисел в позиционной системе с основанием n нужно иметь алфавит из n цифр. Обычно для этого при n<10 используют n первых арабских цифр, а при n>10 к десяти арабским цифрам добавляют буквы.

Вот примеры алфавитов нескольких систем:

 

Основание	Система	Алфавит
n=2	двоичная
n=3	троичная	01 2
n=8	восьмеричная
n=16	шестнадцатеричная	0123456789ABCDEF

 

Основание системы, к которой относится число, обозначается подстрочным индексом к этому числу.

101101₂, 3671₈, 3B8F₁₆.

.

Принципы архитектуры ЭВМ были сформулированы Джоном фон Нейманом в 1946 году. Им долгие годы сле­довали конструкторы ЭВМ. Многие из этих принципов со­хранились и в архитектуре современных компьютеров.

Один из этих принципов Неймана:

ЭВМ выполняет арифметические расчеты в двоичной системе счисления.

Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

· для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;

· представление информации посредством только двух состояний надежно и помехоустойчиво;

· возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

· двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.

Гораздо проще сконструировать процессор, который ра­ботает в двоичной системе счисления, чем работающий в десятичной. Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Например:

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Например,

 

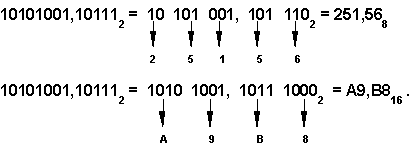
Шестнадцатеричная система счисления используется для компактного представления (на бумаге или на экране) двоичной информации, хранимой в памяти ЭВМ.

Алгоритмы перевода чисел из одной системы счисления в другую.

Мы настолько привыкли к десятичному счету, что число в любой другой системе мало что нам говорит о соответст­вующем ему количестве. Например, что за величина 112₃? Чтобы понять «много это или мало», нужно перевести его в десятичную систему. Сделать это довольно просто.

Число 112₃ содержит в себе 2 единицы, 1 тройку и 1 девятку. Как и в десятичной системе, число можно пред­ставить в виде суммы произведений составляющих его цифр на соответствующие степени основания системы (в нашем примере — тройки).

112₃ =1х3² + 1х3¹ + 2х3°= 9 + 3 + 2 = 14₁₀

Следовательно, 112₃ = 14₁₀

Переведем двоичное число 101101₂ в десятичную систему счисления. Принцип тот же. Теперь в сумму надо подстав­лять степени двойки:

101101₂= 1 х 2⁵ + 0 х 2⁴+ 1 х 2³ + 1 х 2² + 0 х 2¹ + 1x2°= 32+ 8 + 4 + 1 = 45₁₀.

И еще один пример — с шестнадцатеричным числом:

15FC₁₆ = 1 х 16³ + 5 х 16²+ 15 х 16¹ + 12 = 4096 + 1280 + 240 + 12 = 5628

 

Аналогично переводятся дробные числа.

101,11₂ = 1 х 2² + 0 х 2¹ + 1 х 2° + 1 х 2^-1 + 1 х 2^-2 =

= 4 + 1 + 1/2 + 1/4 = 5 + 0,5 + 0,25 = 5,75₁₀.

А как произвести обратный перевод из десятичной сис­темы в недесятичную (n≠10)? Для этого нужно суметь разложить десятичное число на слагаемые, содержащие сте­пени n. Например, при n = 2 (двоичная система):

15₁₀ = 8 + 4 + 2 + 1 = 1х2³ + 1х2²+ 1x2¹ + 1 = 1111₂

Эта задача уже посложнее, чем перевод в десятичную систему. Попробуйте, например, таким образом перевести в двоичную систему число 157. Конечно можно, но трудно!

Однако существует процедура, позволяющая легко выпол­нить такой перевод. Она состоит в том, что данное десятичное число делится с остатком на основание системы. Полученный остаток — это младший разряд искомого числа, а полученное частное снова делится с остатком, который равен второй спра­ва цифре и т.д. Так продолжается до тех пор, пока частное не станет меньше делителя (основания системы). Это частное — старшая цифра искомого числа.

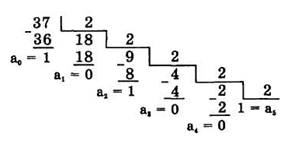
Продемонстрируем этот метод на примере перевода числа 37₁₀ в двоичную систему. Здесь для обозначения цифр в записи числа используется символика: а₅а₄а₃а₂а₁а₀.

Отсюда: 3710 - 1001012

 

 

Перевод правильной десятичной дроби в другую систему счисления производится путем последовательных умноже­ний на основание системы с выделением целой части произведений. Однако мы остановимся лишь на целых числах.

Двоичная арифметика.

Вам хорошо знакомы правила выполнения арифметичес­ких операций с многозначными десятичными числами. В младших классах школы вы учились складывать, вычитать, умножать «столбиком» и делить «уголком». В конечном счете для выполнения вычислений нужно уметь складывать и умножать однозначные числа. Таблицу умножения деся­тичных чисел многие первоклассники заучивают долго и с большим трудом. Но вот если бы в школе изучали не десятич­ную, а двоичную арифметику, проблем бы не было ни у кого и все ученики были бы отличниками! Сейчас вы убедитесь в том, что двоичная арифметика, действительно, очень проста.

С двоичной системой счисления вы уже знакомы. В ней всего две цифры: 0 и 1. Вот все варианты их сло­жения:

0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 10.

Вам уже должно быть понятно, что 10₂ = 2₁₀ (напомним, что нижний индекс обозначает основание системы счисления и всегда записывается в десятичной системе). Ряд двоичных натуральных чисел легко записать, получая каждое следую­щее число путем прибавления единицы к предыдущему.

Таблица 1. Десятичные числа от 1 до 16 и равные им двоичные числа

 

«10»	«2»	«10»	«2»	«10»	«2»	«10»	«2»

Из таблицы 1 видно, как быстро нарастает количество цифр в двоичных числах. Но этот недостаток двоичной сис­темы компенсируется простотой арифметики. Вот пример сложения столбиком двух многозначных двоичных чисел:

1 0 1 1 0 1 1 1 0 1

⁺ 1 1 1 0 1 0 1 1 0

1 0 0 1 0 1 1 0 0 1 1

Двоичная таблица умножения:

0 x 0 = 0, 1 x 0 = 0, 1 x 1 = 1.

Пример:

^х11

111

⁺ 111

10101

 

Вопросы самоконтроля

 

1. В чем отличие позиционной и непозиционной систем счисления?

2. Что такое система счисления?

3. Что такое основание системы счисления?

4. Что такое непозиционная система счисления?

5. Что такое позиционная система счисления?

6. Из каких знаков состоит алфавит десятичной и двоичной систем?

7. Почему в вычислительной технике взята за основу двоичная система счисления?