Системы линейных сравнений по модулю. Китайская теорема об остатках

Определение 1. Системой m линейных cравнений с n неизвестными x ₁, x ₂,…, x_n (СЛCУ) называется система cравнений вида:

(1)

где a ₁₁, a ₁₂,..., a_kn, b ₁, b ₂,..., b_m - фиксированные целые числа, m ₁,…, m_k – натуральные числа.

Определение 2. Решением системы сравнений (1) называется такой вектор , состоящий из классов вычетов по некоторому модулю m, для которого любой вектор целых чисел

удовлетворяет всем сравнениям системы (1).

Рассмотрим сначала случай, когда все модули m ₁,…, m_k в системе (1) равны и система (1) имеет вид:

(2)

Если p простое число, то множество классов вычетов Z _p по модулю p является полем и для системы сравнений применимы все методы решений и основные теоремы, которые имеют место для теории СЛУ над полем.

Пример 1. Решить СЛС

Способ 1. Метод Гаусса:

Все операции выполняются по модулю 7 или в роле Z ₇.

Способ 2. Правило Крамера:

Тогда система равносильна системе

Ответ: .

В общем случае для решению системы сравнений вида (2) можно применить методы, изложенные в лекции 2 для решения систем линейных диофантовых уравнений, учитывая следующие замечания:

Нельзя умножать или делить сравнения системы на числа, которые не взаимно простые с модулем, так как при этом может получиться не равносильная система сравнений. Такие преобразования системы назовем элементарными целочисленными приведенными преобразованиями.

Определение 3. Целая матрица D = (d_ij) размерности m ´ n называется матрицей канонического вида, если она обладает свойствами:

1) все элементы d_ij = 0 для любых i = 1, 2,…, m; j = 1, 2,…, n; i ¹ j;

2) все элементы d_ij ³ 0 для любых i = 1, 2,…, k, где k = min { m. n };

3) d_ii | d_{i+ 1, i+ 1} для любых i = 1, 2,…, k- 1, где k = min { m, n }.

Элементы d_ij, i = 1, 2,…, k, где k = min { m, n }, называем диагональными элементами канонической матрицы. Обозначим число ненулевых диагональных элементов канонической матрицы через r. Очевидно, что r = rang D.

Теорема 1. Любую целую матрицу конечным числом целочисленных приведенных элементарных преобразований строк и столбцов можно привести к матрице канонического вида, при этом r = rang A.

Диагональные элементы d ₁₁,…, d_rr, r = rang A, матрицы канонического вида, эквивалентной матрице A, называются элементарными делителями матрицы A.

Теорема 2. Система ЛC (2) разрешима тогда и только тогда, когда НОД (d_ii, m), элементарных делителей d_ii матрицы A делит соответствующие элементарные делители расширенной матрицы СЛС. 

Пример 2. Выяснить разрешимость данной СЛС

Решение. Приводим матрицу и расширенную матрицу СЛС к каноническому виду.

,

 

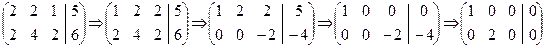
Так как элементарные делители матриц равны, то данная СЛДУ разрешима.

Алгоритм решения СЛС Пусть дана СЛС (2). Запишем ее в матричном виде:

AX º B (mod m), (3)

Расширенную матрицу СЛДУ (2) расширим вторично, приписав к ней снизу единичную матрицу размерности n ´ n и нулевую матрицу размерности n ´1. Получим дважды расширенную матрицу СЛДУ:

.

Преобразуем матрицу A к каноническому виду D, выполняя элементарные целочисленные приведенные преобразования над первыми m строками и первыми столбцами n матрицы . Тогда матрица B перейдет в матрицу F = U ₁ B, где U ₁ - произведение элементарных матриц, соответствующих элементарным преобразованиям строк. Единичная матрица E¢ перейдет в матрицу U ₂, где U ₂ - произведение элементарных матриц, соответствующих элементарным преобразованиям столбцов. Получим матрицу:

.

Полученной матрице соответствует матричное уравнение:

DY º F (mod m), (4)

где Y = U ₂^-1 X, F = U ₁ B, которому соответствует СЛC

(5)

Если хотя бы один из элементов f_{r + 1},…, f_m не сравним с нулем по mod m, или хотя бы одно из чисел f_k не делится на D_k =НОД(d_kk, m), (k =1, 2, …, r), то система (5), а поэтому и система (2) не имеют решений. Если же

D ₁| f ₁,…, D _r | f_r, m | f_{r + 1},…, m | f_m,

то решаем 1-е, 2-е, …, r -е сравнения системы (5) по методу предыдущего параграфа y ₁, y ₂, …, y_r. Значения неизвестных y_{r +1},…, y_n можно брать произвольным образом: y_{r +1}º t ₁, …, y_n º t_{n - r} (mod m). Тогда система (2) имеет D ₁... D _r m^k-r решений по модулю m:

.

Так как Y = U ₂^-1 X, то отсюда находим

X ^{( j )} = U ₂ Y ^{( j )}, (12)

и оно зависит от n - r свободных переменных t ₁, …, t_{n - r} Î Z _m.

Пример 3. Решить СЛC:

Решение. Составим дважды расширенную матрицу и приведем ее к каноническому виду:

 

.

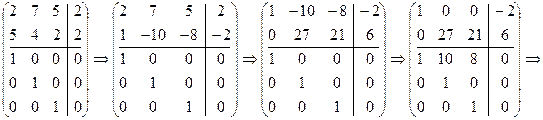
Отсюда приходим к системе сравнений вида (5):

Отсюда

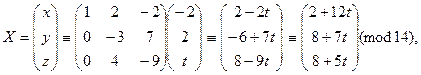
где t Î Z ₁₂. Таким образом, получаем решения сравнения:

.

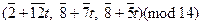Случай, когда дана СЛУ с различными модулями решается более сложно. Рассмотрим СЛС простейшего вида с одним неизвестным:

(6)

но с различными и попарно взаимно простыми модулями.

Теорема 3. Пусть числа m ₁,…, m_k – попарно взаимно простые, числа M ₁,…, M_k и M ₁´,…, M_k ´ определены из условий

m ₁… m_k = M_sm_s, M_s M_s´ º 1 (mod m_s), s = 1,2,…, k, (7)

и пусть

x ₀ = M ₁ M ₁ ´ b ₁ + M ₂ M ₂ ´ b ₂ +…+ M_k M_k´b_k (8)

Тогда совокупность всех значений x, удовлетворяющих системе (5), определяется сравнением

x º x ₀(mod m ₁… m_k). (9)

Доказательство. Для любого j ¹ s все M_j делятся на m_s. Тогда отсюда и из (7) следует, что

x ₀ = M ₁ M ₁ ´ b ₁ + M ₂ M ₂ ´ b ₂ +…+ M_k M_k´b_k º M_s M_s´b_s º b_s (mod m_s), s = 1,2,…, k.

Тогда система (6) равносильна системе:

x º x ₀(mod m ₁),…, x º x ₀(mod m_k). (10)

Так как числа m ₁,…, m_k – попарно взаимно простые, то система (10) равносильна сравнению (9).ÿ

Из теоремы 3 следует, что для любых попарно взаимно простых целых чисел m ₁,…, m_k и любых целых чисел r ₁,…, r_k где 0 £ r ₁ < m ₁,…,0 £ r_k < m_k, существует целое число x, которое при делении на числа m ₁,…, m_k дает соответственно остатки r ₁,…, r_k. Последнее утверждение называется китайской теоремой об остатках. Поэтому и теорему 3 называют китайской теоремой об остатках.

Пример 4. Решить систему сравнение:

Найдем числа M ₁, M₂ и M ₁´, M₂´ из условии (7):

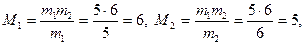
M ₁ M ₁´ º (mod 5), M₂M₂´ º 1 (mod 6),

6 M ₁´ º 1(mod 5), 5 M ₂´ º 1 (mod 6),

M ₁´ º 1(mod 5), M ₂´ º 5 (mod 6),

Тогда число x ₀ вычислим о формуле:

x ₀ = M ₁ M ₁ ´ b ₁ + M ₂ M ₂ ´ b ₂ = 6×1×3 + 5×6×4 = 138 º 18 (mod 30).

Ответ: .

Следствие. Если числа b ₁,…, b_k независимо друг от друга пробегают полные системы вычетов соответственно по модулям m ₁,…, m_k, то число x ₀, определенное по формуле (8) пробегает полную систему вычетов по модулю m ₁… m_k.

Доказательство. Так как числа b ₁,…, b_k независимо друг от друга принимают соответственно m ₁,…, m_k значений, то число x ₀, определенное по формуле (8) принимает m ₁… m_k значений. Покажем, что полученные значения попарно несравнимы по модулю m ₁… m_k Допустим противное, что для двух наборов b ₁,…, b_k, b ₁´,…, b_k´ числа

x ₀ = M ₁ M ₁ ´ b ₁ + M ₂ M ₂ ´ b ₂ +…+ M_k M_k´b_k ,

x ₀´ = M ₁ M ₁ ´ b ₁´ + M ₂ M ₂ ´ b ₂´ +…+ M_k M_k´b_k´

попарно сравнимы по модулю m ₁… m_k. Тогда для любого s = 1, 2, …, k эти числа сравнимы по модулю m_s. Так как для любого j ¹ s все M_j делятся на m_s, то в силу (7) получим

x ₀ º b_s º x ₀´ º b_s´ (mod m_s), для всех s = 1, 2, …, k.

Последнее дает противоречие. Теорема доказана.ÿ

 

6. Сравнения n -й степени по простому и составному модулю

Пусть p – простое число. Пусть f (x) = a ₀ xⁿ + a ₁ x^{n- 1}+…+ a_n Î Z [ x ], a ₀ T 0(mod p). Рассмотрим сравнение

f (x) º 0(mod p). (1)

Так как кольцо классов вычетов Z _p по простому модулю p является полем, то рассматривая сравнение (1) как уравнение над конечным полем Z _p, можем применить к сравнению (1) всю теорию многочленов над конечным полем и получаем следующие теоремы.

Теорема 1. Любое сравнение вида (1) равносильно нулевому сравнению или сравнению степени не большей p- 1.

Доказательство. Разделим многочлен f (x) на многочлен x^p – x с остатком

f (x) = (x^p - x) f ₁(x) + r (x), (2)

где – нулевой многочлен или многочлен степени не выше p- 1. Так как по теореме Ферма для любого целого числа a

a ^p º a (mod m),

то сравнение (1) равносильно сравнению

r (x) º 0(mod p).ÿ

Теорема 2. Число x ₀ удовлетворяет сравнению (1) тогда и только тогда, когда

f (x) º (x - x ₀) f ₁(x)(mod p). (2)

Теорема 3. Если число решений сравнения (1) больше чем n решений, то все его коэффициенты делятся на p.

Доказательство. Допустим, что сравнение (1) имеет, по крайней мере, n + 1 решений. Обозначим числами x ₁, x ₂, …, x_{n +1} вычеты этих решений. Деля многочлен f (x) с остатком последовательно на двучлены x - x ₁, x - x ₂, …, x - x_n представим многочлен f (x) в виде:

f (x) = a ₀(x - x ₁)(x - x ₂)…(x - x_n) + b ₁(x - x ₁)(x - x ₂)…(x - x_{n- 1}) + b_{n- 1}(x - x ₁) + b_n. (3)

Полагая в этом равенстве последовательно x = x ₁, x = x ₂, …, x = x_n, x = x_{n+ 1} получаем

b_n º 0(mod p), b_{n- 1} º 0(mod p), …, b ₁ º 0(mod p), a ₀ º 0(mod p).ÿ

Следствие. Если a ₀ T 0(mod p), то число решений сравнения (1) не больше степени сравнения.

Доказательство. Допустим, что сравнение (1) имеет более чем n решений, то все его коэффициенты делятся на p. Тогда a ₀ º 0(mod p), и получили противоречие с условием.ÿ

Теорема 4 (теорема Вильсона). Число p простое, тогда и только тогда, когда справедливо сравнение

1×2×…(p -1) +1 º 0(mod p) (4).

Доказательство. Длячисла p = 2 сравнение выполняется. Пусть p – нечетное простое число. Тогда по малой теореме Ферма следует, что сравнение

x^{p- 1} º 1(mod p)

имеет p -1 решений `0, `1,…, `p-1. Тогда по теореме 2 получим:

x^{p- 1} -1 º (x - 1)(x - 2)…(x – p + 1) (mod p).

Отсюда при x º 0(mod p) следует формула (4).ÿ

Теорема 5. Пусть m = m ₁… m_k, где числа m ₁,…, m_k попарно взаимно простые. Тогда сравнение

f (x) º (mod m) (5)

равносильно системе сравнений

(6)

при этом, число T решений сравнения (5) равно

T = T ₁… T_k,

где T ₁,…, T_k – обозначают соответственно число отдельных решений сравнений системы (6).

Доказательство. Первая часть теоремы 1 следует из свойства делимости на взаимно простые числа:число a делится на m тогда и только тогда, когда оно делится на каждый из взаимно простых множителей m ₁,…, m_k числа m.

Пусть теперь все попарно различные решения соответственно сравнений системы (6). Тогда для каждого набора чисел ; i= 1,…, T ₁;…; j= 1,…, T_k по формуле (8) предыдущего параграфа находится число, удовлетворяющее всем сравнениям системы (6), т.е. удовлетворяющее системе (5). При этом все полученные числа попарно несравнимы по модулю m. Таким образом система (6) имеет T = T ₁… T_k решений.ÿ

Пусть 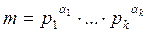- каноническое разложение числа m. В виду теоремы 5 исследование и решение сравнения

(7)

сводится к исследованию и решению сравнений:

. (8)

Поэтому рассмотрим сравнение вида:

, (9)

где p – простое число. Покажем, что решение этого сравнения сводиться к решению сравнения (1).

Теорема 6. Всякое решение x º x ₁ (mod p) сравнения (1) при условии, что f´ (x ₁) не делится на p, даст одно решение сравнения (9):

(10)

Доказательство. Так как всякое число x, удовлетворяющее сравнению (9) удовлетворяет и сравнению (1), то x º x ₁ (mod p), где x ₁ – какое-нибудь решение сравнения (1).

Обратно, пусть x ₁ – любое решение сравнения (1), x º x ₁ (mod p). Тогда x = x ₁ + pt ₁, где t ₁ – целое число. Подставляем это значение x в сравнение

(11)

и применяем формулу Тейлора n -го порядка, получим:

Заметим, что в этой формуле все коэффициенты в формуле целые числа и последние n – 2 членов делятся на p. Тогда сравнение (11) принимает вид:

Так как f´ (x ₁) не делится на p, то последнее сравнение имеет единственное решение

t ₁º t ₁´(mod p), t ₁= t ₁´ + pt ₂,

где t ₂ – целое число. Тогда выражение для x принимает вид

x = x ₁ + pt ₁´ + p ² t ₂ = x ₂ + p ² t ₂,

где t ₂ – целое число. Подставляя это значение x в сравнение

получаем

(12)

Так как x ₂º x ₁(mod p), f´ (x ₂) º f´ (x ₁) (mod p), то f´ (x ₂) не делится на p. Поэтому сравнение (12) имеет одно решение

t ₂º t ₂´(mod p), t ₂= t ₂´ + pt ₃,

где t ₃ – целое число. Тогда выражение для x принимает вид

x = x ₂ + p ² t ₂´ + p ³ t ₃ = x ₃ + p ³ t ₂,

Продолжая эти рассуждения, получим справедливость утверждения теоремы.ÿ

 

Пример 1. Решить сравнение

f (x) = 2 x ³ - x ² + 3 x +2 º 0 (mod 225). (13)

Так как 225 = 3²5², то сравнение равносильно системе сравнений:

(14)

Решаем сравнения

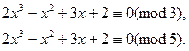
методом испытаний, выполняя проверку по схеме Горнера:

a		-1
		-1			mod 3
					mod 3
					mod 3
		-1			mod 5
					mod 5
					mod 5
					mod 5
					mod 5

Первое сравнение имеет 1 решение x º 1(mod 3), второе сравнение имеет 1 решение x º 2(mod 5). Далее

f´ (x) = 6 x ² - 2 x + 3.

Так как

f´ (1) = 7 º 1 T 0(mod 3),

f´ (2) = 24 – 4 + 3 = 23 º 3 T 0(mod 5),

то каждое из сравнений (14) и сравнение (13) имеет по одному решению.

Решая первое из сравнений (14) положим x = 1 + 3 t ₁, где t ₁ – целое число. Подставляем это значение x в сравнение, получим

Решая второе из сравнений (14) положим x = 2 + 5 t ₁, где t ₁ – целое число. Подставляем это значение x в сравнение, получим

Все решения сравнения (13) являются решениями системы сравнений:

Найдем числа M ₁, M₂ и M ₁´, M₂´ из условии (7):

M ₁ M ₁´ º (mod 9), M₂M₂´ º 1 (mod 25),

25 M ₁´ º 1(mod 9), 9 M ₂´ º 1 (mod 25),

M ₁´ º 4(mod 5),

M ₂´ º 9¹⁹ º 9× (9 ²)⁹ º 9×6× (6 ²)⁴ º 4× (11 ²)² º 4× 4 ² º -4×9 º -11 (mod 25),

Тогда число x ₀ вычислим о формуле:

x ₀ = M ₁ M ₁ ´ b ₁ + M ₂ M ₂ ´ b ₂ = 25×4×4 - 9×11×12 = 112 (mod 225).

Ответ: .