Детерминированные алгоритмы проверки на простоту.

Лекция 6. Криптосистема RSA

План

 

Простые и составные числа. Критерий простоты числа.

Теорема Евклида. Неравенство Чебышева.

Основная теорема арифметики

Алгоритмы генерации простых чисел.

Детерминированный алгоритм проверки на простоту М.Аграваля, Н.Каяля и Н.Саксены.

Вероятностные алгоритмы проверки на простоту.

Криптосистема RSA.

 

1. Простые и составные числа. Критерий простоты числа. Теорема Евклида. Неравенство Чебышева Алгоритмы генерации простых чисел.

Определение 1. Целое число a > 1 называется составным, если его можно представить в виде произведения двух целых чисел, больших единицы, т.е.

a = a ₁ a ₂, (1)

где a ₁ > 1, a ₂ > 1, a ₁ , a ₂ Î Z.

Определение 2. Целое число p > 1 называется простым, если его нельзя представить в виде произведения двух целых чисел, больших единицы, т.е. нельзя представить в виде:

p = a ₁ a ₂, (2)

где a ₁ > 1, a ₂ > 1, a ₁ , a ₂ Î Z.

Теорема 1. Любое целое число a > 1 имеет хотя бы один простой делитель.

Доказательство. Рассмотрим множество M всех делителей числа a, которые больше 1. Множество M не пусто, так как a | a и a > 1. Следовательно, во множестве M есть наименьшее число. Обозначим это число через p и покажем, что p есть простое число. Допустим противное, что число p составное. Тогда его можно представить в виде (2), где a ₁ > 1, a ₂ > 1, a ₁ , a ₂ Î Z. Отсюда a ₁| p. Так как p | a, то a ₁| a и a ₁ = p/a ₂ < p. Получили противоречие. Следовательно, p есть простое число.ÿ

Теорема 2. Целое число a > 1 составное тогда и только тогда, когда оно имеет хотя бы один простой делитель p .

Доказательство. Пусть число a > 1 составное. Тогда для него имеет место представление (1). Покажем, что хотя бы одно из чисел a ₁ или a ₂ . Допустим противное. Тогда оба числа a ₁ и a ₂ . Отсюда

.

Получаем противоречие. Таким образом, хотя бы одно из чисел a ₁ или a ₂ . Допустим для определенности, что a ₁ . Так как число a ₁ > 1, то оно имеет простой делитель p, который является делителем числа a. Так как , то первая часть теоремы доказана.

Обратно, если число a > 1 имеет простой делитель p , то Следовательно, число a составное.ÿ

Теорема 3. Целое число p > 1 простое тогда и только тогда, когда оно не имеет простых делителей p .

Доказательство. Доказательство основывается на теореме 2 ипроводится методом от противного. ÿ

Из теорем 1 и 2 следует метод проверки целого числа на простоту.

Алгоритм проверки числа на простоту.

Ввод: число a.

r:=1 ;d:= 2;

while r ¹0 and d ²£ a do (q, r): = div (a, d); d:= d + 1; end while

if r =0 then s:= «число составное» else s:= «число простое»; end if.

Вывод: s и x (t), y (t).

На теоремах 2 и 3 основан метод нахождения всех простых чисел в заданных пределах, называемый решетом Эротосфена. Например, чтобы найти все простые числа в пределах от 1 до n поступают следующим образом:

1. Выписывают все числа от 1 до n. Первое число этой последовательности 1 непростое и его вычеркиваем.

2. Первое не вычеркнутое число 2, оно простое. Вычеркиваем каждое второе число, считая с 3, т.е. вычеркиваем все числа кратные 2, кроме 2.

3. Первое не вычеркнутое число 3, оно простое. Вычеркиваем в ряде каждое третье число, считая с 4, вычеркнутые числа учитываются, т.е. вычеркиваем все числа кратные 3, кроме 3.

4. Первое не вычеркнутое число 5, оно простое, если бы оно было непростое, то имело простой делитель p и было вычеркнуто на предыдущих шагах. Вычеркиваем в ряде каждое пятое число, считая с 6, вычеркнутые числа учитываются, т.е. вычеркиваем все числа кратные 5, кроме 5.

Продолжаем этот процесс до тех пор пока на некотором шаге не появится первое невычеркнутое число a 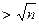. Тогда это число a и все невычеркнутые в ряду числа будут простыми, так как они не имеют простых делителей p .

Пример 1. Найти все простые числа от 1 до 50.

На промежутке от 1 до 50 содержится 15 чисел.

Алгоритм «решето Эротосфена».

Ввод: Число n.

m:=0; r:= b;a 1:= a;;b 1:= b;

{Занесение единиц в массив}

for i:=2… n; a_i: = 1; end for;

p:=2; m:=2;

while p ²£ n do m:= p ²;

{Вычеркивание чисел кратных p }

while m £ n do a_i: = 0; m:= m + p;; end while;

m:= p + 1;

{Нахождение очередного невычеркнутого числа}

while a_m =0 do m:= m + 1; end while;

p:= m

end while;

{Занесение полученных простых чисел в массив P }

т:= 0; for i:=2… n; if a_i: = 1 then m:= m +1; P_m: = i; end if; end for.

Вывод: m и P.

1. Теорема Евклида. Неравенство Чебышева.

 

Теорема 4 (Евклида). Простых чисел бесконечно много.

Доказательство. Доказываем методом от противного. Допустим, что простых чисел конечное число и p ₁, p ₂, …, p_n – список всех простых чисел. Составим натуральное число a = p ₁ p ₂· …· p_n +1. Так как число a > 1, по теореме 1 оно имеет хотя бы один простой делитель p, который совпадает с одним из данных простых чисел. Тогда p | a и p |(p ₁ p ₂· …· p_n). По свойствам делимости получаем p |1 и по свойствам делимости p = ±1. Получаем противоречие с определением простого числа.ÿ

Вопрос, о том как простые числа распределены в натуральном ряду стоял в течении более 2000 тысяч лет и впервые существенные результаты в этом направлении были получены во второй половине 19 века русским математиком П.Л. Чебышевым.

Пусть - число всех простых чисел, не превосходящих x. Функция называется функцией распределения простых чисел. В силу примера 1 получаем

График функции выглядит следующим образом.

Теорема 5 (неравенства Чебышева). Существуют такие два действительных числа a и b, 0 < a <1< b,что выполняется неравенства

.

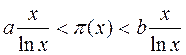П.Л.Чебышев показал, что 0,921 £ a <1< b £ 1,106.

Теорема 5 (Теорема Чебышева, 1848 г.). Если существует предел

, (3)

то он равен (3) существует доказал.

То что предел (3) существует доказали независимо друг от друга Адамар и Валле-Пуссен в 1896 году. Из этого следует, что

.

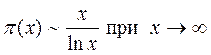В 20 веке было получено много интересных результатов, связанных с поведением функции .

1. Основная теорема арифметики

Теорема 1 (основная теорема арифметики). Любое целое число a > 1 представляется в виде произведения простых чисел:

a =p ₁ p ₂… p_k, (1)

где p ₁, p ₂,…, p_k – простые числа и такое представление единственно с точностью до порядка следования простых сомножителей, т.е. если есть второе представление вида

a =q ₁ q ₂… q_m, (2)

где q ₁, q ₂,…, q_m – простые числа, то k=m и при соответствующей перестановке сомножителей p_i = q_i для всех i = 1, 2,…, k.

Разложить число на множители значит факторизовать число.

Рассмотрим разложение (1) числа a на простые множители. В этом разложении могут оказаться одинаковые простые множители. Произведение всех простых множителей запишем в виде натуральной степени одного простого числа и представим число a в виде:

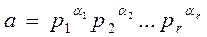, (5)

где - попарно различные простые числа, a₁, a₂,…,a _r - натуральные числа (иногда в этом разложении допускаются и нулевые показатели, когда соответствующий неприводимый многочлен).

Представление целого числа в виде (5) называется каноническим представление целого числа a. В силу теоремы предыдущего параграфа получаем следующую теорему.

Теорема 2. Для любых целого числа a > 1 каноническое разложение (6) существует и оно однозначно с точностью до порядка следования степеней простых чисел.

В теории чисел более двух тысяч лет решались две основные задачи:

1. Задача тестирования целого числа на простоту: найти наиболее быстрый алгоритм определения, является данное целое число a простым или составным.

2. Задача факторизации: нужно разложить число a на множители, если известно, что оно простое.

Оказалось, что эти задачи принципиально отличаются по трудности. Распознать, на простоту наугад взятое число, содержащее 125 и более десятичных знаков можно за несколько минут, а для того чтобы разложить такое число на множители может потребоваться миллионы лет машинного времени.

В связи с появлением в криптографии алгоритмов несимметричного шифрования оказалось, что эти задачи имеют большое практическое значение. Через две тысячи лет теория чисел стала прикладной наукой. В последние два десятилетия интерес к этим задачам теории чисел многократно возрос. Появилось большое число работ, посвященных этим задачам.

Отметим, что задача факторизации более трудная задача чем задача тестирования числа на простоту, на чем и основан алгоритм RSA.

 

1. Алгоритмы генерации простых чисел.

 

Имеется два вида алгоритмов тестирования чисел на простоту:

1) детерминированные алгоритмы, когда строго доказано, что найденное в результате вычислений «простое» число достоверно является простым.

2) Вероятностные алгоритмы, когда найденное в результате вычислений «простое» число с очень большой степенью вероятности является простым. Найденные таким образом числа, простые числа называются псевдопростыми или коммерческими простыми числами

Детерминированные алгоритмы проверки на простоту.

К детерминированным алгоритмам проверки числа на простоту относится, указанный выше классический алгоритм. В связи с криптографическими приложениями простых чисел, интерес к быстрым детерминированным алгоритмам поиска простых чисел усилился.

В последние десятилетия появилось множество различных алгоритмов тестирования и факторизации целых чисел. Найдены быстрые алгоритмы тестирования на простоту целых чисел и новые алгоритмы факторизации, но тем не менее скорость факторизации чисел на десятки порядков ниже скорости их тестирования.

В начале 80-х годов Адлеман, Померанс и Румели предложили детерминированный алгоритм проверки простоты чисел, для заданного натурального числа n алгоритм делает операций. Существенное улучшение их алгоритма в 1981 году получено Х.Ленстрой. Реализация этого алгоритма позволила проверять на простоту числа n порядка 10¹⁰⁰ за несколько минут. В настоящее время удается тестировать на простоту числа порядка 10¹⁰⁰⁰. В 1992 г Адлеман и Хуанг предложили вероятностный алгоритм проверки на простоту чисел, полиномиальной сложности, теоретическая оценка операций. Индийскими математиками Агравала, Кайала и Саксены в 2002 г. получен алгоритм проверки целого числа на простоту полиномиальной сложности, теоретическая оценка операций.

Алгоритм факторизации числа n с помощью пробного деления, опирающийся на теорему 2 предыдущей главы требует арифметических операций. Алгоритм Шермана - Лемена, полученный в 1974 году, требует 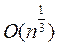арифметических операций. Лучший из детерминированных алгоритмов факторизации Полларда - Штрассена, найденный в 1974 году, требует 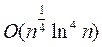арифметических операций для разложение числа на два множителя.

Пусть

.

Существуют алгоритмы факторизации натуральных чисел n, делающие 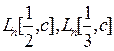арифметических операций. Например, алгоритм квадратичного решета составляет арифметических операций и позволил факторизовать 129-значное RSA-число. Другой алгоритм решета числового поля позволил разложить в 2000 году 155-значное RSA - число – число 512 бит. На факторизацию последнего числа ушло 8400 mips-year (при миллионе операций в секунду 8400 годов).

Указанные алгоритмы имеют сложную теоретическую базу и опираются на свойства гауссовых сумм и характеры Дирихле, алгоритмы имеют сложную структуру.

В августе 2002 года М.Агравалем, Н.Каялем и Н.Саксеной из Индиского технологического института в Капнуре был найден детерминированный полиномиальный алгоритм. Остановимся на сути этого алгоритма, используя замечательную современную монографию Ю.И.Манина и А.А.Панчишкина Введение в современную теорию чисел, 2009, с. 101.

1. Детерминированный алгоритм проверки на простоту М.Аграваля, Н.Каяля и Н.Саксены.

Вход: целое n > 1

Если (n имеет a^b вид, где a, b натуральные и b >1,) выход СОСТАВНОЕ;

r:=2;

пока (r < n) {

если (r простое) {

если (r делит n) выход СОСТАВНОЕ;

найти наибольший простой делитель q для r -1;

есл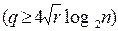и и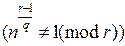

остановка;

}

r:= r +1;

}

для a =1 до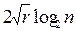

если ()выход СОСТАВНОЕ;

Выход ПРОСТОЕ

Недостаток детерминированных алгоритмов генерации простых больших простых чисел необходимых криптографии, их большая сложность и относительно большое время их генерации. Поэтому в коммерческих приложениях получили распространение так называемые псевдопростые числа, которые находятся вероятностными алгоритмами.

 

1. Вероятностные алгоритмы проверки на простоту.

Вероятностные алгоритмы проверки на простоту основаны на необходимых условиях простоты чисел, таких как теоремы Ферма и Эйлера.

Теорема (теорема Ферма). Для любого простого числа n и для любого целого числом a взаимно простого c n выполняется сравнение

.  (1)

Теорема (теорема Эйлера).). Для любого простого числа n и для любого целого числом a взаимно простого c n выполняется сравнение

.  (2)

В последнем сравнении символ обозначает символ Якоби, который определяется через символ Лежандра. Дадим необходимые определения и свойства, которые позволяют вычислять символы Лежандра и Якоби.

Определение. Пусть p – простое нечетное число, a –целое взаимно простое с p. Число aназывается квадратичным вычетом по mod p, если сравнение

.

разрешимо. Число aназывается квадратичным невычетом по mod p, если это сравнение неразрешимо.

. Символом Лагранжа числа aпо mod p называется символ , читаемый a по p, который равен1, если a - квадратичный вычет поmod p, и равен - 1, если a - квадратичный невычет поmod.

Символ Лежандра можно вычислять по теореме Эйлера, а можно вычислять используя следующие свойства символа Лежандра

1⁰ Если aº b (mod p), то .

2⁰ .

3⁰ Если (ab, p) = 1, то .

4⁰ Если (a, p) = 1, то .

5⁰ Если (ab, p) = 1, то .

6⁰ .

7⁰ (дополнительная теорема к закону взаимности).

8⁰ Если p,q – различные нечетные простые числа, то

(теорема Гаусса, квадратичный закон взаимности).

Для случая составного модуля через символ Лежандра определяется символ Якоби.

Определение. Пусть P – нечетное натуральное число >1, P = p ₁ p ₂×…× p_k – разложение числа P на простые множители. Пусть далее (a, P) = 1. Символ Якоби числа a по P определяется равенством

.

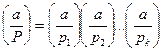Для случая простого нечетного числа P символ Якоби совпадает с символом Лежандра а символ Якоби можно вычислить, используя его свойство, которые доказываются на основе свойств символа Лежандра и аналогичны им:

1⁰⁰ Если aº b (mod P), то .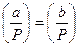

2⁰⁰ .

3⁰⁰ Если (ab, P) = 1, то .

4⁰⁰ Если (a, P) = 1, то .

5⁰⁰ Если (ab, P) = 1, то .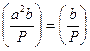

6⁰⁰ .

7⁰⁰ (дополнительная теорема к закону взаимности).

8⁰⁰ Если P,Q – положительные взаимно простые нечетные числа, то

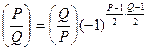(закон взаимности).

Из теорем Эйлера и Ферма следует, что если для нечетное целое n >2 для какого-нибудь целого числа a взаимно простого n либо сравнение (1) либо сравнение (2) не выполняется, то число n будет составным. Если же сравнения (1) и (2) выполняются, то нельзя точно сказать является n простым или составным числом.

Нечетное число n называется псевдопростым числом Ферма по основанию a, (a, n) =1, если выполняется сравнение

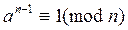.  (1)

Нечетное число n называется псевдопростым числом Эйлера по основанию a, (a, n) =1, если для него если выполняется сравнение

.  (2)

Простые числа являются псевдопростыми по любому основанию a, (a, n) =1.

Вероятностный тест заключается в проверке либо сравнений (1) либо сравнений (2) для нескольких сотен случайно выбранных чисел a, (a, n) =1. Число n, прошедшее такой тест иногда называют «коммерческим» простым числом. Коммерческие простые числа используют в криптографии с открытым ключом, в силу скорости и простоты их нахождения. Вероятность, что таким образом найденное число не является простым очень мала, например, если провели 1000 испытаний, то вероятность равна 2^-1000.

Псевдопростые числа Ферма в настоящее время в криптографии не используются, так как были обнаружены такие составные числа n, которые проходят тест Ферма для любого a, (a, n) =1. Такие числа называются числами Кармайкла l(k). Оказалось, что таких чисел бесконечно много и они могут быть найдены по формуле

,

где

, k имеет каноническое разложение .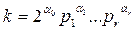

Простота же псевдопростых чисел Евклида может быть выведена из предположения истинности обобщенной гипотезы Римана о нулях L - функций Дирихле. А именно, из этой гипотезы можно вывести, что выполнение сравнений (2) для всех влечет за собой простоту числа n. Для того, чтобы проверить это условие достаточно провести 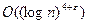делений с остатком для любого выбранного e>0.

Этот алгоритм проверки на простоту называется тестом Соловэй-Стрессена.

Выбираем a случайным образом

Вычислим .

Вычислим символ Якоби

Целое число n псевдопростое по основанию a, если вычисленные числа равны по модулю n.

Предложение. Если n не простое число, и если a случайно выбирается, то вероятность того, что n пройдет тест Соловья-Стрессена меньше чем ½.

Интересный вариант этого теста тест Миллера-Рабина.

Выбираем a случайным образом

Запишем n -1 в виде 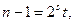где t – нечетное.

Вычислим

.

Целое число n псевдопростое по основанию a, если все числа в указанном выше списке по модулю n равны 1, либо одно из них равно -1.

Более того можно уменьшить вероятность при прохождении теста Миллера-Рабина в 4 раза.

Предложение. Если n не простое число, и если a случайно выбирается, то вероятность того, что n пройдет тест Миллера-Рабина меньше чем ¼.

 

Вероятностный тест проверки на простоту Соловья-Стрссена (не простое с вероятность 1/(2^N))

 

Вход: целые n > 4, N>1

N1:=0;

если (n mod 2 = 0) выход СОСТАВНОЕ

Пока (N1<N){

N1:=N1+1;

a:=2

пока НОД(a, n) > 1{ a:= RND(2, n-2)}

если выход СОСТАВНОЕ

}

Выход ПРОСТОЕ

Вероятностный тест проверки на простоту Миллера-Рабина (не простое с вероятность 1/(4^N))

Вход: целые n > 4, N>1

N1:=0;

если (n mod 2 = 0) выход СОСТАВНОЕ

s:=1;n1:=(n-1)/2;

Пока (n1 mod 2 = 0){n1:=n1/2;s:=s+1;}

Пока (N1<N){

N1:=N1+1; s1:=0;n2:=n1;

a:= RND(2, n-2)}

Пока (s1<s){

если выход СОСТАВНОЕ

m2:=m2*2;s1:=s1+1;

}

Выход ПРОСТОЕ

 

Задание 1: Написать одну из четырех программ (номер программы выбирайте по формуле № =n mod 4 +1, n – номер студента в списке группы

1. Тестирование целого числа на простоту по Эвклиду.
2. Решето Эратосфена.
3. Тестирование целого числа на простоту по Соловью-Стрессену.
4. Тестирование целого числа по Миллеру-Рабину.

Задание 2. С помощью составленной программы составит программу нахождения простого числа, следующего за данными числами 2⁵, 2¹⁰, 2¹⁵,… (интервал между отсчетами подобрать самим, до тех пор пока считает, 10 отсчетов). Составить таблицу найденных простых чисел в виде.

k	2^k	След. прстое	Время вычисления	По Maple программе nextprime

Задание 3. Вычислить количество простых чисел в интервале [ x, L ], x=n*1000, L=x+5000 c (n – номер студента в списке группы) помощью составленной программы или программы Maple, сравнить полученные данные с теоретическими вычисленными по формуле . Найти относительную погрешность.

Задание 4. Оценить относительную и абсолютную погрешность формулы выше для x = n*10, n*50, n*100, n*1000.

Задание 5. Вычислить числа Картмайкла l(k) для числа k = n *100.

Задание 6. Составить программу разложения простого числа на множители. Протестировать программу.

Задание 7. Определить среднюю скорость разложения числа на множители для 10 случайно выбранных чисел из интервала [10*n, 10*n+100000].

 

1. Криптосистема RSA.

В этой части предполагается написать четыре.

1. Генерация ключей RSA.

2. Шифрование RSA.

3. Расшифровывание RSA.

При написании программ используются программы:

1) генерации простых чисел;

2) возведение больших чисел в большую степень по модулю.

3) преобразование текста в целые числа больших систем счисления;

 

Остановимся на основных понятиях криптографии.

Шифрование - преобразовательный процесс: исходный текст, который носит также название открытого текста, заменяется шифрованным текстом (называемый также криптограммой) (рис.1).

Расшифрование - обратный шифрованию процесс. На основе ключа шифрованный текст преобразуется в исходный (рис.2).

Ключ - информация, необходимая для шифрования и дешифрования

текстов.

Криптографическая система представляет собой семейство T преобразований открытого текста. Члены этого семейства индексируются, или обозначаются каким -нибудь символом, например k. Параметр k является ключом.

 

Рис.1. Процесс шифрования данных

 

Рис.2. Процесс дешифрования данных

 

 

 

Пространство ключей K - это набор возможных значений ключа. Обычно ключ представляет собой последовательный ряд букв алфавита. Цель криптографической системы заключается в том, чтобы зашифровать осмысленный исходный текст, получив в результате совершенно бессмысленный на взгляд шифрованный текст. Получатель, которому он предназначен, должен быть способен расшифровать эту шифрограмму, восстановив, таким образом, соответствующий ей открытый текст. При этом противник (называемый также криптоаналитиком) должен быть неспособен раскрыть исходный текст. Существует важное отличие между дешифрованием и раскрытием криптосистемы.

Раскрытием криптосистемы называется результат работы криптоаналитика, приводящий к возможности эффективного раскрытия любого, зашифрованного с помощью данной криптосистемы, открытого текста. Степень неспособности криптосистемы к раскрытию называется ее стойкостью (криптостойкостью), или другими словами криптостойкостью называется характеристика шифра, определяющая его стойкость к дешифрованию без знания ключа (т.е. криптоанализу). Имеется несколько показателей криптостойкости, среди которых:

. количество всех возможных ключей;

. среднее время, необходимое для криптоанализа.

Таким образом, преобразование Tk определяется соответствующим алгоритмом и значением параметра k. Эффективность шифрования с целью защиты информации зависит от сохранения тайны ключа и криптостойкости шифра.

Существуют несколько способов, в соответствии с которыми могут классифицироваться криптографические системы. Например, существует такая классификация:

- криптосистемы ограниченного использования;

- криптосистемы общего использования;

- криптосистемы с секретным ключом;

- криптосистемы с открытым ключом.

Криптографическая система называется криптосистемой ограниченного использования, если ее стойкость основывается на сохранении в секрете самого характера алгоритмов шифрования и дешифрования. Простейшим историческим примером такой системы можно считать шифр Цезаря, который будет рассмотрен далее. Криптосистемы ограниченного использования обычно разрабатываются любителями и почти всегда являются детской забавой для опытного криптоаналитика -профессионала. Гораздо важнее то, что такие системы вообще не используются для конфиденциальной связи в современной ситуации, когда должна обеспечиваться работа большого числа абонентов.

 

В настоящее время получили распространение шифры с открытым ключом. В них для шифрования и для расшифрования применяются разные ключи. Ключ, используемый для шифрования открытый (несекретный), ключ для расшифрования закрытый (секретный и хранится только получателем сообщения). Знания самого сообщения и открытого ключа не достаточно для того, чтобы дешифровать сообщение.

Первой системой с открытым ключом была система RSA.

Криптосистема RSA

Генерация ключей.

Получатель P сообщения производит генерацию открытого ключа (пары чисел n, e) и закрытого ключа (числа d):

1) выбирает два большие простые числа p и q (c сотнями десятичных знаков);

2) определяет первую часть открытого ключа, n = pq;

3) определяет вторую часть открытого ключа, выбирая небольшое нечетное число e, взаимно простое с числом (p -1)(q -1)=j(n);

4) определяет закрытый ключ d, как решение сравнения ed º1(mod (p -1)(q -1)).

5) открытый ключ (числа n, e) сообщаются всем отправителям сообщений.

Шифрование

1.Шифруемое сообщение представляется в виде последовательности слов S ₁, S ₂,… длины log₂ n двоичных разрядов (0≤ S_i < n, i =1.2,…)

2 Каждый блок текста шифруется по правилу:

С_i º S _i ^e (mod n), 0≤ C_i < n, i =1.2,… (1)

и отправляется получателю последовательность чисел С ₁, С ₂,….

Расшифрование.

Зашифрованное сообщение представляется в виде последовательности слов С ₁, С ₂,… (0≤ C_i < n, i =1.2,…) длины log₂ n разрядов.

Оно расшифруется по правилу:

P_i º C _i ^d (mod n). (2)

Получается последовательности слов P ₁, P ₂,… длины log₂ n двоичных разрядов (0≤ P_i < n, i =1.2,…), которая по доказанной ниже теореме совпадает с исходной последовательностью S ₁, S ₂,…, которая преобразуется в исходный текст.

 

.

 

Теорема 1. Шифрование с открытым ключом корректно, т.е. в предыдущих обозначениях P_i=S_i.

Доказательство. Из (1) и (2) получаем P_i º C _i ^d º S _i ^ed (mod n). Покажем, что для любого неотрицательного числа A < n выполняется сравнение A º A ^de (mod n). Так как ed º1(mod (p -1)(q -1)), то ed =1+ k (p -1)(q -1), kÎ Z, и числа e, d взаимно просты с числом (p -1)(q -1).

Если A º0 (mod p), то сравнение A º A ^de (mod p) выполняется. Если A не сравнимо с нулем по модулю p, то по малой теореме Ферма получим

A ^de = A ^{1+ k (p -1)(q -1)} º A × A ^{1+ k (p -1)(q -1)} º A ×(A ^{(p -1)})^{(q -1) k} º A ×(1)^{(q -1) k} º A (mod p).

Аналогично доказываем, что

A ^de º A (mod q).

По определению сравнимости число A ^de - A делится на различные простые числа p,q. Тогда по свойствам делимости число A ^de - A делится на pq=n. Отсюда

A ^de º A (mod n).

Так как P_i º C _i ^d º S _i ^ed (mod n), то P_i º S _i (mod n). По условию 0£ P_i < n, 0£ S _i < n. Тогда P_i = S _i. 

Основой работы системы RSA является сложность задачи факторизации целых чисел, по сравнению с задачей умножения чисел. Большие простые числа p и q просто генерировать, перемножить, найти n = pq. Но очень трудно при заданном n найти множители p и q.

1. Определение простого и составного чисел.

2. Сформулировать критерий простоты числа.

3. Сформулировать теорему Евклида.

4. Дать определение функции распределения простых чисел. Неравенства Чебышева. Закон распределения простых чисел.

5. Основная теорема арифметики.

6. В чем отличие тестов на простоту и тестов факторизации простых чисел.

7. Дать понятие вероятностного и детерминированного тестов проверки числа на простоту.

8. Теорема Ферма и возможность ее использования для тестирования простых чисел на простоту.

9. Псевдопростые числа Ферма.

10. Что такое числа Картмайкла.

11. Что такое квадратичные вычеты и невычеты?

12. Символ Лежандра и его свойства

13. Символ Якоби и его свойства

14. Теорема Эйлера и возможность ее использования для тестирования простых чисел на простоту.

15. Псевдопростые числа Эйлера.

16. Что такое криптосистема? Основные задачи криптографии.

17. Криптографический алгоритм. Криптографический протокол.

18. Принцип Керкгоффса.

19. Что такое ключ шифрования?

20. Что такое открытая и закрытые (асимметричные и симметричные, двухключевые и одноключевые) системы шифрования.

21. Создание ключей в криптосистеме RSA.

22. Шифрование в криптосистеме RSA.

23. Расшифровывание в криптосистеме RSA.

24. Кто такой криптоаналитик? Задачи криптоаналитика.

25. Что такое атака на криптосистему?

26. Что такое активная и пассивные атаки?

27. Стойкость RSA.

28. Уязвимости RSA относительно активных и пассивных атак.