ПАМ
Толстиков А.В.
Практическое занятие 1. Теория делимости целых чисел.
Вопросы для изучения.
1. Делимость целых чисел. Теорема о делении с остатком.
2. Представление целого числа в g-ичной системе счисления.
3. Целочисленная арифметика многократной точности.
4. Наибольший общий делитель целых чисел и наименьшее общее кратное целых чисел. Алгоритм Евклида.
5. Цепные дроби и их свойства. Линейные диофантовы уравнения и их системы.
6. Простые и составные числа. Критерий простоты числа. Теорема Евклида. Неравенства Чебышева.
7. Основная теорема арифметики и следствия из нее.
Задачи для решения на практическом занятии и для самостоятельного решения
1. Перевести число a из системы счисления с основанием g в систему счисления с основанием g 1.
1) a =2345, g = 6, g1 = 16; 2) a = AC345, g = 16, g1 = 8; 3) a = (11,10,21), g = 25, g1 = 10.
2. Выполнить все арифметические операции над данными целыми числами в данной системе счисления.
1) a =(2345)7, b =(53365)7; 2) a =(645B)16, b =(7АD5)16; 3) a =(11,10,21)25, a = (21,15,10)25
3. Вычислить
1) 450; 2) 357; 3) 2100.
4. Найти НОД, НОК и линейное представление НОД целых чисел.
1) a = 345, b = 456; 2) a = 1222, b = 2056; 3) a = 556, b = 782; 4) a = 144, b = 432, c = 330.
5. Разложить данные числа в цепные дроби.
.
6. Решить линейные диофантовы уравнения методом цепных дробей и методом замены переменных.
1) 345 x + 456 y = 12; 2) 124 x - 137 y = 7; 3) 233 x + 25 y = -2; 4) 136 x - 56 y + 14 z = 8.
7. Решить данную систему линейных диофантовых уравнений матричным методом.
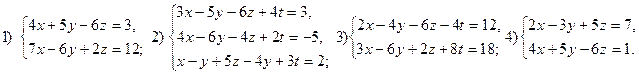
8. Методом решета Эротосфена составить таблицу всех простых чисел от n 1 до n 2 найти значение p(n 2) - p(n 1).
1) n 1 = 100, n 2 = 200; 2) n 1 = 300, n 2 = 400; 3) n 1 = 1000, n 2 = 1100.
9. Вычислить является данное целое a простым или составным.
1) a = 3457; 2) a = 5747; 3) a = 14311; 4) 5371.
10. Факторизовать данные числа.
1) a = 3457; 2) a = 5747; 3) a = 14311; 4) 5371.
Составить программы.
1. Составить программу перевода целых чисел из 10-й системы счисления в систему счисления с основанием машинное слово и обратно.
2. Составить программы реализующие операции целочисленной арифметики многократной точности.
3. Составить программу для вычисления НОД и НОК целых многозначных целых чисел.
4. Составить программу для разложения чисел в цепные дроби.
5. Составить программу для решения линейного диофантова уравнения.
6. Составить программу для решения системы линейных диофантовых уравнений.
7. Составить программу, проверяющее данное многозначное целое число на простоту. Вычисления очередного простого числа из данного интервала. Вычисления значения функции p(x).
8. Составить программу, разлагающее данное многозначное целое число на простые множители.
1. Операции над многозначными целыми числами.
Требуется число a возвести в степень числа m. Представим число m в двоичной системе счисления:
.
Тогда возможны два возможных алгоритма вычисления степени am , которые получаются из следующих равенств:
,
.
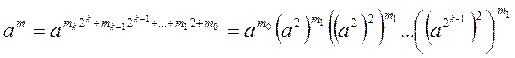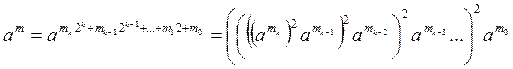Алгоритмы называются бинарными алгоритмами возведения в степень.
НОД. НОК. Алгоритм Евклида.
Теорема 1. Для любых целых чисел a, b ¹ 0 НОД существует, единственен и равен последнему отличному от нуля остатку в алгоритме Евклида, примененного к числам a, b
Пример 1. Найти НОД чисел a = 2346, b = 1456. Применим к данным числам алгоритм Евклида:
2346 = 1456·1+890,
1456 = 890·1 + 566,
890 = 566·1 + 324,
566 = 324·1 + 242,
324 = 242·1 + 82,
242 = 82·2 + 78,
82 = 78·1 + 4,
78 = 4·19 +2,
4 = 2·2.
Таким образом, НОД(a, b) = 2.
Пример 2. Найти линейное представление НОД чисел a = 2346, b = 1456. Используя равенства, полученные в примере 1, получаем:
890 = 2346 - 1456·1 = a - b,
566 = 1456 - 890·1 = b – (a - b) = 2 b - a,
324 = 890 - 566·1 = (a - b) – (2 b - a) = 2 a - 3 b,
242 = 566 - 324·1 = (2 b - a) – (2 a - 3 b) = 5 b - 3 a,
82 = 324 - 242·1 = (2 a - 3 b) – (5 b - 3 a) = 5 a - 8 b,
78 = 242 - 82·2 = (5 b - 3 a) – 2(5 a - 8 b) = 21 b - 13 a,
4 = 82 - 78·1 = (5 a - 8 b) – (21 b - 13 a) = 18 a - 29 b,
2 = 78 - 4·19 = (21 b - 13 a) – 19(18 a - 29 b) = 572 b - 355 a.
Таким образом, НОД(a, b) = 2 = 572 b - 355 a.
Пример 3. Найти НОД чисел a = 2346, b = 1456. Используя вычисления примера 1:
.
Цепные дроби
Определение 1. Непрерывной или цепной дробью называется выражение вида:
Числа a 1, a 2, a 3,… - целые и называются членами цепной дроби; ai > 0, i =2,3,… Если число членов цепной дроби конечно и равно m, то цепная дробь называется конечно цепной дробью длины m, если число членов цепной дроби бесконечное, то дробь называется бесконечной цепной дробью. Цепную дробь обозначают в виде:
[ a 1, a 2, a 3,…, am, …].
Pk / Qk – k -я подходящая дробь к данной цепной дроби.
Пример 4. Представить число a/b, a = 2346, b = 1456 в виде цепной дроби. Применяя вычисления примера 1, получаем:
.
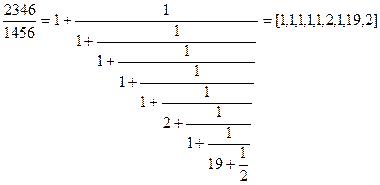Члены цепной дроби разложения действительного числа a последовательно вычисляются по следующему алгоритму:
,
Если a 1 =a, то процесс закончен, если 
.
Если a 2 =a 1, то процесс закончен, если 
.
Таким образом, на k -м мы имеем
Если ak -1 =a k -1, то процесс закончен, если 
.
Пример 5. Представить число 
в виде цепной дроби.
,
,
,
,
.
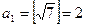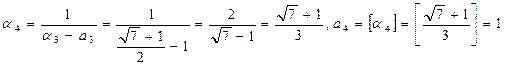Дальше ai и ai начинают повторяться. Поэтому имеем
.
Теорема 2. Числители и знаменатели k-подходящей дроби (k >1) вычисляются по формулам:
Pk = Pk- 1 ak + Pk- 2, Qk = Qk- 1 ak + Qk- 2, (1)
где полагается
P 0 = 1, Q 0 = 0, P 1 = a 1, Q 1 = 1. (2)
Пример 6. Вычислить все числители и знаменатели цепной дроби, полученной в примере 1.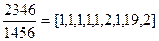 
. Вычисления проводим по формулам (1), (2), записывая результаты вычислений в таблицу.
| k | ||||||||||
| ak | - | |||||||||
| Pk | ||||||||||
| Qk |