Функции случайных величин. Сумма и произведение случайных величин.

Интегральная теорема лапласса.

Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и

единицы, то вероятность 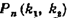того, что событие А появится в п испытаниях от 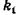до 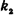раз, приближенно равна определенному интегралу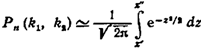

где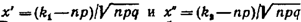

 

10. Дискретные случайные величины (ДСВ). Закон распределения дискретной случайной величины.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Пример – число очков, выпавших на игральной кости.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения ДСВ первая строка таблицы содержит возможные значения, а вторая – их вероятности:

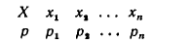
Приняв во внимание, что в одном испытании СВ принимает только одно возможное значение, заключаем, что события X=x₁, X=x₂, X=x_nобразуют полную группу, следовательно, сумма вероятностей этих событий равна единице: p₁ + p₂ + p_n= 1

 

Функции случайных величин. Сумма и произведение случайных величин.

Функция распределения случайной величины X – функция F(x), выражающая для каждогоxвероятность того, что случайная величина X примет значение, меньшее x:

F(x) = P(X<x).

Функцию F(x) называют интегральной функцией распределения или интегральным законом распределения. Геометрически функция распределения интерпретируется, как вероятность того, что случайная точка X попадает левее заданной точки x.

Свойства функции распределения СВ:

1) 0 =<F(x) <= 1;

2) является неубывающей на всей числовой оси;

3)

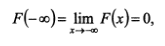
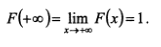
4)P(x₁ =<X<= x₂) = F(x₂) – F(x₁).

Суммой (произведением) случайных величин X и Y называется случайная величина, которая принимает возможные значения видаx_i+y_j(или x_i*y_j) i = 1..n;j=1..m с вероятностями p_ijтого, что случайная величинаX примет значение x_i, а Y–y_j.

p_ij = P[(X=x_i)(Y=y_j)].

!!!!!!12. Математическое ожидание и дисперсия дискретной случайной величины.

Математическим ожиданием ДСВ называют сумму произведений всех её возможных значений на их вероятности.

Пусть случайная величина Xможет принимать только значения x₁, x₂, x_n, вероятности которых соответственно равны p₁, p₂, p_n. Если ДСВ X принимает счётное множество возможных значений, то 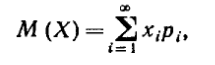, причём математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Вероятностный смысл математического ожидания:

Математическое ожидание приближённо равно среднему арифметическому наблюдаемых значений случайно величины.

Свойства математического ожидания (C - константа):

1) M(C) = C

2) M(CX) = CM(X)

3) M(XY) = M(X)M(Y)

4) M(X+Y) = M(X) + M(Y)

Теорема: Математическое ожидание M(X) числа появлений события A в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: M(X) = np.

Отклонением называют разность между случайной величиной и её математическим ожиданием: X-M(X).

Теорема: Математические ожидание отклонения равно нулю:

M[X-M(X)] = 0.

Дисперсией ДСВ называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

D(X) = M[X-M(X)] ².

Теорема: Дисперсия равна разности между математическим ожиданием квадрата случайной величины X и квадратом её математического ожидания:

D(X) = M(X²) – [M(X)]².

Свойства дисперсии(C - константа):

1) D(C) = 0;

2) D(CX) = C²D(X);

3) D(X + Y) = D(X) + D(Y);

4) D(X - Y) = D(X) + D(Y).

Теорема: Дисперсия числа появлений события A в n независимых испытаниях, в каждом из которых вероятность p появления событий постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X) = npq. (q = 1 - p).

13. Биномиальный закон распределения дискретной случайной величины. Случайная величина может принимать значения 0,1,2,…,n и каждому значению X=m соответствует вероятность 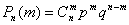, где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появле­нии события в n независимых опытах.

14. Непрерывные случайные величины. Функция распределения и ее свойства.

Случайная величина, значения которой заполняют некоторый промежуток, называется непрерывной.

В частных случаях это может быть не один промежуток, а объединение нескольких промежутков. Промежутки могут быть конечными, полу бесконечными или бесконечными.

Пусть x – непрерывная случайная величина. Функция F (x), которая определяется равенством

,

называется интегральной функцией распределения или просто функцией распределения случайной величины x. Непосредственно из определения следует равенство 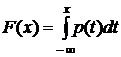. Формула производной определённого интеграла по верхнему пределу в данном случае приводит к соотношению 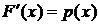. Плотность распределения р (х) называют дифференциальной функцией распределения.

Функция распределения F (x) случайной величины xимеет следующие свойства.

1. F (x) — непрерывная возрастающая функция.

2. ;

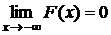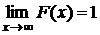
Свойства 1 и 2 вытекают непосредственно из определения функции F (x).

3. Приращение F (x) на промежутке (х ₁; х ₂) равно вероятности того, что случайная величина x принимает значение из этого промежутка:

F (x ₂) – F (x ₁) = P (x ₁ <x£ x ₂)

15.Плотность распределения непрерывной случайной величины ее свойства.

(1)

Функция р (х) называется плотностью распределения случайной величины. Из формулы (1) следует равенство, справедливое для малых величин D х, которое также можно считать определением функции р (х):

P (х < x < х + D х) 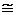p (x)D х (2)

Очевидно, что p (x) – неотрицательная функция. Для определения вероятности того, что случайная величина x примет значение из промежутка [ a, b ] конечной длины, нужно выбрать на промежутке произвольные числа x ₁, х ₂,¼, х_n удовлетворяющие условию а=х ₀< х ₁< x ₂<¼< x_n < b=x_{n+ 1}. Эти числа разобьют промежуток [ a, b ] на n +1 частей, представляющих собой промежутки [ х ₀, х ₁), [ х ₁, х ₂), ¼,[ х_n, b ]. Введём обозначения:

D х ₀= х ₁ – х ₀, D х ₁= х ₂ – х ₁, ¼, D х_n = b – х_n,

и составим сумму . Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что максимальная величина D х_i стремится к нулю. Будем считать функцию p (x) непрерывной на промежутке (а; b), тогда пределом суммы будет определённый интеграл по промежутку [ a; b ] от функции p (x), равный искомой вероятности:

P (a £ x £ b) = 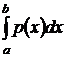(3)

Рис. 1

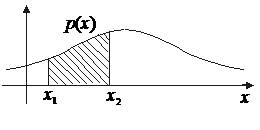Это равенство можно также рассматривать как определение функции р (х). Отсюда следует, что вероятность попадания случайной величины в любой интервал (х ₁, х ₂) равна площади фигуры, образованной отрезком [ х ₁, х ₂] оси х,графиком функции р (х) и вертикальными прямыми х = х ₁, х = х ₂, как изображено на рисунке 1.

Если все возможные значения случайной величины принадлежат интервалу (а; b), то для р (х) – её плотности распре­деления справедливо равенство

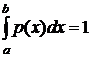
Для удобства иногда считают функцию р (х) определённой для всех значений х, полагая её равной нулю в тех точках х, которые не являются возможными значениями этой случайной величины.

Плотностью распределения может служить любая интегрируемая функция р (х), удовлетворяющая двум условиям:

1) р (х) ³ 0;

2)

 

16.Математическое ожидание и дисперсия непрерывной случайной величины.

Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx.

Математическое ожидание дискретной случайной величины x, имеющей распределение

 

x1 x2... xn

p1 p2... pn

называется величина 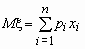, если число значений случайной величины конечно.

Если число значений случайной величины счетно, то . При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

 

Математическое ожидание непрерывной случайной величины с плотностью вероятностей px (x) вычисляется по формуле . При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Если случайная величина h является функцией случайной величины x, h = f(x), то .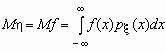

Аналогичные формулы справедливы для функций дискретной случайной величины: .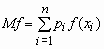

Основные свойства математического ожидания:

· математическое ожидание константы равно этой константе, Mc=c;

· математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин x, h и произвольных постоянных a и b справедливо: M(ax + bh) = a M(x)+ b M(h);

· математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(x h) = M(x)M(h).

Дисперсия случайной величины

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

 

Если случайная величина x имеет математическое ожидание Mx, то дисперсией случайной величины x называется величина Dx = M(x - Mx)2.

 

Легко показать, что Dx = M(x - Mx)2= Mx 2 - M(x)2.

 

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx 2 >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам .

Для определения меры разброса значений случайной величины часто используется среднеквадратичное отклонение, связанное с дисперсией соотношением .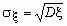

Основные свойства дисперсии:

· дисперсия любой случайной величины неотрицательна, Dx 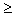0;

· дисперсия константы равна нулю, Dc=0;

· для произвольной константы D(cx) = c2D(x);

· дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(x ± h) = D(x) + D (h).

17.Равномерное распределение непрерывной случайной величины. Непрерывная величина Х распределена равномерно на интервале (a, b), если все ее возможные значения находятся на этом интервале и плотность распределения вероятностей постоянна:

(29)

Для случайной величины Х, равномерно распределенной в интервале (a, b) (рис. 4), вероятность попадания в любой интервал (x1, x2), лежащий внутри интервала (a, b), равна:

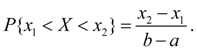(30)

Рис. 4. График плотности равномерного распределения

Примерами равномерно распределенных величин являются ошибки округления. Так, если все табличные значения некоторой функции округлены до одного и того же разряда 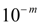, то выбирая наугад табличное значение, мы считаем, что ошибка округления выбранного числа есть случайная величина, равномерно распределенная в интервале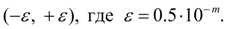

18.Показательное распределениенепрерывной случайной величины. Непрерывная случайная величина Х имеет показательное распределение, если плотность распределения ее вероятностей выражается формулой:

(31)

График плотности распределения вероятностей (31) представлен на рис. 5.

Рис. 5. График плотности показательного распределения

Время Т безотказной работы компьютерной системы есть случайная величина, имеющая показательное распределение с параметром λ, физический смысл которого – среднее число отказов в единицу времени, не считая простоев системы для ремонта.

 

 

19. Нормальное распределениеслучайной величины. Вероятностный смысл параметров нормального распределения.

Нормальное распределение, также называемое гауссовым распределением или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения: где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия. Нормальный закон распределения является предельным законом, к которому приближаются другие законы распределения при часто встречающихся аналогичных условиях.Нормальное распределение играет важнейшую роль во многих областях знаний, особенно в статистической физике. Физическая величина, подверженная влиянию значительного числа независимых факторов, способных вносить с равной погрешностью положительные и отрицательные отклонения, вне зависимости от природы этих случайных факторов, часто подчиняется нормальному распределению, поэтому из всех распределений в природе чаще всего встречается нормальное (отсюда и произошло одно из названий этого распределения вероятностей). Нормальное распределение зависит от двух параметров — смещения и масштаба. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:

отклонение при стрельбе/некоторые погрешности измерений / рост живых организмов

Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный).

Центральная предельная теорема показывает, что в случае, когда результат измерения (наблюдения) складывается под действием многих независимых причин, причем каждая из них вносит лишь малый вклад, а совокупный итог определяется аддитивно, т.е. путем сложения, то распределение результата измерения (наблюдения) близко к нормальному.

 

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

//Про «вероятностный смысл параметров распределения» ничего не смог найти, если у кого-нибудь есть материал по этому вопросу, то дополните п.

20. Свойства нормального распределения. Вероятность попадания нормально распределенной случайной величины в заданный интервал.

Свойство 1: Для любого справедливо соотношение: 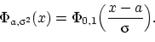Мы сделали замену переменных, 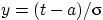, верхняя граница интегрирования при такой замене перешла в

Следствие 1.1. Если 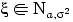, то .

Следствие 1.2. Если 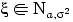, то

Свойство 2. , .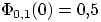

Свойство 3. Если , то для любого

Доказательство. При имеем:

Свойство 4 (правило трех сигм). Если 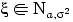, то

Доказательство. Перейдём к противоположному событию: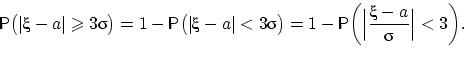

Но величина 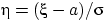имеет стандартное нормальное распределение, и можно использовать свойство 3: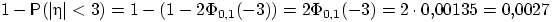

полезно помнить, что почти вся масса нормального распределения сосредоточена в границах от до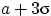

Вероястность попадания сл. величины в заданный интервал вычисляется как разность функций лапласа: Р(а<x<b)=F((b-m)/(дисперсия)^0.5)-F((a-m)/(дисперсия)^0.5)

F-функция Лапласа.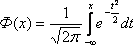

Пример. Случайная величина Х имеет нормальное распределение с параметрами а = 3, σ = 2. Найти вероятность того, что она примет значение из интервала (4, 8).

Решение.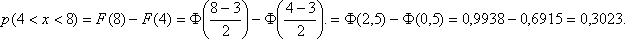

 

21. Нера́венство Чебышева

известное также как неравенство Биенэме — Чебышева, это распространённое неравенство из теории меры и теории вероятностей. Неравенство Чебышева в теории вероятностей утверждает, что случайная величина в основном принимает значения, близкие к своему среднему. Говоря более точно, оно даёт оценку вероятности, что случайная величина примет значение, далёкое от своего среднего. Неравенство Чебышева является следствием неравенства Маркова.

Пусть случайная величина 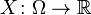определена на вероятностном пространстве 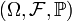, а её математическое ожидание и дисперсия конечны. Тогда

где 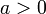. Если 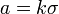, где — стандартное отклонение и 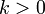, то получаем В частности, случайная величина с конечной дисперсией отклоняется от среднего больше, чем на 2 стандартных отклонения, с вероятностью меньше 25%. Она отклоняется от среднего на 3 стандартных отклонения с вероятностью меньше 11.2%.

22. Закон больших чисел(теорема Чебышева).

 

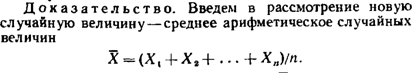
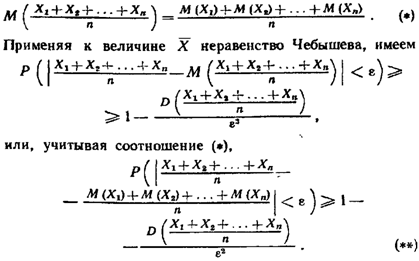
23.Следствия теоремы Чебышева. Закон больших чисел в форуме Бернулли.

 

 

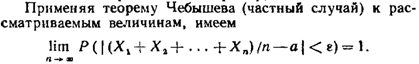
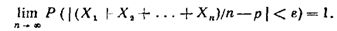
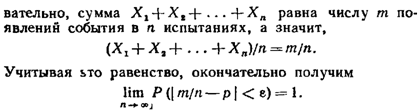
24.Основные понятия математической статистики. Генеральная и выборочная совокупности. Полигон. Гистограмма.

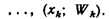
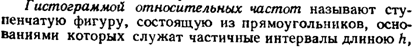
25.Выборочная средняя и выборочная дисперсия.

26.Точечные оценки параметров распределения. Метод моментов для получения точечных оценок.

27. Интервальные оценки параметров распределения.

 

28.Выборочное линейное уравнения регрессии. Нахождение параметров уравнения регрессии методом наименьших квадратов.

Если уравнение регрессии 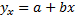, то оценить параметры a и b.

На практике ищут зависимости:

)

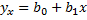
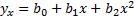
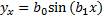
Основным методом является метод наим. квадратов:

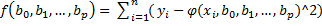, где х,у – элементы выборки

Все частные производные равны 0. Получим р+1 ур-ние с р+1 неизвестным.

29. Нелинейные уравнения регрессии.

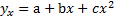
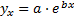* и т.д.

a,b,cнаходятся методом наим. квадратов.

Если уравнение нелинейной регрессии даёт заметную ошибку, то выбираем уравнение, содержащее более высокую степень величины х и останавливаемся на том, которая обеспечивает допустимую погрешность.

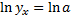+bx

 

 

31.Выборочный коэффициент корреляции

Выборочный коэффициент корреляции определяется равенством

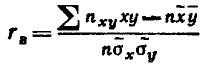
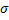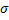где х, у - наблюдавшиеся значения признаков X и Y; nху - частота пары значений (х, у); n - объем выборки; х, у—выборочные средние

квадратические отклонения; х, у—выборочные средние.

Известно, что если величины Y и X независимы, то коэффициент корреляции г=0; если r= 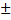1,то Y и X связаны линейной функциональной зависимостью. Отсюда следует, что коэффициент корреляции r измеряет силу тесноту линейной связи между Y и X.

Выборочный коэффициент корреляции rв является оценкой коэффициента корреляции r генеральной совокупности и поэтому также служит для измерения линейной связи между величинами—количественными признаками У и X. Допустим, что выборочный коэффициент корреляции, найденный по выборке, оказался отличным от нуля. Так как выборка отобрана случайно, то отсюда еще нельзя заключить, что коэффициент корреляции генеральной совокупности также отличен от нуля. Возникает необходимость проверить гипотезу о значимости (существенности) выборочного коэффициента корреляции (или, что то же, о равенстве нулю коэффициента корреляции генеральной совокупности). Если гипотеза о равенстве нулю генерального коэффициента корреляции будет отвергнута, то выборочный коэффициент корреляции значим, а величины X и Y коррелированы; если гипотеза принята, то выборочный коэффициент корреляции незначим, а величины X и У не коррелированы.

Если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность (репрезентативна), то заключение о тесноте линейной зависимости между признаками, полученное по данным выборки, в известной степени может быть распространено и на генеральную совокупность. Например, для оценки коэффициента корреляции rг нормально распределенной генеральной совокупности (при n 50) можно воспользоваться формулой

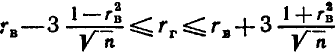
Замечание 1. Знак выборочного коэффициента корреляции совпадает со знаком выборочных коэффициентов регрессии.

Замечание 2. Выборочный коэффициент корреляции равен среднему геометрическому выборочных коэффициентов регрессии.