Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Дано: 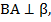
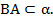
Доказать: 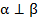
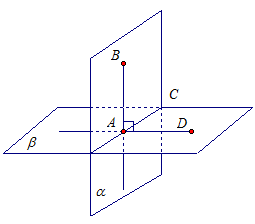
Рис. 3
Доказательство:
Пусть плоскости α и β пересекаются по прямой АС (рис. 3). Чтобы доказать, что плоскости взаимно перпендикулярны, нужно построить линейный угол между ними и показать, что этот угол равен 90°.
Прямая АВ перпендикулярна по условию плоскости β, а значит, и прямой АС, лежащей в плоскости β.
Проведем прямую АD перпендикулярно прямой АС в плоскости β. Тогда ВАD –линейный угол двугранного угла.
Прямая АВ перпендикулярна плоскости β, а значит, и прямой АD, лежащей в плоскости β. Значит, линейный угол ВАD равен 90°. Значит, плоскости α и β перпендикулярны, что и требовалось доказать.
Следствие
Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей (рис. 4).
Дано: 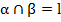
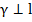
Доказать: 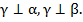

Рис. 4
Доказательство:
Прямая l перпендикулярна плоскости γ, а плоскость α проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости α и γ перпендикулярны.
Прямая l перпендикулярна плоскости γ, а плоскость β проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости β и γ перпендикулярны.
Следствие доказано.
Следствие 2
Плоскость линейного угла перпендикулярна всем элементам соответствующего двугранного угла: ребру и граням.
Дано: 
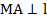 ,
,
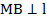 ,
,
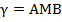 .
.
Доказать:
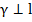 ,
,
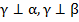 .
.
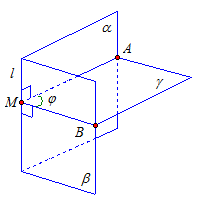
Рис. 5
Доказательство:
Мы имеем двугранный угол, образованный полуплоскостями α и β, которые пересекаются по прямой l (l – ребро двугранного угла) (рис. 5).
На ребре l взята точка М, к ребру l проведены два перпендикуляра МА и МВ в плоскостях α и β соответственно. Пусть пересекающиеся прямые МА и МВ образуют плоскость γ. Это и есть плоскость линейного угла.
Прямая l перпендикулярна двум пересекающимся прямым АМ и МВ из плоскости γ по построению. Значит, прямая l перпендикулярна плоскости γ.
Плоскость α проходит через прямую l, которая перпендикулярна γ, значит, 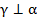 .
.
Аналогично, плоскость β проходит через прямую l, которая перпендикулярна γ, значит, 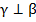 .
.
Итак, доказано, что плоскость линейного угла перпендикулярна всем его элементам: и ребру, и граням.
Утверждение
Если в одной из перпендикулярных плоскостей проведена прямая перпендикулярно к их линии пересечения, то эта прямая перпендикулярна и к другой плоскости.
Дано: 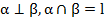 ,
,
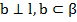 .
.
Доказать: 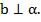
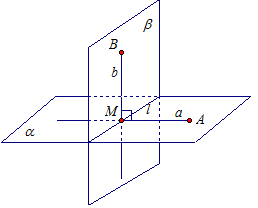
Рис. 6
Доказательство:
Пусть в плоскости β проведена прямая b = MB, которая перпендикулярна к линии пересечения плоскостей – l. (рис. 6)
Проведем прямую МА = а перпендикулярно прямой l. Тогда из точки М проведены два перпендикуляра к ребру l в плоскостях α и β. Получаем ∠АМВ – линейный угол двугранного угла. Так как плоскости α и β перпендикулярны, то ∠АМВ = 90°. Значит, прямые а и b перпендикулярны.
Тогда прямая b перпендикулярна двум пересекающимся прямым а и l из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая b перпендикулярна плоскости α, что и требовалось доказать.
Напоминание определения и признака перпендикулярности прямой и плоскости
Определение. Прямая а называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой из плоскости.
Признак. Если прямая а перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к самой плоскости, а значит, к любой прямой, лежащей в этой плоскости (рис. 7).
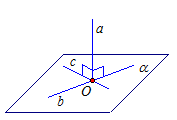
Рис. 7