Пример 13.1. Найдем перемещения для балки, загруженной нагрузкой, интенсивность которой изменяется по закону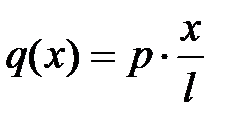 
(рис.13.2,а).
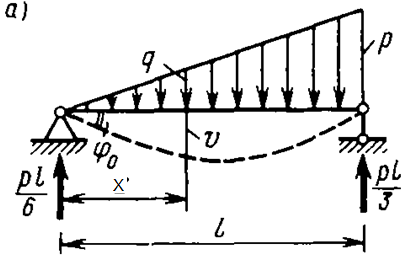
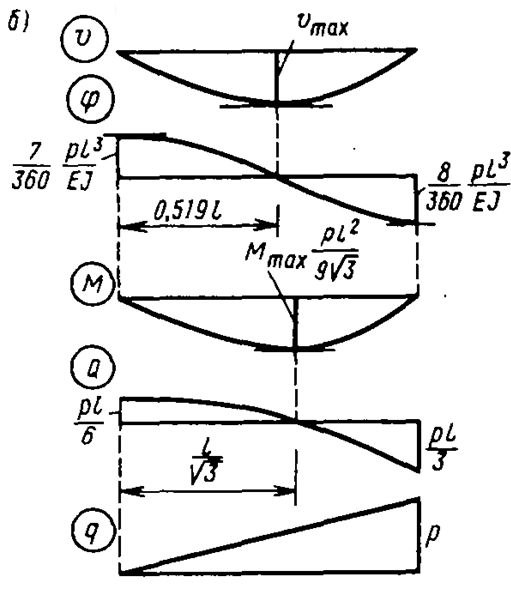
Рис. 13.2 Изгиб шарнирно опертой балки треугольной нагрузкой
Для шарнирно опертой балки (рис. 13.3) воспользуемся дифференциальным уравнением (13.3) и условиями закрепления
Рис. 13.3
  ,
|  .
|
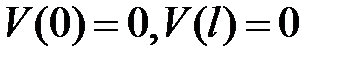Определяем опорные реакции:
 ,
|  ,
|  ,
|
 ,
|  ,
|  .
|
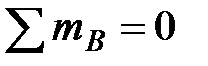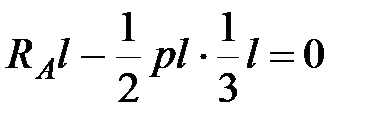В сечении с координатой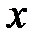 
выражение для изгибающего момента имеет вид:
 ,
|  .
| (13.8) |
Подставляем (13.8) в уравнение (13.3) и интегрируем:
|  
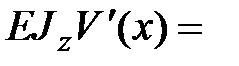
| (13.9) |
 .
| (13.10) |
Вновь интегрируем обе части уравнения (13.10), получаем:
 
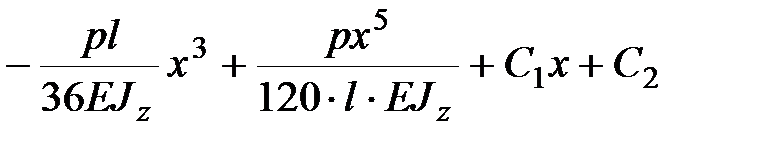
| (13.11) |
Постоянные интегрирования находим из условий закрепления:
Прогиб на левой опоре равен нулю: 
, 
.
Прогиб на правой опоре равен нулю:
, 
, 
.
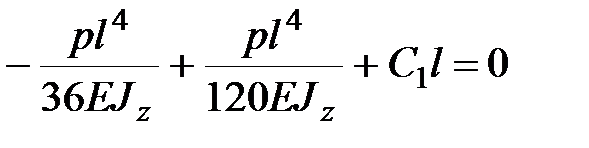Окончательные выражения для искомых функций имеют вид:
 ,
 +  ,
 ,
  ,
 .
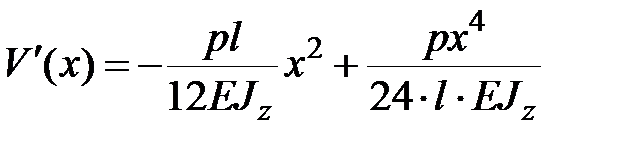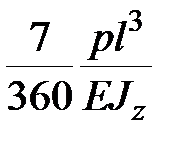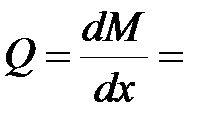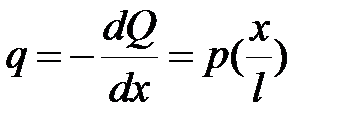| (1.12) |
Эпюры перемещений, усилий и интенсивности нагрузки показаны на рис. 13.2, б. На эпюрах отмечены точки максимума прогибов и изгибающих моментов.
Пример 13.2 Определить прогибы и внутренние усилия M и Q для статически неопределимой балки (рис.13.4)
В этой балке четыре неизвестных реакции (момент и три силы) и только три уравнения для их определения. Поэтому данная задача относится к статически неопределимым.
Для решения данной задачи воспользуемся системой четырех дифференциальных уравнений
 ,
 ,
 ,
 .
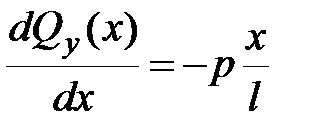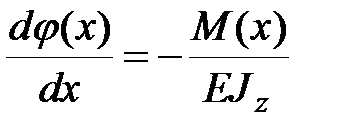| (13.13) |
Интегрирование системы (13.3) выполним с учетом условий закрепления:
 .
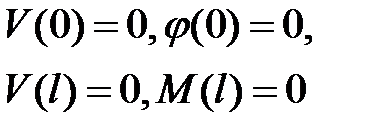| (13.14) |
Интегрируем первое уравнение системы:
| (13.15) |
Подставляем (13.15) во второе уравнение системы и интегрируем:
| (13.16) |
Подставляем (13.16) в третье уравнение системы и интегрируем:
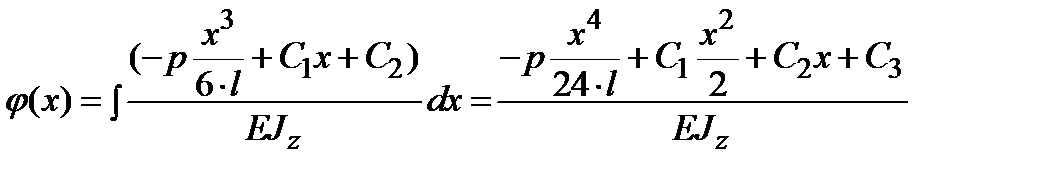
| (13.17) |
Подставляем (13.17) в четвертое уравнение системы и интегрируем:
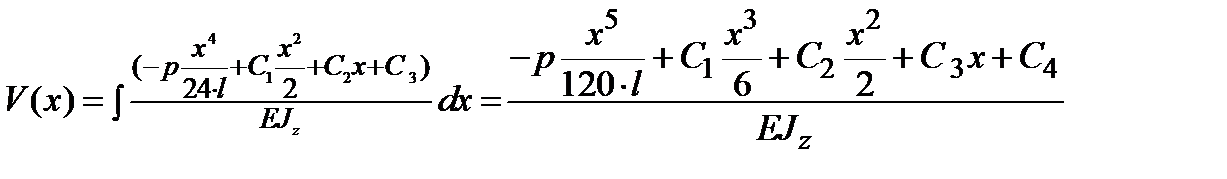
| (13.18) |
Постоянные интегрирования определяем из условий закрепления:
1) 
, из (13.17) получим 
.
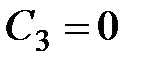2) 
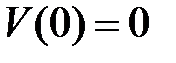, из (13.18) получим 
.
3) 
, из (13.16) получим: 
4) 
, из (13.18) получим: 
.
Из условий 1-го и 2-го условий вытекает геометрический смысл постоянных интегрирования.
Константа 
пропорциональна прогибу в начале координат, а константа 
углу поворота сечения в начале координат.
Решаем систему уравнений (3-е и 4-е условия):
Рис. 13.4 Эпюры прогибов, изгибающих моментов и поперечных сил в статически неопределимой балке
 ,
,
| (13.19) |
Умножаем первое уравнение на 
и вычитаем из второго, получаем
| (13.20) |
Подстановка констант в уравнения (13.15)-(13.18) дает
| (13.21) |
Эпюры перемещений и усилий представлены на рис.13.4.
Использование локальной системы координат при наличии нескольких участков интегрирования.
Пример 13.3
a = 3.9м, b = 0.9м, c = 1.2м, 
кН/м, 
кН/м,
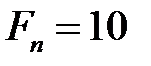кН,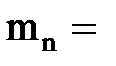 
5кН×м, 
;
сталь: 
МПа, 
ГПа, 
;
древесина: 
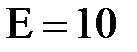МПа, 
ГПа, 
.
Расчетные нагрузки:
кН/м, 
кН/м, 
кН,
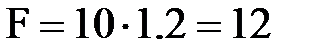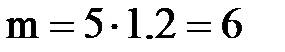кН×м.
Расчетная схема балки приведена на рис. 13.5
Рис.13.5 Расчетная схема балки
Выражения для изгибающих моментов на участках имеют вид (см. лекцию №12 пример 12.1):
 ,  ,
 .
| ( )
|
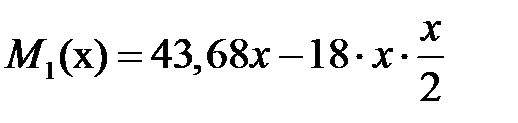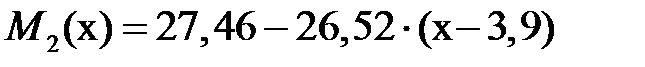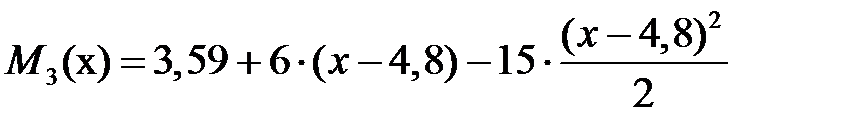Записываем дифференциальное уравнение оси изогнутой балки на первом участке и дважды его интегрируем
Первый участок 
 ,
 ,
|
( )
( )
( )
|
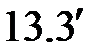Записываем дифференциальное уравнение оси изогнутой балки на втором участке и дважды его интегрируем
Второй участок 
 ,
 ,
 .
| ( )
( )
( )
|
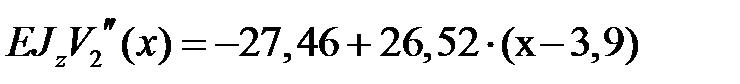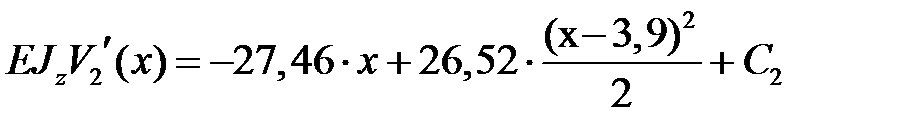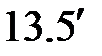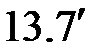Записываем дифференциальное уравнение оси изогнутой балки на третьем участке и дважды его интегрируем
Третий участок 
 ,
 ,
 .
|
( )
( )
( )
|
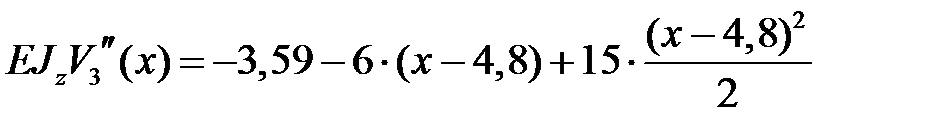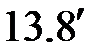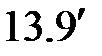Константы интегрирования определим из условий закрепления балки и условий непрерывности функции прогиба и ее производной на границах участков.
На левом конце балка опирается на опору, прогиб в точке равен нулю 
, следовательно
 .
| ( )
|
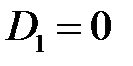Условия сопряжения на границе 1-го и 2-го участков имеют вид: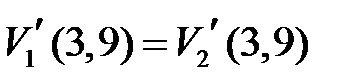 
, 
. С учетом выражений (
) и (
) получим
 .
|
( )
|
С учетом выражений (
) и (
) будем иметь
 .
|
( )
|
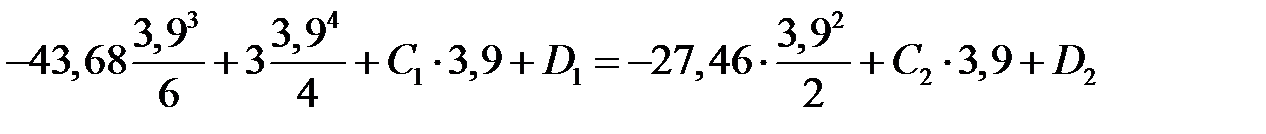Условия сопряжения на границе 2-го и 3-го участков имеют вид: 
, 
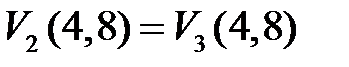. С учетом выражений (
) и (
) получим
|
( )
|
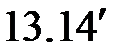С учетом выражений () и (
) будем иметь
 .
|
( )
|
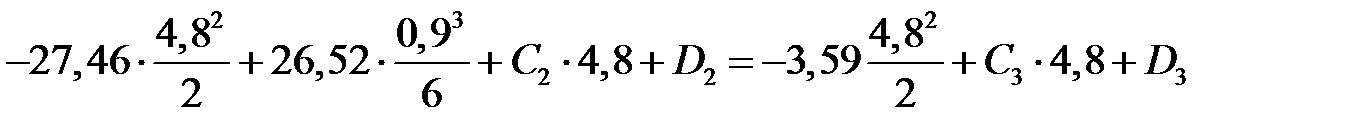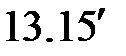В точке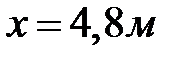 
балка опирается на опору, прогиб в точке равен нулю 
|
( )
|
Уравнения (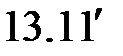
)-(
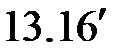) образуют систему линейных алгебраических уравнений, которая имеет вид:
 ,
 ,
 ,
 ,
|
( )
|
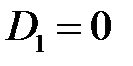
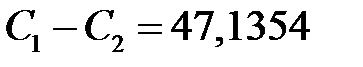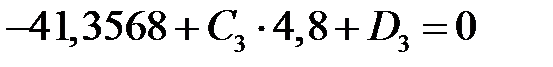
Система уравнений (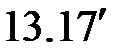
) легко разрешима. Действительно, из 1-го и 2-го уравнений имеем: 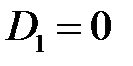, , 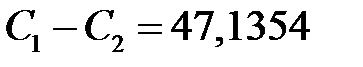тогда из 3-го уравнения находим 
. Используем 4-е уравнение 
, тогда с учетом из 5-го получаем 
. Подставляем 
в 6-е уравнение, находим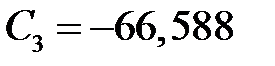 
. Из 4-го определяем 
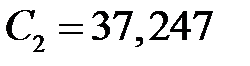. Из 2-го уравнения находим 
.
Результат решения системы: ; ; ; ; ; .
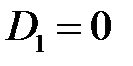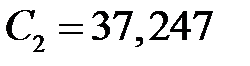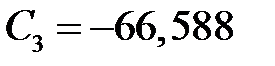Подставляем значения констант интегрирования в выражения для прогибов и углов поворота, получаем:
,
,
,
,
,
.
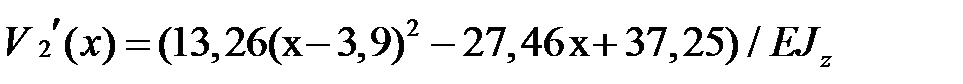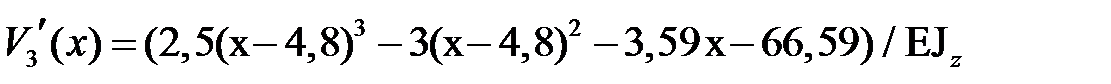При решении задачи использованы выражения для изгибающих моментов, полученные от действия расчетной нагрузки. Прогибы и углы поворота сечений балки определяются от действия нормативной нагрузки. Поэтому при вычислении перемещений их численные значения необходимо разделить на коэффициент надежности по нагрузке .
Прогиб в середине пролета балки от нормативной нагрузки
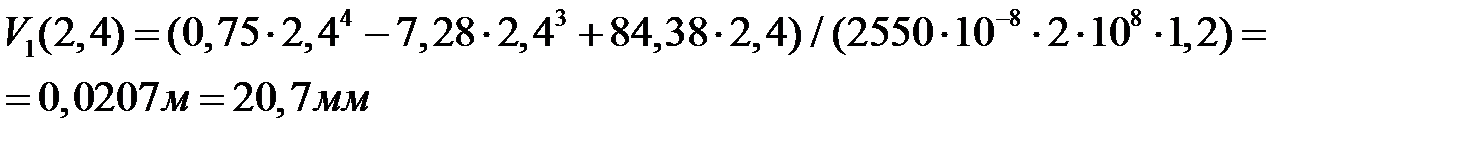
Прогиб на конце консоли от нормативной нагрузки 
Угол поворота сечения на левой опоре от нормативной нагрузки 
. Угол поворота сечения на правой опоре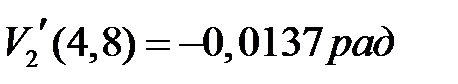 
.
Эпюры углов поворота сечений и прогибов представлены на рис. 13.6, 13.7.
Рис. 13. 6 Углы поворота сечений
| 
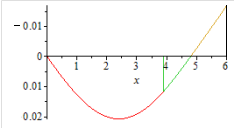Рис. 13.7 Прогибы
|
Точка, в которой 
, определяется из решения кубического уравнения
.
Корни кубического уравнения: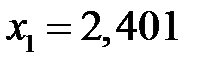 
; 
; 
. Подходит только корень 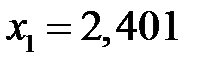. Значение функции прогибов в точке экстремум 
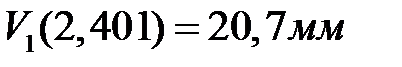(вычислено раннее).
Данное исследование необходимо, если требуется проверить условие жесткости, когда величина допустимого прогиба задана.