Переключательные функции. Графы
Для заочников специальности 2204
Часть I. Переключательные функции
Переключательные или логические функции находят широкое применение при разработке современной вычислительной техники и ее применении. Они осуществляют однозначное отображение множества наборов 
, в которых переменные 
принимают значения из множества 
в множество 
. Чаще всего рассматривают переключательные функции для к=2. Множество в этом случае или просто 
состоит всего из двух элементов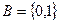 
. Такие переключательные функции называют еще булевыми функциями, а переменные, принимающие значения из , — булевыми переменными.
Любую булеву функцию можно задать с помощью таблицы, в которой перечисляются все наборы значений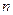 
переменных, т.е. двоичные 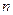-мерные векторы 
…, 
и соответствующие им значения функции. Всего таких наборов будет 
. Располагаются они, как правило, в порядке возрастания соответствующих им двоичных чисел. При таком упорядочении функция полностью определяется -мерным двоичным вектором. Всего таких векторов будет 
, значит и различных булевых функций от 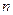переменных будет .
Примеры логических функций.
Таблица функций одной переменной
| 0 1 | Обозначение (формула) | Название |
| 0 0 | Константа 0 | |
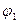
| 0 1 |
| Переменная х |
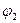
| 1 0 |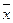 
| Отрицание |
| 1 1 | Константа 1 |
Таблица функций от двух переменных
| Обозначение | Название | ||||
| Константа 0 | |||||
| 
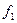
| Конъюнкция | ||||
| 
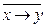
| Отрицание импликации | ||||
|
| Переменная х (y – фиктивная переменная) | ||||
| 
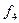
| Отрицание обратной импликации | ||||
|
| Переменная y (х – фиктивная переменная) | ||||
|
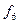
| Сложение по модулю 2 (неравнозначность, исключённое или) | ||||
| 
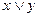
| Дизъюнкция | ||||
| 
| Стрелка Пирса (отрицание дизъюнкции, конъюнкция отрицаний, функция Даггера) | ||||
| 
| Эквиваленция (равнозначность) | ||||
| 
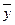
| Отрицание y | ||||
| 
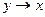
| Обратная импликация | ||||
|
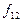
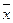
| Отрицание х | ||||
| 
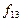
| Импликация | ||||
| 
| Штрих Шеффера (дизъюнкция отрицаний, отрицание, конъюнкции) | ||||
| Константа 1 |
Таким образом, логические функции можно задавать таблицей (таблицей истинности), вектором (оставив от таблицы последний столбец) или формулой.
В каждую функцию вместо любой из переменных можно подставить другую функцию, получается так называемая суперпозиция функций.
Пример. Пусть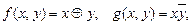 
тогда
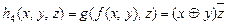
и т.д. — различные суперпозиции функци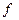й 
и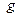 
.
Разные формулы могут задавать одну и ту же функцию. Такие формулы называются равносильными (соединяются обычным знаком равенства). Доказать равносильность формул можно с помощью таблиц истинности.
Пример. Проверить, являются ли равносильными формулы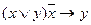 
и 
.
Решение. Составим таблицы истинности для этих формул, совместив их.
|
|
| 
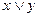
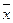
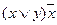
| Первая формула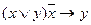
|
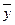
| Вторая формула
|
| 0 0 | ||||||
| 0 1 | ||||||
| 1 0 | ||||||
| 1 1 |
Так как столбцы, соответствующие первой и второй формулам, не совпадают, то формулы не являются равносильными. Что касается первой формулы, то она на всех наборах значений переменных принимает значение 1. Такие формулы называются тождественно истинными. Формулы, принимающие значение 0 на всех наборах значений переменных, называются тождественно ложными. Остальные формулы называются выполнимыми.
Аналогично рассмотренному примеру доказывается равносильность следующих формул:
(идемпотентность);
(коммутативность);
(ассоциативность);
(дистрибутивность);
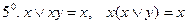(поглощение);
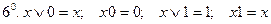
(действия с константами);
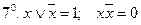(действия с дополнением);
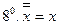(инволютивность);
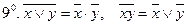(законы де Моргана),
которые остаются верными при подстановке в них вместо независимых переменных любых логических функций. Следовательно, множество булевых функций с операциями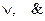 
и отрицания образует булеву алгебру.
Для упрощения формул кроме равносильностей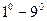 
можно использовать следующие:
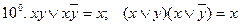(склеивание)
или
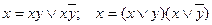(расщепление);
(обобщенное склеивание);
.
Любую булеву функцию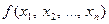 
можно задать с помощью формулы. Если 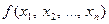не является тождественным нулем, то для нее существует единственная формула специального вида, называемая совершенной дизъюнктивной нормальной формой (СДНФ), которая строится следующим образом.
1. Выбираются наборы значений переменных, на которых функция 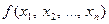равна 1.
2. Каждому такому набору 
сопоставляется так называемая элементарная конъюнкция всех переменных 
, где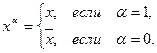 
3. Берутся дизъюнкции всех построенных элементарных конъюнкций.
С помощью равносильных преобразований 
СДНФ можно привести к дизъюнкции элементарных конъюнкций, не обязательно содержащих все переменные. Получим дизъюнктивную нормальную форму (ДНФ). Можно построить разные ДНФ для одной и той же функции.
Пример. Для функции 
построить СДНФ и ДНФ.
Решение. Задание функции трёх переменных в виде последовательности из восьми нулей и единиц означает, что наборы значений переменных берутся в определённом порядке, а именно
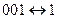
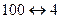
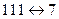
в двоичной записи.
Для построения СДНФ выбираем те наборы значений переменных 
, на которых функция принимает значение 1. Таких наборов пять. Каждому из них соответствует конъюнкция, содержащая каждую переменную или её отрицание. Набору (0,0,0) соответствует 
; отрицания ставятся над теми переменными, которые в данном наборе равны 0;
(0,1,1) ®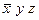 
;
(1,0,0) ® 
;
(1,0,1) ®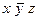 
;
(1,1,0) ® 
.
Поэтому 
.
Упростим эту формулу.
Если вторую элементарную конъюнкцию по идемпотентности повторить несколько раз, а затем применить склеивание, то получим другую ДНФ:
Аналогично, если 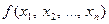не является тождественной единицей, то для нее существует единственная формула специального вида, называемая совершенной конъюнктивной нормальной формой (СКНФ), которая строится следующим образом.
1. Выбираются наборы значений переменных, на которых функция 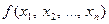равна 0.
2. Каждому такому набору сопоставляется так называемая элементарная дизъюнкция всех переменных 
, где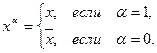
3. Берутся конъюнкции всех построенных элементарных дизъюнкций.
С помощью равносильных преобразований СКНФ можно привести к конъюнкции элементарных дизъюнкций, не обязательно содержащих все переменные. Получим конъюнктивную нормальную форму (КНФ). Можно построить разные КНФ для одной и той же функции.
Пример. Для функции построить СКНФ.
Решение. Для построения СКНФ выбираем те наборы значений переменных , на которых функция принимает значение 0. Таких наборов три. Каждому из них соответствует дизъюнкция, содержащая каждую переменную или её отрицание. Набору (0,0,1) ® 
; отрицание ставится над теми переменными, которые в данном наборе равны 1;
(0,1,0) ® 
; (1,1,1) ®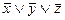 
.
Поэтому 
.
|
Контакты, обозначенные одинаковыми буквами, замыкаются и размыкаются одновременно; при этом, если контакт замыкается, то контакт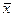 
размыкается и наоборот.
Конъюнкция двух переменных x и y реализуется с помощью схемы
(последовательное соединение контактов),
а дизъюнкция
(параллельное соединение контактов).
Обратно, по схеме можно построить реализуемую ей булеву функцию. Упрощая булеву функцию с помощью эквивалентных преобразований, можно получить более простую контактную схему. Здесь мы имеем простейший пример технической реализации булевых функций. Разным булевым формулам будут соответствовать разные схемы. Чем меньше вхождений букв в булеву формулу, тем проще схема. Поэтому можно вести речь о минимизации булевых формул.
Пример. Упростить контактную схему, используя равносильные преобразования.
Решение. Заданная контактная схема реализует булеву функцию
Следовательно, упрощённая схема имеет вид:
Это достаточно простой пример. Для более сложных случаев применяют специальные методы, в частности, карты Карно.
Картой Карно для логической функции n-переменных называется таблица, состоящая из правильно расположенных квадратов, каждый из которых соответствует одному набору значений независимых переменных, причем соседним квадратам соответствуют наборы, отличающиеся значениями только одной переменной. Квадраты, расположенные в одном ряду по краям таблицы, также считаются соседними. Строки и столбцы, соответствующие значению 1 для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.
По карте Карно как по таблице истинности можно получить СДНФ и СКНФ. Каждый квадрат с единицей определяет элементарную конъюнкцию, содержащую каждую переменную или её отрицание. Если единицы стоят в соседних квадратах, то конъюнкции отличаются одной переменной, которую можно убрать за счёт склеивания.
Чтобы получить дизъюнктивную нормальную форму (ДНФ) по карте Карно заполненные клетки собирают в прямоугольники, состоящие из квадратов. Каждому такому прямоугольнику соответствует один член дизъюнктивной формы, содержащей только те переменные, которые на этом прямоугольнике не меняются, причем если какая-то переменная равна 0, то она входит в конъюнкцию с отрицанием. Минимальной форме соответствует минимальное число максимально возможных прямоугольников.
Аналогично, объединяя пустые квадраты в прямоугольники, получим члены КНФ, содержащие только те переменные, которые на этом прямоугольнике не меняются, причём если какая-то переменная равна 1, то она входит в дизъюнкцию с отрицанием.
Пример. Минимизировать с помощью карты Карно ДНФ и КНФ для функции 
.
Решение. Заполним карту Карно для заданной функции 
, записав 1 в квадратах, соответствующих тем наборам переменных, на которых 
равна 1.
Для данной функции самые большие прямоугольники состоят из 4= 
квадратов (из 6 уже нельзя). Эти прямоугольники выделим с учётом соседства края таблицы. Таких прямоугольников три. То, что они пересекаются, роли не играет. И есть один прямоугольник, состоящий из двух квадратов, который нельзя увеличить. Поэтому минимальная дизъюнктивная форма для функции имеет вид:
Для получения КНФ объединяем пустые квадраты в прямоугольники. Для данной функции пустые прямоугольники состоят, максимум, из двух квадратов, они обведены и не пересекаются.
Минимальная КНФ имеет вид:
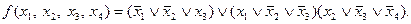
Из рассмотренных примеров видно, что любую булеву функцию можно записать с помощью операций: ‘или’, ‘и’, ‘отрицание’. Но можно использовать и другие логические функции. Наш отечественный математик И.И. Жегалкин предложил использовать для записи произвольных булевых функций константу 1, конъюнкцию и сложение по модулю 2
— 
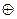, определяемое таблицей истинности:
| x | y | |
Алгебра, построенная на основе этих операций, называется алгеброй Жегалкина и обладает следующими свойствами:
1. 
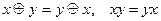коммутативность;
2. 
ассоциативность;
3. 
дистрибутивность умножения относительно сложения;
4. 
свойства констант;
5. 
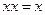закон идемпотентности для умножения;
6. 
закон приведения подобных членов при сложении.
Операции отрицания и дизъюнкции в алгебре Жегалкина записываются формулами:
(1)
, т.е.
(2).
Если в формуле алгебры Жегалкина раскрыть все скобки и произвести упрощения по свойствам 1 — 6, то получится формула, имеющая вид суммы конъюнкций. Такая формула называется полиномом Жегалкина.
Теорема. Для каждой логической функции существует полином Жегалкина, и притом единственный.
Особо важную роль играют функции, полиномы Жегалкина которых имеют вид: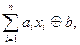 
где 
– константы 0 или 1. Такие функции называются линейными. Все функции от одной переменной – линейные. Среди функций от двух переменных линейных только две: 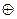— сложение по модулю 2, и ~ (
) — эквиваленция.
Чтобы построить полином Жегалкина для произвольной булевой функции достаточно записать ее ДНФ или КНФ и воспользоваться формулами (1) и (2). Но иногда это проще сделать с помощью метода неопределенных коэффициентов.
Пример: Построить полином Жегалкина для функции .
Решение: Полином Жегалкина для функции трех переменных имеет вид:
.
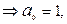
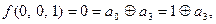
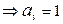
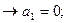
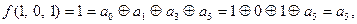
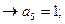
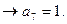
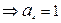
Итак, 
Из рассмотренного выше следует, что все булевы функции можно получить, используя лишь некоторые из них, например, конъюнкцию, дизъюнкцию и отрицание или даже только конъюнкцию и отрицание (дизъюнкцию и отрицание), а можно константу 1, конъюнкцию и сложение по модулю 2, а можно все функции записать с помощью одной операции | (штрих Шеффера) или (стрелка Пирса).
Возможность представления любых булевых функций с помощью ограниченного их числа имеет важное практическое значение при их аппаратной реализации.
Определение. Множество булевых функций 
называют функционально полной системой, если любая логическая функция может быть представлена в виде суперпозиции функций из (формулой над ).
Важную роль в решение задачи о полноте системы имеют замкнутые классы функций, то есть множества функций, суперпозиции которых не выводят за пределы данных множеств. Например, конъюнкция конъюнкций снова конъюнкция, линейная функция от линейных функций снова линейная функция. Особую роль играют замкнутые классы 
:
— множество линейных функций,
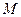— множество монотонных функций,
— множество самодвойственных функций,
— множество функций, сохраняющих 0, т.е. таких, что 
,
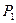— множество функций, сохраняющих 1, т.е. таких, что 
.
Понятие монотонной булевой функции несколько отличается от одноименного понятия в анализе. На множестве двоичных векторов или наборов значений 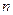переменных 
, 
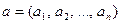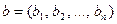вводится отношение частичного порядка: 
, если существует 
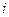такое, что 
, а для остальных индексов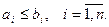 
Определение. Функция 
называется монотонной, если для любых двоичных 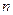-мерных векторов 
и 
из того, что , следует, что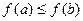 
.
Если для некоторой функции 
, а 
, для какого-нибудь , то эта функция уже не монотонна. По таблице булевых функций двух переменных видно, что монотонны 0, 1, Ú, Ù, , , в то время как 
, , 
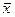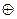, , |, не являются монотонными.
Для проверки монотонности можно пользоваться следующим критерием:
Теорема. Булева функция, отличная от 0 и 1, монотонна тогда и только тогда, когда существует представляющая ее булева функция без отрицаний (т.е. функция выражается через конъюнкцию и дизъюнкцию своих переменных).
Если получить такую формулу не удается, то, возможно, что функция не монотонна, т.е. найдутся такие наборы и , что , а 
. Эти наборы следует явно указать.
Пример. Функция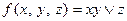 
монотонна по критерию, а про функцию 
сразу ничего сказать нельзя, так как наличие в формуле отрицания еще не означает, что нет другой булевой формулы без отрицания. Однако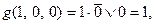 
, а 
, следовательно, функция не монотонна.
Определение. Функция называется самодвойственной, если 
для всех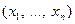 
.
Из определения следует, что функция не является самодвойственной, если найдется такой набор 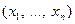, что 
. При векторном задании функции самодвойственность или несамодвойственность очевидны: функция самодвойственна, если вектор антисимметричен относительно своей середины 
, и несамодвойственна в противном случае.
Пример.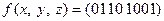 
самодвойственна, а 
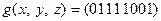несамодвойственна, так как 
Американским математиком Э. Постом (1897-1954) доказана следующая
Теорема. Для полноты системы функций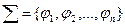 
необходимо и достаточно, чтобы для каждого из классов в 
нашлась функция 
, не принадлежащая этому классу.
Пример. Проверить. является ли функционально полной система 
.
Решение. Составим таблицу, в которой будем отмечать “непринадлежность” функции классам, указанным в теореме Поста.
|
|
|
|
|
| 
|
|
| - | - | - | - | + |
| + | + | - | + | - |
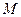
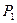
1. Функция 
.
Найдем для нее полином Жегалкина. Это можно сделать методом неопределенных коэффициентов, а можно непосредственно переписывая отрицание и дизъюнкцию через операции алгебры Жегалкина:
Функция 
не является линейной (есть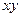 
).
, а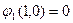 
— это противоречит определению монотонности, следовательно, не является монотонной.
, т.е. 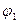не сохраняет 0.
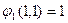, т.е. 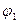сохраняет 1.
, т.е.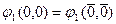 
, значит, 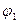не является самодвойственной.
2. Функция 
.
линейная (нет конъюнкции).
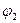монотонна, т.к. для всех 
.
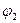, сохраняет 0.
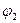, несохраняет 1.
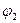, не является самодвойственной.
По таблице видим, что для каждого из классов нашлась функция, ему не принадлежащая, значит å – функционально полная система.
Если из системы убрать , то останется 0, который один не дает функционально полной системы (он принадлежит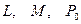 
); если же убрать 0, то останется , которая сохраняет 1. Поэтому система å образует базис.
Замечание:
1. Ранее отмечалось, что из функций двух переменных только Å и линейные, поэтому нелинейность можно было определить сразу.
2. После того, как таблица заполнена для первой функции, для второй достаточно было проверить лишь принадлежность или непринадлежность ее классу .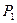
Рассмотренные вопросы можно изучить по указанной литературе, точнее: [3, гл. 1, § 1.1—1.6, гл. 5, §5.1—5.5], [4, гл. 3, § 1—12], [6, гл. 3, § 3.1—3.3], [7, разд. 2, гл. 4, § 4,3—4.5], [8, гл. 1, § 1.1—1.2], [9, гл. 3], [11, гл. 6, § 6.1—6.9], [12, ч. 1, гл. 1].