Лекция 1.
Геометрические векторы.
Вопрос № 1. Координаты на прямой, числовая ось.
Рассмотрим произвольную прямую. На этой прямой можно указать два взаимно противоположных направления. Выберем одно из них. На рисунке будем обозначать это направление стрелкой.

Пусть, кроме этого, выбрана масштабная единица для измерения длин отрезков.
Определение. Прямая линия, с выбранным на ней направлением и единицей масштаба, называется координатной осью.
Рассмотрим на оси две произвольные точки  и
и  .
.
Определение. Отрезоксграничными точками  и
и  называется направленным, если указано, какая из точек
называется направленным, если указано, какая из точек  и
и  считается началом, а какая – концом отрезка.
считается началом, а какая – концом отрезка.
Длина направленного отрезка  обозначается так
обозначается так 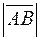 .
.
Определение. Величиной 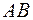 направленного отрезка
направленного отрезка  называется число, равное
называется число, равное 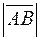 , если направление отрезка и оси совпадают, и равное
, если направление отрезка и оси совпадают, и равное 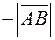 , если эти направления противоположны.
, если эти направления противоположны.
Если точки  и
и  совпадают, то величину направленного отрезка
совпадают, то величину направленного отрезка  считаем равной нулю.
считаем равной нулю.
Утверждение. Для любых трех точек  и
и  на оси справедливо основное тождество
на оси справедливо основное тождество 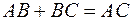 .
.
Определение. Числовой осью называется прямая линия, на которой зафиксирована точка 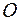 , называемая началом координат, выбраны положительное направление и единица длины.
, называемая началом координат, выбраны положительное направление и единица длины.
Каждому действительному числу однозначно соответствует точка на оси координат.
Пусть точка 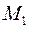 имеет координату
имеет координату 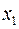 , а точка
, а точка  - координату
- координату  . Величина
. Величина  направленного отрезка
направленного отрезка  равна
равна 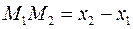 .
.
Вопрос № 2. Прямоугольная система координат.
Определение. Две взаимно перпендикулярные оси  и
и 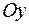 , имеющие общее начало
, имеющие общее начало 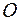 и одинаковую масштабную единицу, образуют прямоугольную систему координат на плоскости.
и одинаковую масштабную единицу, образуют прямоугольную систему координат на плоскости.

Ось  называется осью абсцисс, ось
называется осью абсцисс, ось 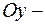 осью ординат, а обе оси вместе – осями координат.
осью ординат, а обе оси вместе – осями координат.
Прямоугольными координатами  и
и 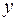 точки
точки  называются величины направленных отрезков
называются величины направленных отрезков 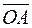 и
и  :
: 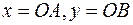 .
.
Координаты  и
и 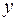 точки
точки  называются ее абсциссой и ординатой.
называются ее абсциссой и ординатой.
Оси координат разбивают плоскость на части, их называют четвертями и номеруют римскими цифрами I, II, III, IV.
Определение. Прямоугольная система координат  в пространстве определяется заданием масштабной единицы измерения длин и трехпересекающихсяв одной точке
в пространстве определяется заданием масштабной единицы измерения длин и трехпересекающихсяв одной точке 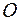 взаимно перпендикулярных осей.
взаимно перпендикулярных осей.
Координаты  и
и  точки
точки  называются ее абсциссой, ординатой и аппликатой.
называются ее абсциссой, ординатой и аппликатой.
Вопрос № 3. Геометрические векторы.
Определение. Направленный отрезок называется геометрическим вектором.
Обозначение. Вектор обозначается символом  (или
(или  ), причем первая буква означает начало вектора, а вторая – его конец.
), причем первая буква означает начало вектора, а вторая – его конец.
Определение. Вектор  называется противоположным вектором к вектору
называется противоположным вектором к вектору  .
.
Определение. Длинойвектора  называется длина направленного отрезка
называется длина направленного отрезка  и обозначается
и обозначается  .
.
Определение. Вектор,у которого начало и конец совпадают, называется нулевым вектором.
Обозначение. Нулевой вектор:  или
или  .
.
Нулевой вектор имеет произвольное направление, его длина равна нулю.
Определение. Векторы 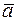 и
и  называются равными (
называются равными (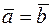 ) если они коллинеарны, одинаково направлены и их длины раны.
) если они коллинеарны, одинаково направлены и их длины раны.
Совокупность всех равных векторов называют свободным вектором.
Пусть заданы ось 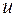 и некоторый вектор
и некоторый вектор  . Через точки
. Через точки  и
и  проведем плоскости, перпендикулярные оси
проведем плоскости, перпендикулярные оси 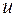 . Обозначим через
. Обозначим через 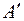 и
и 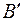 точки пересечения этих плоскостей с осью
точки пересечения этих плоскостей с осью 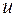 .
.

Определение. Проекцией вектора  на ось
на ось 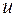 называется величина
называется величина  направленного отрезка
направленного отрезка  на оси
на оси 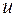 .
.
Обозначение. Проекция вектора  на ось
на ось 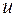 :
:  .
.
Утверждение 1.  , где
, где 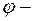 угол между вектором
угол между вектором  и осью
и осью 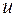 .
.

Утверждение 2. Равные векторы имеют равные проекции на одну и ту же ось.
Пусть в пространстве заданы прямоугольная система координат  и произвольный вектор
и произвольный вектор  . Пусть также
. Пусть также 
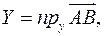
 .
.
Утверждение 3. 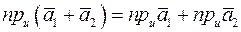 .
.
Утверждение 4.  .
.
Определение. Проекции  вектора
вектора  на оси координат называют его координатами.
на оси координат называют его координатами.
Обозначение.  .
.
Утверждение 5. Для любых двух точек 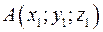 и
и 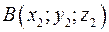 координаты вектора
координаты вектора  определяются соотношениями:
определяются соотношениями: 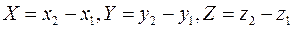 .
.
Утверждение 6. Есливектор  выходит из начала координат, то координаты вектора
выходит из начала координат, то координаты вектора  равны координатам его конца:
равны координатам его конца:  , здесь
, здесь  и
и  .
.
Пусть задан произвольный вектор 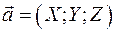 , выходящий из начала координат и не лежащий ни в одной координатной плоскости. Проведем через точку
, выходящий из начала координат и не лежащий ни в одной координатной плоскости. Проведем через точку  плоскости, перпендикулярные осям. Вместе с координатными плоскостями они образуют прямоугольный параллелепипед, диагональю которого служит отрезок
плоскости, перпендикулярные осям. Вместе с координатными плоскостями они образуют прямоугольный параллелепипед, диагональю которого служит отрезок 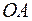 .
.

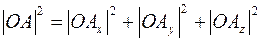
Следовательно

Обозначим через  углы между вектором
углы между вектором 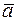 и осями координат. Тогда из «Утверждения 1» следует
и осями координат. Тогда из «Утверждения 1» следует
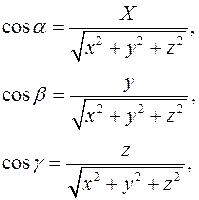
Определение. 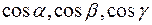 называются направляющими косинусами вектора
называются направляющими косинусами вектора 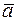 .
.
Утверждение 4. 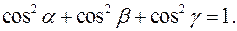
Вопрос № 4. Линейные операции над геометрическими векторами.
Пусть даны два вектора 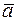 и
и  .
.
Определение. Суммой  называется вектор, который идет из начала вектора
называется вектор, который идет из начала вектора 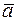 в конец вектора
в конец вектора  при условии, что вектор
при условии, что вектор  приложен к концу вектора
приложен к концу вектора 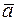 .
.

Утверждение 1.
Если  и
и  , то
, то  .
.
Пусть даны вектор 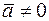 и число
и число 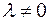 .
.
Определение. Произведением  называется вектор, который коллинеарен вектору
называется вектор, который коллинеарен вектору 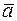 , имеет длину, равную
, имеет длину, равную  , и направление такое же, как вектор
, и направление такое же, как вектор 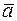 , если
, если 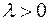 , и противоположное, если
, и противоположное, если 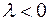 .
.

Утверждение 2. Если векторы 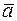 и
и  коллинеарны и
коллинеарны и 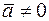 , то существует единственное число
, то существует единственное число  такое, что
такое, что 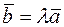 .
.
Основные свойства линейных операций.
1. 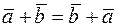 (переместительное свойство сложения)
(переместительное свойство сложения)
2.  (сочетательное свойство сложения)
(сочетательное свойство сложения)
3.  (сочетательное свойство умножения)
(сочетательное свойство умножения)
4.  (распределительное свойство относительно суммы чисел)
(распределительное свойство относительно суммы чисел)
5.  (распределительное свойство относительно суммы векторов)
(распределительное свойство относительно суммы векторов)
Эти свойства дают возможность производить над векторами обычные алгебраические действия.
Определение. Векторы 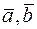 и
и  называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Вопрос № 5. Базисы и координаты.
Определение. На плоскости два любых не коллинеарных вектора  и
и  называются базисом.
называются базисом.
Утверждение 1. Любой вектор  на плоскости может быть представлен как линейная комбинация векторов базиса
на плоскости может быть представлен как линейная комбинация векторов базиса 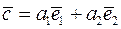 .
.
Пусть векторы  единичные векторы осей координат на плоскости. Это означает, что
единичные векторы осей координат на плоскости. Это означает, что
 ,
,
и каждый из них одинаково направлен с ответствующей осью координат.
Утверждение 2. Совокупность векторов 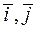 является единичным ортогональным базисом на плоскости.
является единичным ортогональным базисом на плоскости.
Пусть векторы  единичные векторы осей координат. Это означает, что
единичные векторы осей координат. Это означает, что
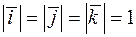 ,
,
и каждый из них одинаково направлен с ответствующей осью координат.
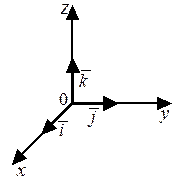
Определение. Тройка векторов  называется базисом.
называется базисом.
Утверждение 3. Любой вектор 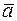 может быть единственным образом разложен по базису
может быть единственным образом разложен по базису  , то есть, представлен в виде
, то есть, представлен в виде
 ,
,
где  некоторые числа (координаты вектора).
некоторые числа (координаты вектора).
Рассмотрим вектор 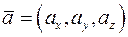 , для которогочисла
, для которогочисла 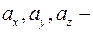 координаты этого вектора в базисе
координаты этого вектора в базисе  .
.
Утверждение 4. Если начало вектора 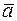 совпадает с началом координат, то координаты его конца равны координатам вектора
совпадает с началом координат, то координаты его конца равны координатам вектора 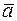 .
.
Утверждение 5. Координаты вектора в данном базисе равны разностям одноименных координат его конца и начала в системе координат, определенной данным базисом.
Утверждение 6. Если вектор 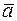 задан своими координатами
задан своими координатами  , то противоположный ему вектор имеет координаты
, то противоположный ему вектор имеет координаты 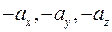 , то есть
, то есть  .
.
Таким образом вектором в  можно называть любую упорядоченную тройку чисел
можно называть любую упорядоченную тройку чисел  .
.
Лекция 2.
Умножения геометрических векторов.
Определение. Скалярным произведением двух ненулевых векторов 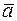 и
и  называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними.
называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними.
Если хотя бы один из векторов равен нулю, то угол не определен и скалярное произведение равно нулю.
Обозначение. Скалярное произведение векторов 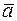 и
и 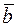 обозначают
обозначают  ,
,
 ,
,
где  угол между векторами
угол между векторами 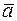 и
и 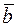 .
.