Лекция 6.
Определители.
Определение. Определителем квадратной матрицы
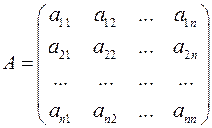
называется число, которое может быть вычислено по элементам матрицы по формуле:
 ,
,
где 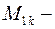 минор матрицы, определитель полученной из исходной вычеркиванием первой строки и
минор матрицы, определитель полученной из исходной вычеркиванием первой строки и  столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Предыдущая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:

Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:

 , i = 1,2,…,n.
, i = 1,2,…,n.
Очевидно, что различные матрицы могут иметь одинаковые определители.
Определитель единичной матрицы равен 1.
Для указанной матрицы  число
число 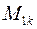 называется дополнительным минором элемента матрицы
называется дополнительным минором элемента матрицы  . Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
Определение. Дополнительный минор произвольного элемента квадратной матрицы 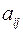 равен определителю матрицы, полученной из исходной вычеркиванием
равен определителю матрицы, полученной из исходной вычеркиванием  ой строки и
ой строки и  го столбца.
го столбца.
Свойство 1. Важным свойством определителей является следующее соотношение:
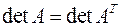 .
.
Свойство 2. 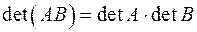 .
.
Свойство 3. Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.
Свойство 4. При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.
Определение: Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.
Свойство 6. Если в матрице  строки или столбцы линейно зависимы, то ее определитель равен нулю.
строки или столбцы линейно зависимы, то ее определитель равен нулю.
Свойство 7. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)
Свойство 8. Определитель матрицы не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.
Свойство 9. Если для элементов какой- либо строки или столбца матрицы верно соотношение:  ,
,  ,
,  , то верно:
, то верно:

Пример. Вычислить определитель матрицы  .
.

= -5 + 18 + 6 = 19.
Пример. Даны матрицы  , В =
, В = 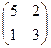 . Найти
. Найти  .
.
1)  ;
;  ;
;  .
.
1) 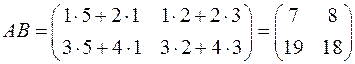 ;
; 
Элементарные преобразования матрицы.
Элементарными преобразованиями матрицы назовем следующие преобразования:
1) умножение строки на число, отличное от нуля;
2) прибавление к элементам одной строки элементов другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
5) транспонирование;
Те же операции, применяемые для столбцов, также называются элементарными преобразованиями.
С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк (столбцов).
Миноры.
Выше было использовано понятие дополнительного минора матрицы. Дадим определение минора матрицы.
Определение. Если в матрице  выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.
выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.
Заметим, что вышесказанное применимо не только к квадратным матрицам, но и к прямоугольным.
Если вычеркнуть из исходной квадратной матрицы  выделенные строки и столбцы, то определитель полученной матрицы будет являться дополнительным минором.
выделенные строки и столбцы, то определитель полученной матрицы будет являться дополнительным минором.
Алгебраические дополнения.
Алгебраическим дополнением минора матрицы называется его дополнительный минор, умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов минора матрицы.
В частном случае, алгебраическим дополнением элемента матрицы называется его дополнительный минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.
Теорема Лапласа.
Если выбрано  строк матрицы с номерами
строк матрицы с номерами  , то определитель этой матрицы равен сумме произведений всех миноров, расположенных в выбранных строках на их алгебраические дополнения.
, то определитель этой матрицы равен сумме произведений всех миноров, расположенных в выбранных строках на их алгебраические дополнения.
Обратная матрица.
Определим некоторую операцию над матрицами как операцию, обратную к умножению матриц.
Определение. Если существуют квадратные матрицы  и
и  одного порядка, удовлетворяющие условию:
одного порядка, удовлетворяющие условию:
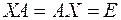 ,
,
где  единичная матрица того же самого порядка, что и матрица
единичная матрица того же самого порядка, что и матрица  , то матрица
, то матрица  называется обратной матрицей к матрице
называется обратной матрицей к матрице  и обозначается
и обозначается  .
.
Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.
Рассмотрим общий подход к нахождению обратной матрицы.
Исходя из определения произведения матриц, можно записать:
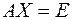 Þ
Þ 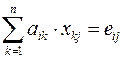 ,
,  ,
,
причем

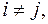 и
и 
 .
.
Таким образом, получаем систему уравнений:
 ,
,
Решив эту систему, находим элементы матрицы  .
.
Пример 1. Дана матрица  , найти
, найти  .
.
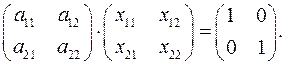

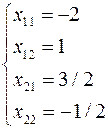
Таким образом,  .
.
Однако, такой способ не совсем удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:
 ,
,
где 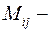 дополнительный минор элемента
дополнительный минор элемента 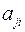 матрицы
матрицы  .
.
Другими словами
 ,
,
где 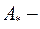 союзная матрица, матрица, составленная из алгебраических дополнений
союзная матрица, матрица, составленная из алгебраических дополнений  - дополнительных миноров элемента
- дополнительных миноров элемента 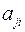 матрицы
матрицы  снабженных знаком
снабженных знаком 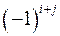
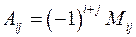
Пример 2. Дана матрица  , найти
, найти  .
.
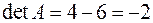 .
.

 ,
, 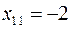 ;
;

 ,
,  ;
;

 ,
,  ;
;

 ,
, 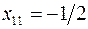 ;
;
Таким образом,  .
.