Всякий многочлен f(x) степени n имеет 
корней и может быть записан в виде
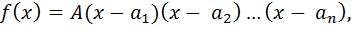(1)
где А – коэффициент при 
– корни многочлена. Если многочлен с действительными коэффициентами имеет корень а = 
, то он имеет и корень 
. Но (x – a)(x -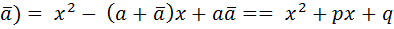 
, где p, q – действительные числа. Объединим в (1) одинаковые множители. Получим
f(x) = A 
(2)
Здесь 
- действительные корни, каждый трехчлен имеет только комплексные корни.
Пусть P(x) и Q(x) – многочлены с действительными коэффициентами. Рациональная дробь 
называется правильной, если степень числителя меньше степени знаменателя. Если не является правильной, то, разделив P(x) на Q(х), получим 
, где R(x) – многочлен, 
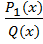– правильная дробь.
Определение 1. Дроби вида 
где A,M,N – постоянные числа, k, 
– натуральные числа, 
не имеет действительных корней, называются простейшими или элементарными.
Теорема 1. Правильная дробь может быть представлена в виде суммы элементарных дробей. При этом если в разложении Q(x) входит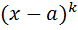 
, то такому множителю соответствует сумма элементарных дробей вида
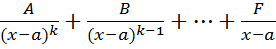; каждому множителю вида 
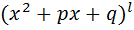соответствует сумма элементарных дробей вида
, где 
– постоянные числа. (Л.Д. Кудрявцев. Математический анализ, т.1.).
Пусть нужно вычислить 
, где P(x) и Q(x) многочлены с действительными коэффициентами. Если – неправильная дробь, то сначала выделим целую часть, т.е. 
= 
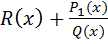, где 
– правильная дробь. Разложим ее на элементарные дроби. Задача интегрирования рациональных функции свелась к интегрированию элементарных дробей вида
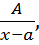
1) 
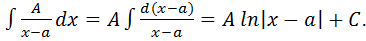
2) 
3) 
t = x 
dt = dx
q - 
= 
= 
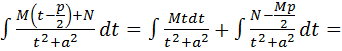
Здесь 
4) 
= 
Вычислим 
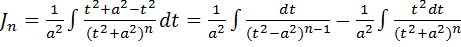
Второй интеграл берется по частям: u=t;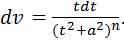 
. Так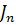 
сводим к 
, затем 
сводим так же к 
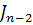и так далее, пока не получим 
Пример. 
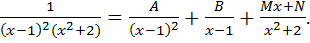
1 = 
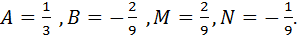
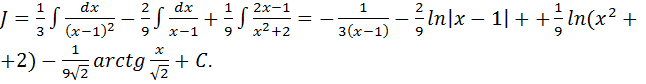
Существует метод Остроградского, который позволяет избежать интегрирования дробей вида 4) (Кудрявцев Л.Д, т.1, параграф 24).
Интегрирование простейших
Иррациональных функций.
I. 
R(x,y) – рациональная функция.
Получаем интеграл от рациональной функции.
Пример 1. 
= 
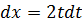
II. 
Подстановки Эйлера.
1) 
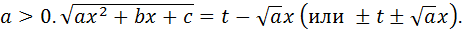
Получаем интеграл от рациональной функции.
2) 
(или 
Снова интеграл от рациональной функции.
3)Корни трехчлена действительны. 
- любой из корней.
Пример 2. 
.
III. Подстановки Эйлера позволяют вычислить любой интеграл вида II. Однако при их использовании приходится прибегать к громоздким вычислениям. Поэтому подстановки Эйлера нужно применять лишь тогда, когда интеграл не берется более коротким путем.
В некоторых случаях можно обойтись без подстановок Эйлера.
. Положим 
. Тогда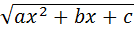 
в зависимости от знаков 
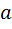и 
сведется к одному из видов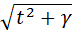 
или 
. Таким образом, можно ограничиться рассмотрением 
и 
.
1) 
2) 
3) 
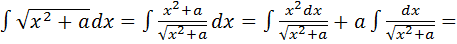
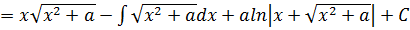
4) 
берется как 3)
5) 
Полагаем 
IV. Интегралы от дифференциального бинома.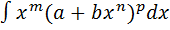 
(
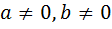, m, n, p – рациональные числа)
Если одно из чисел 
– целое, то интеграл сводится к интегралу от рациональной функции. В остальных случаях этот интеграл в элементарных функциях не выражается(П.Л.Чебышев).
1) p – целое. Если 
2) 
.
3) 
.
Пример 3. 
= 
+ 
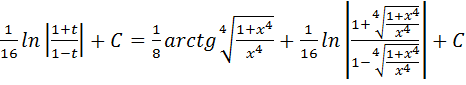
84. Интегрирование простейших
трансцендентных функций
I.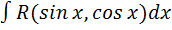 
Подстановка 
сводит его к интегралу от рациональной функции. Действительно 
Пример 1.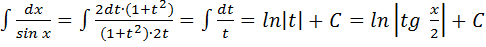 
Подстановка 
является универсальной, но связана с громоздкими вычислениями.
II. 
1) p,q – рациональные числа. Интеграл сводится к интегралу от дифференциального бинома, например подстановкой 
или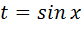 
.
2) 
– нечетное натуральное число. 
3) 
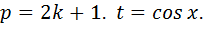
4) p= 
a) 
б) 
5) 
– четное отрицательное число.
6) p и q – четные натуральные числа.
Переходим к двойному углу: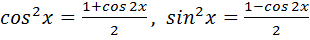 
Пример 2.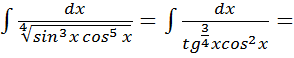 
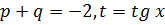
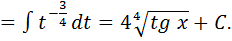
III. 
IV. 
где 
– многочлен,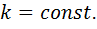 
По частям, 
V.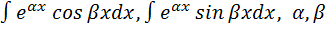 
– действительные числа. По частям.
VI.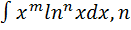 
– натуральное число. 
Приходим к IV.
VII.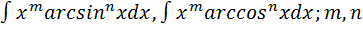 
– натуральные числа.
В первом интеграле 
. Далее по частям: 
.