Геометрическая интерпретация комплексного числа
Комплексное число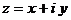 
изображается точкой с координатами (х; y) в декартовой системе координат XOY, при этом каждому комплексному числу соответствует некоторая точка координатной плоскости и каждой точке координатной плоскости соответствует некоторое комплексное число.
Определение 5. Плоскость, точки которой отождествлены с комплексными числами, называется комплексной плоскостью. В этом случае ось абсцисс называется действительной осью, так как служит для изображения действительных чисел. Ось ординат называется мнимой осью, так как ее точки изображают чисто мнимые комплексные числа yi. Начало координат, точка 0 служит изображением нуля.
Модуль и аргумент комплексного числа.
Тригонометрическая форма комплексного числа
Определение 6. Модулем комплексного числа 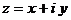(обозначение: 
или r) называется длина радиуса – вектора 
.
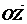Свойства модуля комплексного числа:
1. 
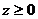
2. 
.
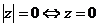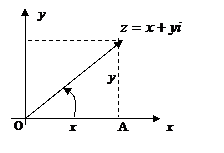
Из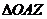 
:
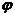
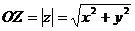. (1)
Рис. 3.
Определение 7. Аргументом комплексного числа z (z¹ 0) называется угол образованный положительным направлением оси OX и лучом OZ отсчитываемый против часовой стрелки. Обозначение: Arg z.
Заметим, что аргумент комплексного числа z определен не однозначно, так как угол между двумя направлениями может отсчитываться многими способами. Все значения аргумента задаются формулой:
  ,
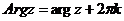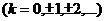| (2) |
|
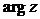- главное значение аргумента, задаваемое следующими условиями
|
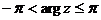(или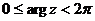 
|
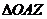(рис. 3).
I способ: Пусть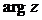 
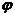= , тогда 
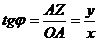откуда
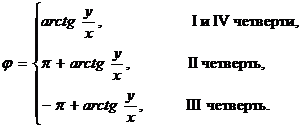
| (3) |
II способ: Пусть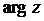 
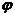= , тогда
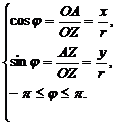
| (4) |
Тригонометрическая форма комплексного числа
Пусть дано комплексное число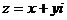 
, 
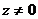. Из 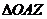(рис. 3) имеем: 
, 
, 
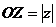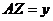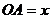и
 , 
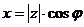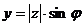
| (5) |
Подставив в комплексное число 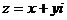соотношения (5) получим новую запись комплексного числа
  +   .
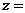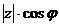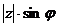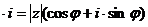| (6) |
Определение 8. Запись комплексного числа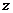 
в ви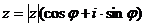де 
, где - модуль комплексного числа 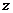, 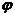- одно из значений аргумента, называется тригонометрической формой комплексного числа .
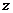Любое комплексное число 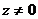можно записать в тригонометрической форме и обратно, любое число записанное в тригонометрической форме можно представить в алгебраической форме или в ее какой-нибудь другой форме. При этом любая запись вида 
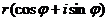, где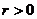 
есть некоторое комплексное число в тригонометрической форме.
Определение 9. Два комплексных числав тригонометрической форме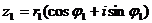 
и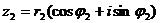 
равны тогда и только тогда, когда равны их модули и аргументы 
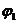и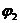 
отличаются на целое, кратное 2π: 
, 
.
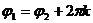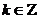Показательная форма комплексного числа
В математике и ее приложениях часто встречается выражение вида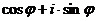 
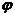( - вещественное число). Для него используют различные сокращенные обозначения. Например, в картографии его обозначают знаком 
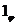, в электротехнике – знаком 
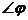, а в работах по математике – через 
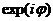или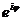 
. Таким образом, по определению
 .
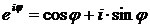| (11) |
Через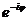 
обозначают число
 .
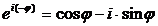| (12) |
Обозначение (11) оправдано сходством свойств выражений вида 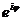со свойствами показательной функции. Например, при любых вещественных 
, 
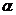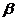и 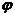справедливы следующие формулы:
,
,
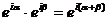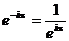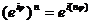(n – любое целое число).
Последняя формула представляет собой формулу Муавра:
.
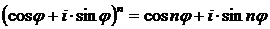Из (11) и (12) легко выводятся формулы:
, 
.
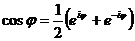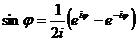Определение 10. Соотношение (11) называется формулой Эйлера и позволяет каждое комплексное число 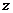записать в виде (показательная форма)
 ,
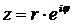| (13) |
где 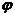- аргумент числ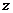а , а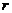 
- его модуль.