Тождества
Пример 1
Найдем значения двух алгебраических выражений х 2 и 5 х – 6 при одном и том же значении переменной, например х = 1. Получаем значения этих выражений: (1)2= = 1 и 5 ∙ 1 – 6 = 5 – 6 = –1. Видно, что соответственные значения выражений не равны. Теперь найдем соответственные значения этих выражений при х = 2. Получаем значения: (2)2 = 4 и 5 ∙ 2 – 6 = 10 – 6 = 4. В этом случае значения выражений равны.
Существуют и такие выражения, соответственные значения которых равны при любых допустимых значениях. Такие выражения называются тождественно равными.
Пример 2
а) В соответствии с переместительным и сочетательным свойствами сложения выражения a + b + c; b + a + c; (a + b) + c; a + (b + c); (a + c) + b и т.д. являются тождественно равными при всех значениях a, b и с.
б) В соответствии с основным свойством дроби выражения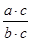 
и 
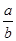являются тождественно равными при всех допустимых значениях переменных a, b и с, т.е. при любых значениях a, b (кроме b = 0) и с (кроме с = 0), или при b ≠ 0 и с ≠ 0.
в) В соответствии с основным свойством дроби выражения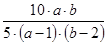 
и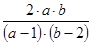 
являются тождественно равными при а ≠ 1 и b ≠ 2.
Равенство, связывающее два тождественно равных выражения, называется тождеством.
Пример 3
Являются тождествами при всех допустимых значениях переменных равенства:
а) a + b + c = a + (b + c);
б)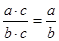 
;
в) = .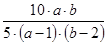
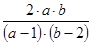Верные числовые равенства также считаются тождествами.
Пример 4
Являются тождествами равенства:
а) (32 – 5): 4 = 2 – 1;
б) (1 + 2 + 3 + 4): 5 = 22 – 2.
Тождественные преобразования выражений
Пример 1
Используя распределительное свойство, при всех значениях переменных найдем значение выражения:
a ∙ (b – c) + b ∙ (c – a) + c ∙ (a – b) = a ∙ b – a ∙ c + b ∙ c – c ∙ a – c ∙ b = (a ∙ b – b ∙ a) + + (– a ∙ c + c ∙ a) + (b ∙ c – c ∙ b) = 0 + 0 + 0 = 0.
При решении задачи выло также использовано переместительное свойство b ∙ a = a ∙ b, c ∙ a = a ∙ c, c ∙ b = b ∙ c – и сочетательное свойство. В результате вычислений и замены выражений тождественно равными было получено, что при всех значениях переменных a, b и с данное громоздкое выражение a ∙ (b – c) + b ∙ ∙ (c – a) + c ∙ (a – b) равно 0.
Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения.
Тождественные преобразования выражений выполняются с применением свойств действий над числами (включая дроби).
2. Правила выполнения тождественных преобразований
Тождественные преобразования выражений используется при решении многих алгебраических задач. С некоторыми тождественными преобразованиями вы уже знакомы: приведение подобных членов, раскрытие скобок, сокращение дробей. Напомним правила выполнения подобных преобразований.
1. При приведении подобных членов надосложить их коэффициенты и результат умножить на общую буквенную часть этих членов.
Пример 2
Используя распределительное свойство, приведем подобные члены в выражении:
7 ∙ а ∙ b – 3 ∙ a ∙ b + 2 ∙ a ∙ b – 5 ∙ a ∙ b = a ∙ b ∙ (7 – 3 + 2 – 5) = a ∙ b ∙ 1 = ab
2. Если перед скобками стоит знак «плюс», то скобки опускаются, сохраняя знак каждого слагаемого, входящего в скобки.
Пример 3
Раскроем скобки, используя сочетательное свойство, в выражении:
5 ∙ а 2 + (7 ∙ b – 2 ∙ c 2) = 5 ∙ а 2 + 7 ∙ b – 2 ∙ c 2.
3. Если перед скобками стоит знак «минус», то скобки опускают, изменяя знак каждого слагаемого, входящего в скобки, на противоположный.
Пример 4
Раскроем скобки, используя приведенное правило, в выражении:
5 ∙ а 2 – (7 ∙ b – 2 ∙ c 2) = 5 ∙ а 2 – 7 ∙ b + 2 ∙ c 2.
При этих преобразованиях были использованы распределительное и сочетательное свойства. Второе слагаемое (7 ∙ b – 2 ∙ c 2) можно записать в виде произведения (–1) ∙ (7 ∙ b – 2 ∙ c 2). Тогда получаем 5 ∙ а 2 – (7 ∙ b – 2 ∙ c 2) = 5 ∙ а 2 + (–1) ∙ ∙ (7 ∙ b – 2 ∙ c 2) = 5 ∙ а 2 – 7 ∙ b + 2 ∙ c 2.
4. При сокращении дроби ее числитель и знаменатель можно разделить на одно и то же выражение, не равное нулю.
Пример 5
Сократим дробь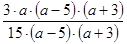 
. Для этого ее числитель и знаменатель разделим на выражение 3 ∙ (а – 5) ∙ (а + 3) (при этом а ≠ 5 и а ≠ –3) и получим 
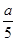. Выражения 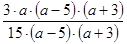и 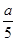тождественно равны при всех допустимых значениях переменных, т.е. а ≠ 5 и а ≠ –3.