Уже простейшие алгебраические операции над действительными числами (извлечение квадратного корня из отрицательного числа, решение квадратного уравнения с отрицательным дискриминантом) выводят за пределы множества действительных чисел. Дальнейшее обобщение понятия числа приводит к комплексным числам. Замечательным свойством множества комплексных чисел является его замкнутость относительно основных математических операций. Иначе говоря, основные математические операции над комплексными числами не выводят из множества комплексных чисел.
Комплексным числом 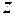 (в алгебраической форме) называется выражение
(в алгебраической форме) называется выражение
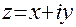
где 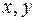 – произвольные действительные числа,
– произвольные действительные числа, 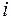 – мнимая единица, определяемая условием
– мнимая единица, определяемая условием 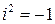 .
.
Число 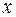 называется действительной частью комплексного числа
называется действительной частью комплексного числа 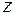 , обозначается
, обозначается 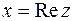 (от латинского «realis »), число
(от латинского «realis »), число 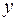 называется мнимой частью комплексного числа
называется мнимой частью комплексного числа 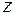 и обозначается
и обозначается 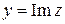 (от латинского «imaginarius »).
(от латинского «imaginarius »).
Два комплексных числа 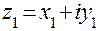 и
и 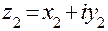 равны тогда и только тогда, когда равны их действительные и мнимые части:
равны тогда и только тогда, когда равны их действительные и мнимые части: 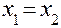 ,
, 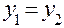 . Два комплексных числа равны либо не равны (понятия «больше» и «меньше» для комплексных чисел не вводятся).
. Два комплексных числа равны либо не равны (понятия «больше» и «меньше» для комплексных чисел не вводятся).
Комплексно-сопряженным к числу 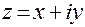 называется число
называется число 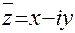 . Очевидно, комплексно–сопряженное число к числу
. Очевидно, комплексно–сопряженное число к числу 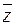 совпадает с числом
совпадает с числом 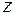 :
: 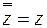 .
.
Арифметические операции. Сложение, вычитание и умножение комплексных чисел производят по обычным правилам алгебры.
Пусть 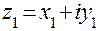 ,
, 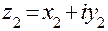 . Тогда
. Тогда
сумма 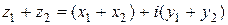 ,
,
разность 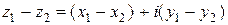 ,
,
произведение 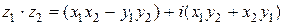 ,
,
частное (при 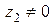 )
)

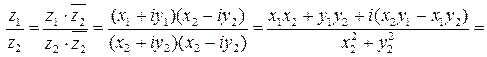
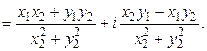

Пример 1. Заданы комплексные числа 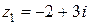 ,
, 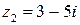 .
.
Найти 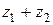 ,
, 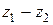 ,
, 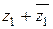 .
.
Решение. 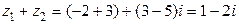 ;
;
 ;
;
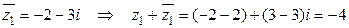 .
.
Пример 2. Найти 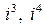 ,
, 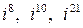 .
.
Решение. 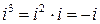 ;
; 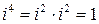 .
.
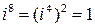 ,
, 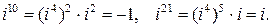
Замечание. Степени числа 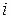 можно представить в виде таблицы
можно представить в виде таблицы
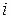
| 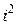
| 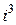
| 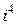
| 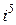
| 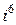
| 
| 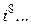
|
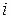
| 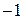
| 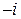
| 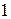
| 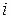
| 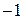
| 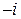
| 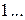
|
Пример 3. Перемножить числа 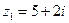 и
и 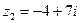 .
.
Решение. 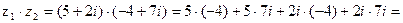
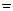
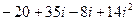
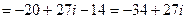
Пример 4. Вычислить а) 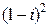 ; б)
; б) 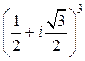 ; в)
; в) 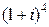 .
.
Решение.
а) Раскроем квадрат разности:
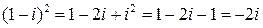 .
.
б) Раскроем куб суммы:
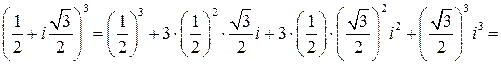
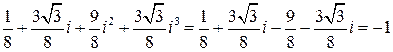 .
.
в) 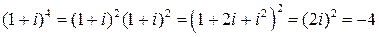 .
.
Пример 5. Найти частное 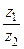 , если
, если 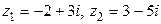 .
.
Решение.
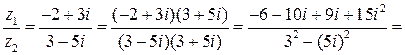
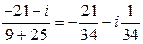 .
.
Пример 6. Вычислить а) 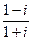 , б)
, б)  .
.
Решение. а) 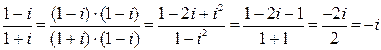 .
.
б) 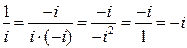 .
.
Запомним: 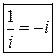
2 Геометрическая интерпретация комплексного ч исла.
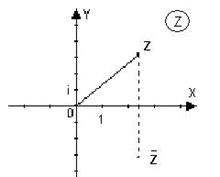
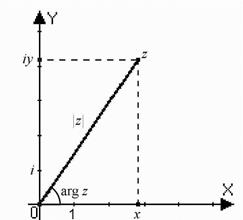
Рассмотрим декартову прямоугольную систему координат. Отложим по оси абсцисс действительную часть 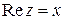 комплексного числа
комплексного числа 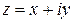 , а по оси ординат – его мнимую часть
, а по оси ординат – его мнимую часть 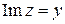 . Получим точку с координатами
. Получим точку с координатами  . При этом каждому комплексному числу
. При этом каждому комплексному числу 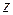 соответствует одна точка плоскости. Верно и обратное: каждой точке
соответствует одна точка плоскости. Верно и обратное: каждой точке  плоскости можно поставить в соответствие комплексное число
плоскости можно поставить в соответствие комплексное число 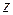 , действительная часть которого
, действительная часть которого 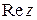 равна абсциссе точки, а мнимая часть
равна абсциссе точки, а мнимая часть 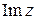 равна ординате точки. Таким образом, между комплексными числами и точками плоскости устанавливается взаимно однозначное соответствие. (Ранее мы говорили о взаимно однозначном соответствии между действительными числами и точками числовой прямой).
равна ординате точки. Таким образом, между комплексными числами и точками плоскости устанавливается взаимно однозначное соответствие. (Ранее мы говорили о взаимно однозначном соответствии между действительными числами и точками числовой прямой).
Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью. Для отличия её от действительной плоскости в правом верхнем углу пишут букву 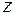 , обведенную кружком. Ось абсцисс на такой плоскости называют действительной осью, а ось ординат – мнимой осью. Комплексно-сопряженное число – это зеркальное отражение заданного комплексного числа относительно действительной оси. Начало координат называется нуль-точкой. Расстояние комплексного числа от начала координат называется модулем этого числа:
, обведенную кружком. Ось абсцисс на такой плоскости называют действительной осью, а ось ординат – мнимой осью. Комплексно-сопряженное число – это зеркальное отражение заданного комплексного числа относительно действительной оси. Начало координат называется нуль-точкой. Расстояние комплексного числа от начала координат называется модулем этого числа:
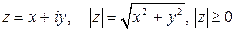 .
.
Модуль разности двух комплексных чисел – это расстояние между соответствующими точками:
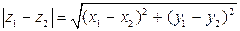 .
.
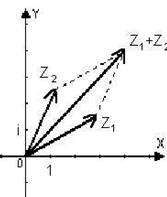
Каждой точке комплексной плоскости поставим в соответствие вектор с началом в нуль-точке и концом в данной точке. Очевидно, это соответствие взаимно однозначно. В такой интерпретации действительная и мнимая части комплексного числа – это первая и вторая компоненты вектора. Сумма 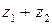 представляется теперь диагональю параллелограмма, построенного на векторах
представляется теперь диагональю параллелограмма, построенного на векторах 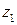 и
и 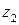 , разность
, разность 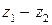 понимается как
понимается как 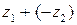 . Модуль комплексного числа представляет собой длину вектора. Геометрически очевидным является неравенство треугольника в комплексной плоскости:
. Модуль комплексного числа представляет собой длину вектора. Геометрически очевидным является неравенство треугольника в комплексной плоскости: 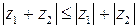 .
.
Пример 7. Указать геометрическое место точек на комплексной плоскости, для которых а) 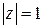 ; б)
; б) 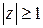 ; в)
; в) 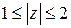 .
.
Решение. а) Модуль комплексного числа 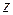 – это длина вектора, идущего из нуль-точки в точку
– это длина вектора, идущего из нуль-точки в точку 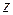 , т.е. расстояние от начала координат до точки
, т.е. расстояние от начала координат до точки 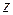 . Значит, в случае
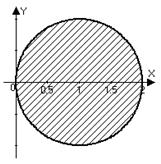
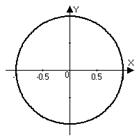
. Значит, в случае 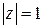 речь идет о геометрическом месте точек плоскости, равноудаленных от начала координат – это окружность (в данном случае радиус окружности равен 1). Можно было перевести задачу на язык декартовых координат:
речь идет о геометрическом месте точек плоскости, равноудаленных от начала координат – это окружность (в данном случае радиус окружности равен 1). Можно было перевести задачу на язык декартовых координат:
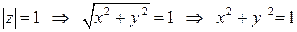 .
.
б) Здесь речь идет о геометрическом месте точек, находящихся вне круга радиуса 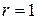 (с центром в начале координат).
(с центром в начале координат).
в) точки находятся в кольце между окружностями радиуса 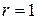 и
и 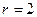 .
.
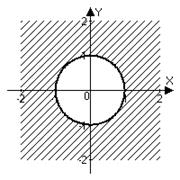
Пример 8. Указать геометрическое место точек на комплексной плоскости, для которых а) 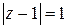 ; б)
; б) 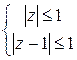 ; в)
; в) 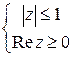 .
.
Решение. а) Модуль разности 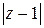 – это расстояние между точкой
– это расстояние между точкой 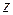 комплексной плоскости и точкой 1. Значит, речь идет о геометрическом месте точек, равноудаленных (на расстояние 1) от точки 1, – это окружность радиуса 1 с центром в точке (1;0). На языке координат:
комплексной плоскости и точкой 1. Значит, речь идет о геометрическом месте точек, равноудаленных (на расстояние 1) от точки 1, – это окружность радиуса 1 с центром в точке (1;0). На языке координат:
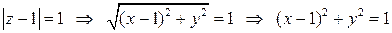 .
.
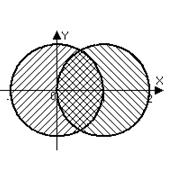
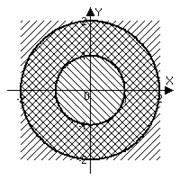
б) Точки находятся одновременно в круге 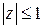 с центром в начале координат и в круге
с центром в начале координат и в круге 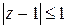 с центром, смещенным в точку
с центром, смещенным в точку 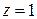 :
: 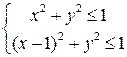 .
.
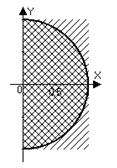
в) Это точки правой полуплоскости 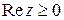 , лежащие внутри круга
, лежащие внутри круга 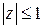 :
: 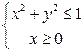 .
.
: