Тема 3
Центральное растяжение – сжатие стержня
Лекция №3
3.1 Внутренние усилия при растяжении и сжатии.
3.2 Дифференциальные зависимости между продольной силой и интенсивностью распределенной нагрузки.
3.3 Закон Гука при растяжении и сжатии.
3.4 Определение перемещений в общем случае растяжения и сжатия.
3.5 Обобщенный закон Гука.
3.6 Относительное изменение объема параллелепипеда.
3.7 Напряжения в сечениях, наклонных к оси стержня, при растяжении и сжатии.
Основные понятия.
Внутренние усилия при растяжении сжатии: Чистое центральное растяжение (ЧЦР), центральное растяжение (ЦР), правило знаков для продольной силы N, принцип Сен-Венана, гипотеза плоских сечений, выражение нормальных напряжений через продольную силу.
Дифференциальные зависимости между продольной силой и интенсивностью распределенной нагрузки.
Закон Гука при растяжении и сжатии: абсолютная и относительная деформации, коэффициент Пуассона.
Обобщенный закон Гука: формулы обобщенного закона Гука, относительное изменение объема параллелепипеда.
3.1 Внутренние усилия при растяжении и сжатии.
Рассмотрим стержень, по торцам которого приложены поверхностные силы интенсивность 
(рис. 3.1). Площадь поперечного сечения стержня 
. Равнодействующая внешних сил 
совпадает с осью стержня. Такой вид деформации стержня называется чистым центральным растяжением ( ЧЦР ).
Рис. 3.1 Чистое центральное растяжение (ЧЦР).
Если внешние силы распределены по торцам неравномерно (рис. 3.2), но приводятся к равнодействующей сливающейся с осью стержня, то такой вид деформации стержня называется центральным растяжением ( ЦР ).
Рис. 3.2 Центральное растяжение (ЦР).
При ЧЦР (ЦС) в поперечных сечениях стержня возникает только продольная сила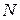 
.
Условимся: продольную силу считать положительной, если она вызывает растяжение, т.е. направлена от сечения, и отрицательной, если она вызывает сжатие, т.е. направлена к сечению.
Гипотеза плоских сечений: поперечные сечения стержня, плоские и перпендикулярные его оси до деформации, остаются плоскими и перпендикулярными оси и после деформации.
Из этой гипотезы следует, что все продольные волокна деформируются одинаково и нормальные напряжения, вызывающие эти деформации также должны быть одинаковыми и, следовательно, распределены по поперечному сечению равномерно, т.е. 
. С учетом формулы 
(см. (2.3)) получаем формулу для нормальных напряжений при ЧЦР:
 .
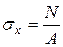| (3.1) |
Формула (3.1) справедлива и при центральном растяжении, но только в точках, находящихся на достаточном удалении от места приложения внешних сил (принцип Сен-Венана).
Экспериментальная проверка принципа Сен-Венана при центральном растяжении будет демонстрироваться при проведении лабораторной работы №17.
Пример 3.1 Определение внутренних усилий при растяжении и сжатии.
Рис. 3.3 Определение продольной силы на участках стержня.
Начало координат выбираем на свободном конце стержня. Стержень разбиваем на два участка. Проводим сечение 1-1 в произвольном месте 1-го участка и рассматриваем равновесие части стержня слева от проведенного сечения, определяем продольную силу 
из уравнения равновесия. Аналогично определяем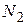 
.
1-й участок.  (рис. 3.3б)
  
| 2-й участок.  (рис. 3.3в)
 
|
На рис.3.4 показан график изменения продольной силы по длине стержня (эпюра). Заметим, что в точке приложения сосредоточенной силы эпюра продольных сил делает скачок равный по величине этой силе.
Рис. 3.4 Эпюра продольных сил.
Дифференциальные зависимости между продольной силой и интенсивностью распределенной нагрузки.
Рис. 3.5 Вывод дифференциальной зависимости между 
и .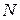
Обозначим - интенсивность распределенной нагрузки, действующей на стержень. Тогда уравнение равновесия элемента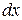 
стержня (
) примет вид: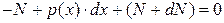 
. В результате получаем искомую дифференциальную зависимостьмежду продольной силой и интенсивностью распределенной нагрузки
 .
| (3.2) |
3.3 Закон Гука при растяжении и сжатии.
Рассмотрим чистое центральное растяжение стержня силами интенсивностью 
. Будем считать, что внешние силы вызывают в стержне только упругие деформации, т.е. после снятия нагрузки стержень принимает свою первоначальную форму и размеры.
Рис. 3.7 Продольные и поперечные деформации стержня.
Введем обозначения:
| абсолютная продольная деформация | относительная продольная деформация | относительная поперечная деформация | относительная поперечная деформация |
| 
| 
| 
|
На основе серии опытов со стержнями из различных материалов были установлены следующие положения закона Гука:
1) абсолютное удлинение стержня прямо пропорционально продольной силе 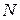, длине 
и обратно пропорционально площади поперечного сечения и модулю упругости материала стержня 
 .
| (3.3) |
2) относительная поперечная деформация прямо пропорциональна относительной продольной деформации
| (3.4) |
В формуле (3.4) 
- коэффициент Пуассона, безразмерная величина. Знак минус в формуле (3.4) означает, что если в направлении оси 
стержень испытывает деформации растяжения, то в направлении осей 
стержень испытывает деформации сжатия.
Таким образом, для каждого материала существует две упругие постоянные: -модуль упругости и коэффициент Пуассона .
Если обе части формулы (3.3) разделить на , а затем воспользоваться формулами для нормальных напряжений и относительных деформаций, то закона Гука можно записать в виде
| (3.5) |
Из формулы (3.5) следует, что модуль упругости имеет туже размерность, что и напряжение, т.е. 
.Например, для прокатной стали 
, 
.