Содержание
1. ВВЕДЕНИЕ....……………………………………………………………………3
2. О ВЕРОЯТНОСТИИ ТЕОРЕМЕ БАЙЕСА…………………………………....4
3. ПРИМЕНЕНИЕ ТЕОРЕМЫБАЙЕСА…………………………………………7
4. БАЙЕСОВСКИЕ МЕТОДЫМАШИННОГО ОБУЧЕНИЯ…………………..9
5. СПИСОК ИСТОЧНИКОВ……………………………………………………..12
Введение
Байесовская теория и байесовская вероятность названы в честь Томаса Байеса (1702—1761), доказавшего частный случай теоремы, сейчас называемой теоремой Байеса. Термин «байесовский» стал использоваться примерно в 1950 году, и большая часть того, что сейчас называется «байесовским», не имеет к Байесу прямого отношения. Лаплас доказал более общий случай теоремы Байеса и использовал её для решения задач небесной механики и медицинской статистики. Лаплас, однако, не считал эту теорему важной для развития теории вероятностей. Он придерживался классического определения вероятности.
О вероятности и теореме Байеса
На практике вероятность наступления события есть частота наступления этого события, то есть отношение количества наблюдений события к общему количеству наблюдений при большом (теоретически бесконечном) общем количестве наблюдений.
Рассмотрим следующий эксперимент: мы называем любое число из отрезка [0, 1] и смотрим за тем, что это число будет между, например, 0.1 и 0.4. Как нетрудно догадаться, вероятность этого события будет равна отношению длины отрезка [0.1, 0.4] к общей длине отрезка [0, 1] (другими словами, отношение «количества» возможных равновероятных значений к общему «количеству» значений), то есть (0.4 — 0.1) / (1 — 0) = 0.3, то есть вероятность попадания в отрезок [0.1, 0.4] равна 30%.
Теперь посмотрим на квадрат [0, 1] x [0, 1]

Допустим, мы должны называть пары чисел (X, Y), каждое из которых больше нуля и меньше единицы. Вероятность того, что X (первое число) будет в пределах отрезка [0.1, 0.4] (показан на первом рисунке как синяя область, на данный момент для нас второе число Y не важно), равна отношению площади синей области к площади всего квадрата, то есть (0.4 — 0.1) * (1 — 0) / (1 * 1) = 0.3, то есть 30%. Таким образом можно записать, что вероятность того, что X принадлежит отрезку [0.1, 0.4] равна p(0.1 <= X <= 0.4) = 0.3 или для краткости p(X) = 0.3.
Если мы теперь посмотрим на Y, то, аналогично, вероятность того, что Y находится внутри отрезка [0.5, 0.7] равна отношению площади зеленой области к площади всего квадрата p(0.5 <= Y <= 0.7) = 0.2, или для краткости p(Y) = 0.2.
Теперь посмотрим, что можно узнать о значениях одновременно X и Y.
Если мы хотим знать, какова вероятность того, что одновременно X и Y находятся в соответствующих заданных отрезках, то нам нужно посчитать отношение темной площади (пересечения зеленой и синей областей) к площади всего квадрата: p(X, Y) = (0.4 — 0.1) * (0.7 — 0.5) / (1 * 1) = 0.06.
А теперь допустим мы хотим знать какова вероятность того, что Y находится в интервале [0.5, 0.7], если X уже находится в интервале [0.1, 0.4]. То есть фактически у нас есть фильтр и когда мы называем пары (X, Y), то мы сразу отбрасывает те пары, которые не удовлетворяют условию нахождения X в заданном интервале, а потом из отфильтрованных пар мы считаем те, для которых Y удовлетворяет нашему условию и считаем вероятность как отношение количества пар, для которых Y лежит в вышеупомянутом отрезке к общему количеству отфильтрованных пар (то есть для которых X лежит в отрезке [0.1, 0.4]). Мы можем записать эту вероятность как p(Y|X). Очевидно, что эта вероятность равна отношению площади темной области (пересечение зеленой и синей областей) к площади синей области. Площадь темной области равна (0.4 — 0.1) * (0.7 — 0.5) = 0.06, а площадь синей (0.4 — 0.1) * (1 — 0) = 0.3, тогда их отношение равно 0.06 / 0.3 = 0.2. Другими словами, вероятность нахождения Y на отрезке [0.5, 0.7] при том, что X уже принадлежит отрезку [0.1, 0.4] равна p(Y|X) = 0.2.
Можно заметить, что с учетом всего вышесказанного и всех приведенных выше обозначений, мы можем написать следующее выражение
p(Y|X) = p(X, Y) / p(X)
Кратко воспроизведем всю предыдущую логику теперь по отношению к p(X|Y): мы называем пары (X, Y) и фильтруем те, для которых Y лежит между 0.5 и 0.7, тогда вероятность того, что X находится в отрезке [0.1, 0.4] при условии, что Y принадлежит отрезку [0.5, 0.7] равна отношению площади темной области к площади зеленой:
p(X|Y) = p(X, Y) / p(Y)
В двух приведенных выше формулах мы видим, что член p(X, Y) одинаков, и мы можем его исключить:
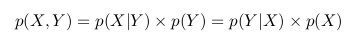
Мы можем переписать последнее равенство как
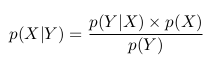
Это и есть теорема Байеса